1)Колебания - процесс характеризующийся периодической повторяемостью во времени.

Гармонические колебания это колебания которые совершаются по закону sin или cos.

Мы рассматриваем механические колебания потому что: (1) ряд процессов имеет гармонический характер. (2) Любой периодически процесс можно представить в виде суперпозиции суммы гармонических колебании.

Свободные колебании – колебании которые возникают в результате начального внешнего воздействия и дальнейшем отсутствии внешних воздействии.

Уравнение колебании - где - колеблющуюся величина (может быть каждый атом, ток, заряд и т.д). -амплитуда колебании (максимальное значение колеблющейся величины) -фаза колебании. начальная фаза колебании при .циклическая частота колебании.

период колебании это время одного полного колебания через которое система принимает начальное состояние при этом фаза колебании изменится на .. . Величина, обратная периоду колебаний, , т.е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний.

Комплексная форма колебании.

Т.к комплексное число можно задать в виде вектора или точки на графике где и . По теореме Эйлера . где .... Вещественная часть выражения представляет собой гармоническое колебание.

Метод вращающегося вектора.

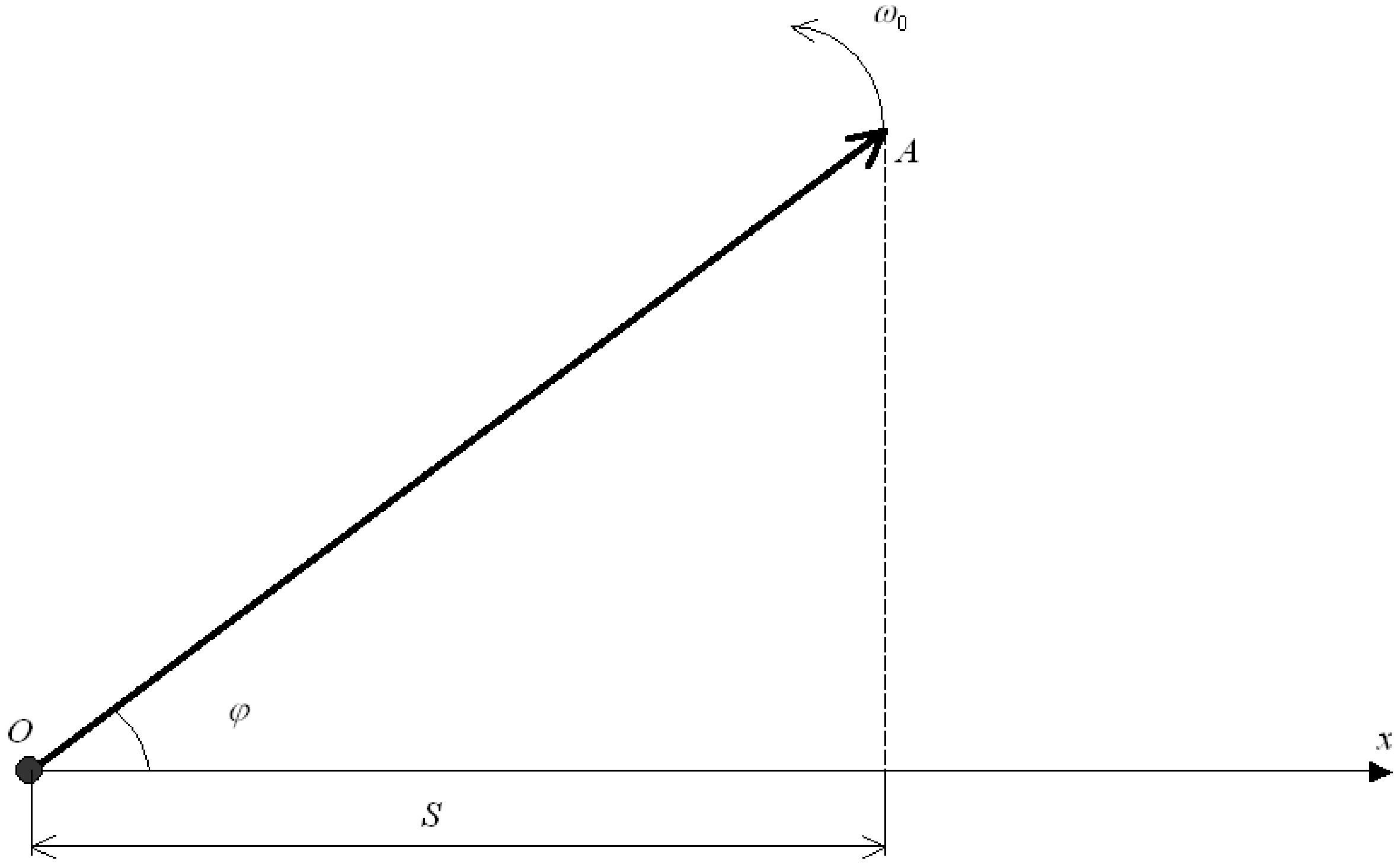Для этого из точки , выбранной на оси , под углом , равным начальной фазе, откладывается вектор , модуль которого равен амплитуде . Если этот вектор привести во вращение с угловой скоростью , то проекция конца вектора будет перемещаться по оси и принимать значения от до , а колеблющаяся величина будет изменяться со временем по закону . Таким образом, гармоническое колебание можно представить проекцией вектора амплитуды на произвольно выбранную ось.

Механические колебания.

Пусть материальная точка массой m колеблется вдоль оси х так что , видно что опережает по фазе координату на . амплитуда скорости. Ускорение опережает по фазе координату на .. Сила , действующая на колеблющуюся материальную точку массой , с учётом вышеуказанных выражений, равна . Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону (к положению равновесия).

Энергия гармонических колебании.

. . , . ..Полная механическая энергия свободных незатухающих гармонических колебании остается const и не зависит от t.

Гармонический осциллятор это система, совершающая колебательные движения, которые описываются дифференциальным уравнением.При рассмотрении колебании всех механических систем начинаем с записи 2-го закона Ньютона или основного закона вращательного движения и из них приходим к дифференциальному уравнению свободных гармонических колебании.

Ищем решение этого уравнения . ,теперь подставляем в первое уравнение. ,это так называемое характеристическое уравнение из него . ., . Подставляем в , т.е 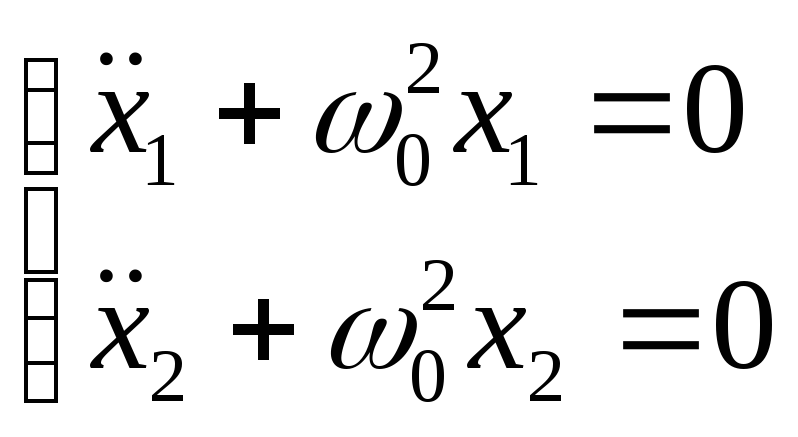значит ирешения уравнении тогда оба решения можно представить .. решение дифференциального уравнения колебании дифференциальное уравнение колебании.

Пружинный маятник – представляет собой тело массой m подвешенное на пружине жесткостью k и совершающее гармонические колебания под действием сил упругости. (рис.) Для того чтоб начались колебания нужно тело вывести из положения равновесия или толкнуть.

(рис.) сила уравновешивающая силу тяжести . дополнительная сила приводящая к колебаниям.

II закон Ньютона для обоих случаев:

1. , ,

2. , , ,. Знак минус показывает что сила направлена против смещения. , ,, обозначим -строго положительная величина. -дифференциальное уравнение свободных незатухающих колебании.

Решение: частота колебании. , .

Чем меньше масса груза тем меньше период колебании. Чем меньше жесткость пружины г тем больше период колебании. (Рис.)

Физически маятник - твердое тело совершающее колебания под действием сил тяжести. (рис.) О – ось вращения. Основной закон динамики вращательного движения . Рассмотрим движение к положению равновесия: ;;. От положения равновесия: ;;,,,Угол мал поэтому, вектор углового перемещения. Вращаем бур от положения равновесия в сторону увеличения угла, тогда поступательное движение бура показывает направление вектора углового перемещения. ,,Подставляем в основной закон динамики вращательного движения: ,;;. Обозначим т.к . дифференциальное уравнение свободных незатухающих колебании.

Решение: , частота колебании ;. приведенная длина физического маятника; - момент инерции твердого тела относительно оси вращения проходящего через точку О.

По теореме Штейнера. значит ;,точка качания. Если поменять местами ито период колебании не изменится. (Рис.)

Математический маятник – это тело подвешенное на нити длинной совершающее колебательные движения под действием силы тяжести. (рис.) Основной закон динамики вращательного движения ;, ;,.К положению равновесия:,. От положения равновесия: ,, ,,;,мал поэтому.вектор углового перемещения. Вращаем бур от положения равновесия в сторону увеличения угла, тогда поступательное движение бура показывает направление вектора углового перемещения.,, ,;,,;. Обозначаем ,,. дифференциальное уравнение свободных незатухающих колебании.

Решение: ,частота колебании, ;. Приведенная длина физического маятника это такая длина математического маятника при которой маятники колеблются синхронно. На частоту влияет длина нити. (рис.) качаем маятник под ним тянем платформу и в конце по картинке смотрим что он совершает гармонические колебания (рис.)

2)Затухающие колебания – это колебания амплитуда которых уменьшается с течением времени из-за потерь энергии реальной колебательной системы. В механической системе потеря энергии возникает из-за трения. Рассмотрим колебания пружинного маятника который находится в вязкой среде (глицерин). (рис.)

II закон Ньютона: , , ., сила вязкого трения пропорциональна скорости движения частицы. , ,,,.Обозначаем: ;. (1) дифференциальное уравнение свободных затухающих колебании.

При решении задач после дифференциальных уравнении надо записать его решение. Решать не надо. На теории решение - , ,,,.-характеристическое уравнение. ,т.е., Дифференциальное уравнение (1) имеет 2 решения: ;., ,.Подставляем: ;;Комплексное число равно 0 когда обе его части равны 0. ,.рациональные корни...,..,

Решение: , . Амплитуда колебании экспоненциально убывает со временем. (рис.)1. (рис.)2.

Поскольку амплитуда колебании уменьшается со временем то о периоде колебании говорить нельзя. Но при малых затуханиях . Декремент затухания отношение амплитуд колебании через период. .

Логарифмически декремент затухания это логарифм от отношения амплитуды через период. .

Время релаксации это время за которое амплитуда колебании уменьшается враз , ,. число полных колебании в течении которых амплитуда уменьшилась враз. ,,.

3)Вынужденные колебании.

Для того чтоб поддержать колебании в вязкой среде нужно компенсировать потери энергии, т.е на тело должна воздействовать внешняя вынуждающая сила изменяющиеся по гармоническому закону..

Для пружинного маятника: , ,. ,,. Обозначим , , дифференциальное уравнение вынужденных колебании. -частота внешней вынужденной силы. Решением неоднородного дифференциального уравнения сумма 2-х решении.

1. Общее решение: ,,

2.Частное решение: Заметим что , можно предположить что тогда дифференциальное уравнение вынужденных колебании можно записать для, (2), решением будет некоторое значение , значит . Решение ур-ния (2) в виде: , ,. Подставим в уравнение (2) т.к решение ур-ия должно выполняться при любом значении то , получим , , ,Решение дифференциального уравнения (2). ,,,,,, ,- амплитуда колебании.-фаза колебании, . Амплитуда и фаза вынужденных колебании зависят от частоты вынужденных колебании.

Проанализируем зависимость от частоты амплитуды и фазы колебании. .Амплитуда принимает при некотором значении максимальное значение., , сократим Частота при которой наблюдается максимум равен . .

При , .

,,.

при ,, при .

(рис.) В системе где возникают вынужденные колебания наблюдаются резонансные явления, при некоторой частоте внешней вынуждающей силы, амплитуда вынужденных колебании резко возрастает.

1. дифференциальное уравнение свободных незатухающих колебании

Решение: Начальная фаза и амплитуда колебании зависят от конкретных начальных условии. Если маятник вывести из положения равновесия сообщив потенциальную энергию то координата в момент

(1), .(2)Толкаем, .

.,. ;,.

2. свободных затухающих колебании.

Решение: , .

3. Вынужденные колебания, ,,.

4)Сложение 2-х гармонических колебании одного направления с близкими частотами (Биение). Пусть тело участвует в в 2-х колебаниях одного направления ,;;.Для (1) (2) ,.

,,,т.к то ; амплитуда результирующего колебания. период основных колебании. период колебании амплитуды. Т.кто .

(рис.)

Частота колебании в камертонах разная. Стучим по 2-м камертонам и идет биение колебания складываются!

Сложение 2-х гармонических колебании одинаковой частоты и направления. (рис.)

,. Представим эти колебания с помощью метода вращающегося вектора. Т.к. векторы и вращаются с одинаковой угловой скоростью , то разность фаз между ними остаётся постоянной. Тогда результирующий вектор будет зависеть от амплитуды и х -проекции результирующего вектора. . ,. Амплитуда результирующего колебания зависит от разности начальных фаз этих колебании..

1. Амплитуда принимает максимальное значение когда,,.

2.Принимает минимальное значение,

3.Если ,,

Сложение взаимно перпендикулярных колебании. (рис.)

Результирующая колебании приводит к тому что шар движется по определенной траектории.

, -разность фаз этих колебании. Т.к,то,;. Ур-ие эллипса ориентированно произвольным образом относительно оси координат. (рис.)

1. ,,.,,.

2.,,.,,

3. ,,.(рис.) ,(рис.)

Направление движения определяется вдоль окружности и зависит от . Если то движение по часовой стрелке, если то против. Маятник качаем потом его отклоняем так чтоб это отклонение было перпендикулярно прежнему в следствии его движения чего получаем эллипс.(рис.)