4.Циркуляция вектора напряженности электростатического поля.

Теорема о циркуляции (интегральная формулировка).

(рис 19) Пусть создает поле, тогда внесем в поле пробный заряди будем его перемещать, не в сторону действующей силы.- совершает работу:,,,,;. Работа не зависит от формы траектории, а зависит от начального и конечного положения.

Если заряд перемещается по замкнутому контуру, то .

,,циркуляция вектора напряженности по замкнутому контуру. Для электростатического поля. Циркуляция вектора напряженности электростатического поля по произвольному замкнутому контуру равна нулю. Теорема о циркуляции показывает, что линии электростатической напряженности не замкнуты, циркуляция равно нулю.

Дифференциальная формулировка теоремы о циркуляции.

следовательно электростатическое поле потенциально. Для определения потенциальности поля необходимо вычислить циркуляцию по замкнутому контуру. Иногда это громоздкая процедура поэтому ищем другой критерии потенциальности электростатического поля, им является дифференциальная формулировка. Дифференциальная формулировка определяется напряженностью поля в данной точке пространства.

Рассмотрим произвольный контур. Натянем на него площадку S. (рис 19)

Дальше должны стянуть этот контур в точку. При этом циркуляция ,,, а отношение, причем отношение определяется не только величиной но и направлением нормали к контуру. Положительную нормаль определим по правилу буравчика: вращательное движение совпадает с направлением обхода контура, поступательное движение показывает направление нормали.

принимает максимальное положительное значение для положительной нормали и отрицательное если меняется обход контура, т.е эта величина ведет себя как проекция некоторого вектора на направление нормали и называется ротором.

.

Выражение для в декартовой системе координат.

Для этого – определим циркуляцию по замкнутому контуру нормаль которого совпадает с направлением Ох.

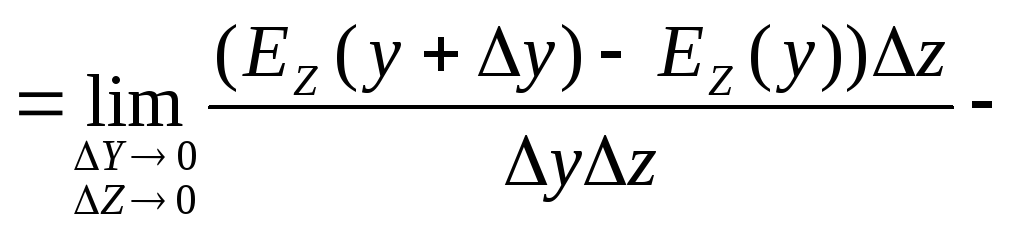
(рис 20) Выберем контур в виде прямоугольника. ,;. Аналогично и для Оу иOz и для определения проекции можно использовать правило циклических перестановок.

;.

Если известен в каждой точке поля, то можно найти циркуляциюпо произвольному замкнутому контуру. Для этого на контур натянута площадка и ее разбиваем на бесконечно малые элементыв этом случаесчитаем плоским.

По определению (рис 21) просуммируем циркуляции по всем контурам. Сумма циркуляции в соседних контурах равна нулю, потому что обходы разные, следовательно, при суммированииполучается циркуляция по замкнутому контуру.илипоток ротора вектора:

1) Если , то, посколькуверно для любой точки поля, то

2) Если , тозначит поле потенциально.

Критерием потенциальности поля является .

5.Потенциал электростатического поля.

Электростатическое поле потенциально, т.е можно ввести понятие потенциальности энергии и работа равна убыли потенциальной энергии: ;.

(рис 19) Пусть создает поле, тогда внесем в поле пробный заряди будем его перемещать, не в сторону действующей силы.- совершает работу:,,,,;. Работа не зависит от формы траектории, а зависит от начального и конечного положения.

Работа по перемещению заряда .

напряжение определяется с точностью до константы.

При заряды не взаимодействуют, т.е,

- это выражение не зависит от величины , является характеристикой поля создаваемого зарядом. Характеристику поля называютпотенциалом - это скалярная энергетическая характеристика поля равна потенциальной энергии единичного пробного заряда, помещенного в данную точку поля.

,, работа по перемещениюв поле с разностью потенциалов. Если заряд переместить из данной точки поля на бесконечность, то,.Потенциальная работа по перемещению заряда из данной точки на бесконечность. Вольт – потенциал точки поля в которой заряд 1 кулона обладает потенциальной энергией в 1 джоуль.

Если поле создается несколькими зарядами, то потенциал электростатического поля равен алгебраической сумме потенциалов создаваемых каждым зарядом в отдельности в данной точке поля.

Связь и.

1.Связь силы и потенциальной энергии.

,.

, ,.

2. ,;

, ,Аналогично для других компонентов.

,

Для удобства графического потенциала используем эквипотенциальные поверхности.

Эквипотенциальные поверхности – это поверхности равных потенциалов.

Покажем, что линии напряженности всегда перпендикулярны к эквипотенциальным поверхностям. Для этого определим работу по перемещению вдоль эквипотенциальной поверхности из точки 1 в точку 2.

,,,, т.к мы перемещаем.,,,

Очень удобно определять экспериментально потенциал зная распределение заряда. Если необходимо наитии напряженность в какой-то точке поля, то надо воспользоваться связьюитаким образом надо получит уравнение связывающеес.

Теорема Гаусса.

, ;;

;- уравнение Пуассона. Зная распределение зарядов можно найти разностьмежду точками иликаждой точки. Еслито. Знаяможно найти напряженность каждой точки..