2.Поле диполя.

Диполе – система 2-х зарядов одинаковых по величинам и противоположных по знаку. Прямая соединяющая эти заряды – ось диполя. Расстояние между этими зарядами много меньше чем расстояние до других заряженных тел.

(рис 7) - плечо диполя вектор соединяющий отрицательный и положительный заряды.

- дипольный момент.

Поле на оси диполя.

(рис 8) точка А находится на расстоянии от середины диполя на оси диполя.,,,

Учитывая что имеем,.

Напряженность поля созданное диполем на перпендикуляре к оси диполя.

(рис 9)

,Из подобия треугольников следует,,,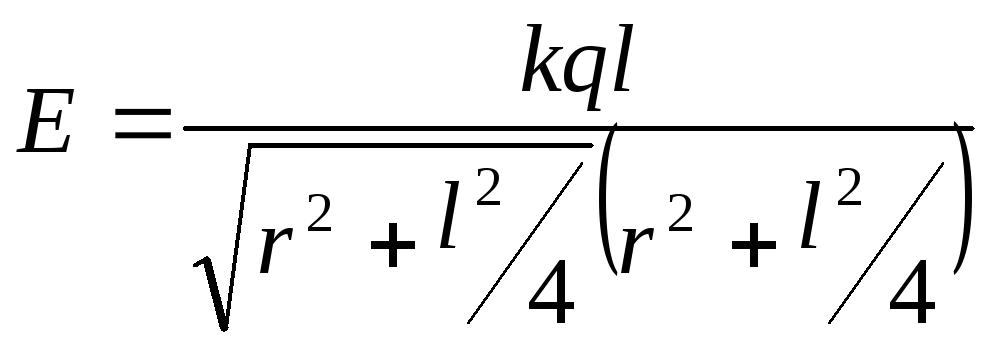 т.кто,.

Поведение диполя во внешнем поле.

Поле однородное.

(рис 10)

,,,,,,,,,. Согласно основному закону динамики вращательного движения ()т.к угловая скорость увеличивается тоследовательно диполь вращается по часовой стрелке. Когда диполь выстраивается по полю, т.е,поворот диполя прекращается.

Неоднородное электрическое поле

(рис 11)

Между точками игде находится заряд существует разница электрического поля.

, значит силы ,, под действиемдиполь будет поворачиваться по полю., то 1),значит поворачиваясь по полю диполь будет втягиваться в него.

2) поворачиваясь по полю диполь будет выталкиваться полем.

3.Поток вектора напряженности электростатического поля.

,, потоком вектора электростатического поля через бесконечно малую площадкуназывается скалярная величина равная скалярному произведению векторана,

, - нормаль площадки. (рис 12)

, если поверхность замкнута то поток через нее . Нормаль в случае замкнутой поверхности всегда берется внешняя (рис 13)

Теорема Гаусса для электростатического поля (интегральная формулировка).

. Поток вектора напряженности электростатического поля сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов находящихся внутри этой поверхности деленное на .

Если заряды распределены равномерно с объемной плотностью. ,тогда теорема Гаусса записывается.

Если с поверхностной плотностью. ,.

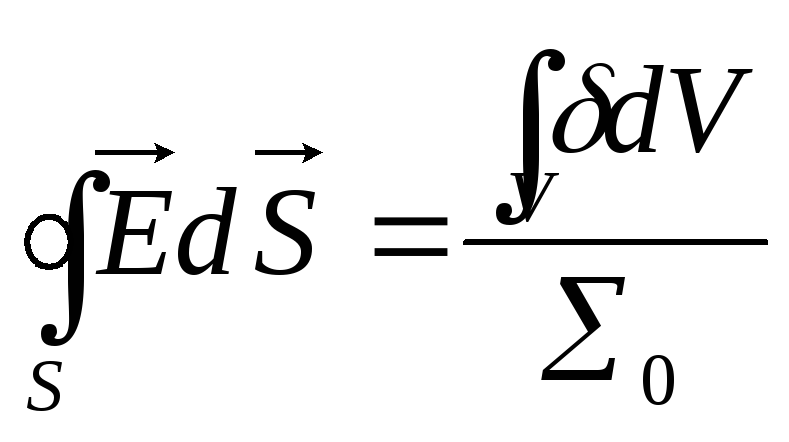Если линейная плотность заряда. ,.

Дифференциальная формулировка теоремы Гаусса.

Любая дифференциальная формулировка связывает две величины: объемную плотность заряда и напряженность электрического поля в окрестностях данной точки.

В интегральной формуле

Считаем, что заряд равномерно распределен по объему и среднее значение объемной плотности заряда равно .

Разделим левую и правую части выражения на объем охватываемый замкнутой поверхностью. , т.к площадь поверхности Гаусса стремиться к нулю значит поток. Но отношения потока вектора напряженности к объемустремится к некоторому пределу; При;,. По определениюназывается дивергенцией вектора. Дифференциальная формулировка.

Выражение для дивергенции в декартовой системе координат.

Для этого рассмотрим поток вектора напряженности через прямоугольный параллелепипед, ориентированный вдоль оси координат.

(рис 14) направлен произвольным образом.

- нормаль к передней грани вдоль Ох.

- нормально к задней грани против Ох.

- к правой боковой грани вдоль Оу

- к левой боковой против Оу

- к верхней грани вдоль Oz

- к нижней грани вдоль Oz

Поток через переднюю грань:

Через заднюю грань:

Через правую грань:

Через левую грань:

Через верхнюю грань:

Через нижнюю грань: .

По определению: ,.

Выражение для дивергенции в декартовой системе координат: .

По теореме Гаусса определяется поток через произвольную замкнутую поверхность. Поверхность выбираем таким образом чтоб было легче считать . Выбирают так чтобы части нормали были параллельны или перпендикулярны вектору.

1)1 случай. Поле бесконечное: равномерно заряженное с поверхностной плоскостью(), заряд распределен на плоскости. (рис 15)В качестве поверхности Гаусса выбираем цилиндр.

Рассмотрим левую часть .

Напряженность в каждой точке основания 1 одинакова в силу симметрии (основание параллельно заряженной поверхности) и в силу того что поверхность равномерно заряжена поэтому напряженность можно вынести за знак интеграла, аналогично с основанием 2.

Правая часть формулы. ,.

Все подставляем в теорему Гаусса: ,.Напряженность не зависит от координат точек, значит напряженность во всех точках поля одинакова – поле однородно.

2 случай.

(рис 16) ,,,,.

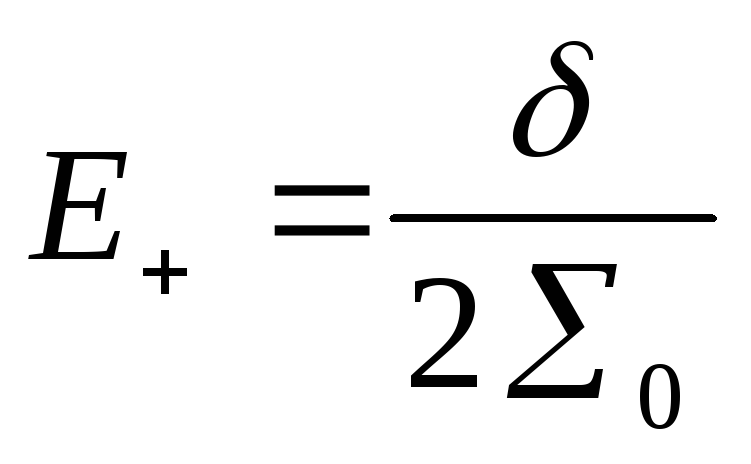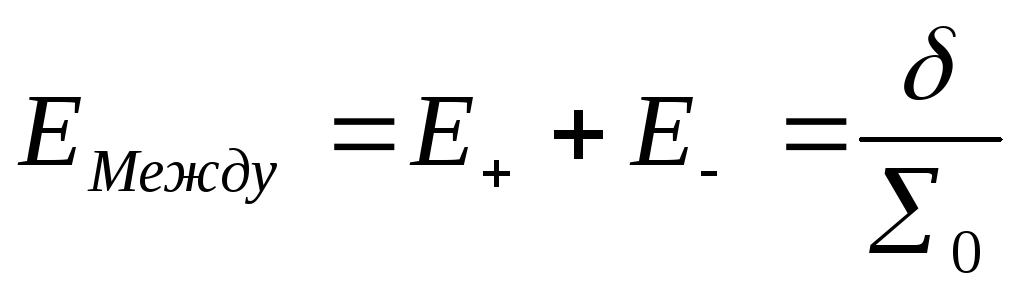2)Поле создаем шаром, R – заряженный объемной плотностью .

(рис 17) 1случай. Поверхность Гаусса сфера,r – радиус сферы.

Левая частьВ каждой точке поверхности Гаусса напряженность одинакова в силу симметрии и того что шар равномерно заряжен.

Правая часть: шар ..

Подставляем - поле не однородно.

2случай.(рис 18),. Заряд только на заряженном шаре.,.