Глава V. Элементы теории функций комплексной переменной
интегралы от аналитических функций вычисляются теми же методами, что и определенные интегралы в вещественном анализе.
Пример 2. |
|
Вычислить интеграл sinzdz , |
где AB - дуга окружности | z | = 1 |
AB |
|
от точки A: z1 = 1 до точки B: z2 = i |
в положительном направлении. |
Так как sin z - аналитическая функция на всем множестве C, то i
sinzdz = sin zdz cos z 1i = cosi cos1 cos1 ch1.
AB
1
Перейдем к рассмотрению интеграла другого частного ви-
да.
§9. Интеграл по контуру
Лекция 30
§9. Интеграл по контуру
Рассмотрим интеграл по контуру C. Для него, как и для интеграла по контуру от вещественной функции, используются обозначения:
Исследуем сначала свойства интеграла по контуру, которые описываются теоремами Коши.
1. Теоремы Коши
Теорема 1 (Теорема Коши для односвязной области).
|
|
Пусть функция f(z) |
аналитична в односвязной области D |
|
|
|
|
и C D - произвольный кусочно-гладкий контур. Тогда |
|
|
имеет место равенство |
|
|
|
|
|
|
|
|
|
|
f (z)dz 0 . |
|
(1) |
|
|
|
|
|
|
|
С |
|
|
|
|
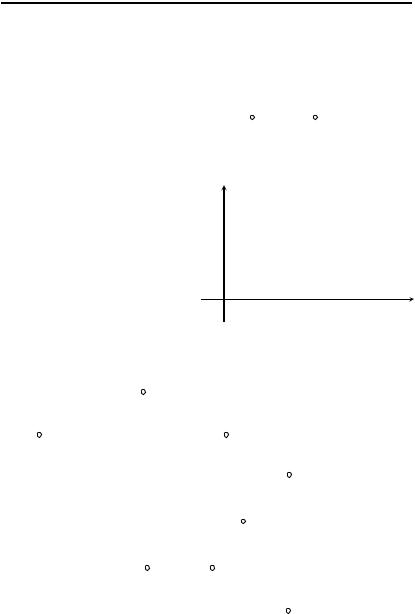
Доказательство. Возьмем произвольный контур |
C D, точки |
A, B на нем и вспомогатель- |
|
|
|
ные точки |
M, N. Имеют ме- |
y |
N |
|
сто равенства |
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
C |
AMB |
BNA |
AMB |
|
ANB |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как функция |
f(z) |
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
аналитична в области |
|
D, |
то |
|
|
|
согласно теореме 1 из §8 |
в O |
|
x |
этой |
|
|
области |
интеграл |
|
|
|
f (z)dz не зависит от формы пути интегрирования. Следова-
AB
Глава V. Элементы теории функций комплексной переменной
тельно, |
|
|
|
|
0 . Теорема доказана. |
► |
C |
|
AMB |
|
ANB |
|
|
Рассмотрим более сложную область.
Теорема 2 (Теорема Коши для многосвязной области).
Пусть C, C1 ,…, Cn - кусочно-гладкие контуры. Контуры C1 ,…, Cn лежат внутри контура C и вне друг друга. Об-
ласть D |
заключена между контуром |
C и контурами |
C1 ,…, Cn. |
Если при этом функция f(z) |
аналитична в об- |
ласти D и на всех контурах, то выполняется равенство |
|
n |
|
|
f (z)dz f (z)dz . |
(2) |
Сk 1 Сk
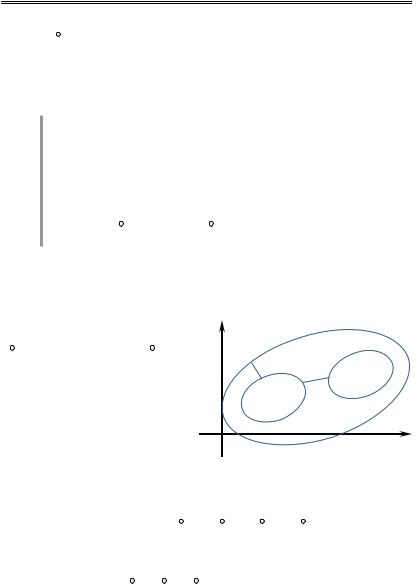
Доказательство рассмотрим для случая двух внутренних контуров. Пусть область D имеет вид. Проведем разрезы AB и EF области D. Область становится теперь односвязной. По предыдущей теореме получаем ра-
венство |
|
|
|
|
|
|
|
y |
|
C |
|
|
|
|
|
|
|
+ |
|
|
|
|
A |
|
|
C |
AB |
|
BME |
EF |
C2 |
|
|
|
M |
F |
+ |
|
|
|
0 . |
|
|
|
B |
E |
(*) |
|
|
|
|
|
|
|
C2 |
FE ENB |
BA |
|
|
|
|
|
|
C1 |
|
Согласно |
свойству |
1 |
|
N |
|
|
|
|
|
интеграла имеем: |
|
|
|
O |
|
|
x |
|
|
0 ; |
|
|
0 . |
|
|
|
|
AB |
BA |
|
|
EF |
FE |
|
|
|
|
|
|
|
Кроме того, выполняются равенства |
|
|
|
|
|
|
|
|
|
|
|
; |
|
. |
|
|
|
|
|
BME |
ENB |
C1 |
C1 |
C2 |
C2 |
|
Перенеся последние два интеграла в правую часть равенства (*),
получим равенство |
|
. Теорема доказана. |
► |
C |
C1 |
C 2 |
|
Что дает теорема? Сужение области, охватываемой контурfvb интегрирования.
Пример 1.
|
Вычислить интеграл |
|
dz |
|
z z0 |
|
|
|
|
С |
C - произвольный кусочногладкий контур, охватывающий
точку z0.
Прежде всего, отметим, что подынтегральная функция
1 |
|
|
f (z) |
z z |
0 |
аналитична в об- |
|
|
|
§9. Интеграл по контуру
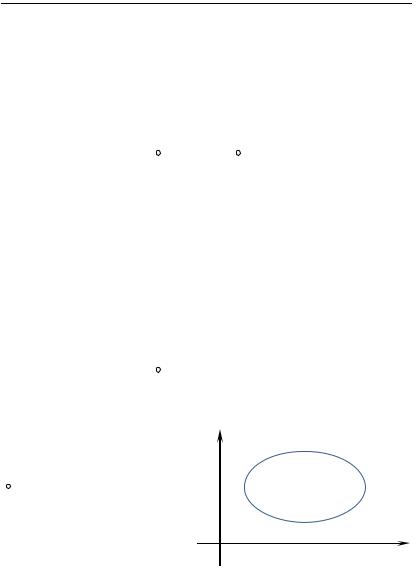
, где z0 - фиксированная точка и
y
|
ласти C \ {z0}. |
|
0 |
x |
|
Возьмем |
окружность |
|
|
|
|
C1: | z z0 | = R, |
лежащую |
|
|
|
внутри контура C. |
|
|
|
|
Рассмотрим область D, заключенную между контурами |
C и C1. |
Все условия теоремы 3 выполнены. Поэтому имеют место равенства:
|
dz |
|
|
dz |
|
2 i (см. пример 2 из §7.). Итак, |
|
dz |
|
2 i . |
z z |
0 |
z z |
0 |
z z |
0 |
С |
С1 |
|
С |
|
|
|
|
|
|
Идея стягивания контура к особой точке. Интеграл зависит от поведения функции только в малой окрестности особой точки.
2. Интегральное представление аналитических функций (Интегралы Коши)
 родолжим исследование интегралов по контуру.
родолжим исследование интегралов по контуру.
Теорема 3. Пусть односвязная область D ограничена кусочногладким контуром C. Пусть функция f(z) аналитична в области D и на контуре C. Тогда для всякой точки z D выполняется равенство
|
1 |
f (t)dt |
|
f (z) |
2 i C |
t z . |
(3) |
Доказательство. Рассмотрим вспомогательную функцию
Глава V. Элементы теории функций комплексной переменной
Пусть C1 - окружность с центром в точке z радиуса r, целиком лежащая внутри контура C. Тогда функция g(t) аналитична на контурах C, C1 и в области, заключенной между ними.
По теореме Коши получаем равенство g(t)dt g(t)dt .
С |
С1 |
1. Функция g(t) аналитична на контуре |
C и в области D |
за исключением точки z. В этой точке она даже не определена.
Однако, |
lim g(t) f |
(z) . До- |
y |
|
|
|
|
|
|
|
|
|
|
t z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определим g(t) по непрерыв- |
|
|
|
|
|
|
|
|
|
|
ности: |
g(z) f (z) . |
|
Теперь |
|
|
|
|
|
|
|
|
|
|
функция |
g(t) непрерывна и, |
|
|
|
|
|
|
|
|
|
|
следовательно, |
ограничена в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
замкнутой области |
|
D . Это |
|
|
|
|
|
|
|
|
|
|
означает, |
что |
существует |
0 |
|
|
|
|
|
|
|
|
x |
число M R, для которого |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| g(t) | < M. |
|
|
|
|
|
(*) |
2. Из неравенства (*) по свойству оценки интеграла полу- |
чаем |
неравенство | |
|
g(t)dt | M 2 r . Из |
него следует, что |
|
|
|
|
|
С1 |
|
|
|
|
|
|
|
|
|
|
|
|
lim | g(t)dt | 0 . Но тогда и |
lim |
g(t)dt 0 . Однако, интеграл |
r 0 С |
|
|
|
|
|
|
|
r 0 |
С |
|
|
|
|
|
|
от радиуса окружности не зависит. Поэтому |
g(t)dt 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
Итак, мы получили равенство |
f (t) f (z) |
dt 0 . Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
t z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вытекает |
равенство |
|
|
f (t) |
dt |
|
f (z) |
dt 0 |
. |
|
Второй интеграл |
|
|
|
|
|
|
|
|
|
С |
t z |
С |
t z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( z) |
был фактически вычислен в примере из §7: |
|
|
dt 2 i f (z) . |
|
t z |
С

|
|
§9. Интеграл по контуру |
Отсюда следует равенство |
f (t ) |
dt 2 i f (z) . Из данного ра- |
|
t z |
С |
|
|
венства вытекает равенство (3). |
► |
Равенство (3) называется интегральной формулой Коши,
а интеграл в правой части этого равенства - интегралом Коши.
Замечание 1. Из равенства (1) следует, что
значения аналитичекой функции в области полностью определяются ее значениями на границе этой области.
Перепишем равенство (3) в таком виде:
|
f (z) |
dz |
dt 2 i f (z0 ) . |
(4) |
|
z z0 |
|
С |
|
|
|
|
|
|
где функция f(z) аналитична в области DC, z0 DC.
Замечание 2. Интегральная формула Коши в виде (4) используется для вычисления интегралов по контуру.
Пример 2.
|
|
|
|
|
|
|
|
e |
z |
dz |
|
Вычислить интеграл |
|
|
|
|
. |
|
|
|
|
z 4 |
|
|
|
|
|
|
|
|z 5| 2 |
|
|
|
Функция |
|
f (z) ez |
аналитична в области DC : | z |
5 | 2, |
z0 = 4 |
DC. Кроме того, |
f (z ) f (4) e4 . Согласно равенству (4) |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
e |
z |
|
dz |
|
4 |
|
|
|
|
|
получаем |
|
|
|
2 ie |
|
. |
|
|
|
|
|
|
z 4 |
|
|
|
|
|
|z 5| 2
 ассмотрим теперь более общую ситуацию. Пусть функция f(z) определена и непрерывна на кусочно-гладкой кривой L. По аналогии с интегралом Коши рассмотрим интеграл
ассмотрим теперь более общую ситуацию. Пусть функция f(z) определена и непрерывна на кусочно-гладкой кривой L. По аналогии с интегралом Коши рассмотрим интеграл
1 f (t )dt . Он задает функцию
2 i L t z
g(z) |
1 |
|
f (t )dt |
, |
(5) |
2 i |
t z |
|
|
L |
|
|
|
определенную для любой точки z L.

Глава V. Элементы теории функций комплексной переменной
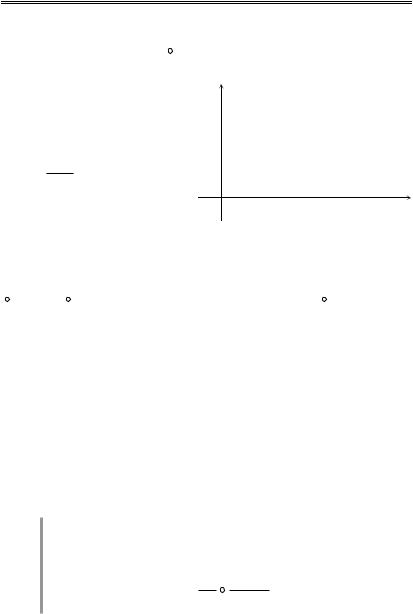
Интеграл (5) называется интегралом типа Коши.
|
Основное |
свойство |
y |
|
|
этого интеграла |
выражает |
L |
|
|
|
следующее утверждение. |
|
|
|
|
|
|
D |
|
|
|
O |
x |
Теорема 4. Функция g(z), определяемая интегралом типа Коши,
|
аналитична во всякой односвязной области |
D, не пересе- |
|
|
кающейся с кривой L. |
|
|
|
|
|
|
|
|
Функция g(z) имеет в области |
D производные любого |
|
порядка n, определяемые равенством |
|
|
|
(n) |
|
n! |
f (t )dt |
|
|
g |
|
(z) |
|
|
|
|
|
. |
(6) |
|
2 i |
|
|
n 1 |
|
|
|
|
|
L (t z) |
|
|
|
Доказательство опустим. |
|
|
|
|
|
|
|
|
Следствие. Функция f(z), аналитическая в односвязной области D и на ее границе C, имеет в данной области производные любого порядка n, определяемые равенством
|
(n) |
|
n! |
f (t)dt |
|
f |
|
(z) |
|
|
|
|
. |
(7) |
|
2 i |
(t z) |
n 1 |
|
|
|
|
C |
|
|
|
Доказательство. Равенство (7) вытекает непосредственно из равенства (6). Действительно, если кривая L является контуром C, то по теореме 3 выполняется равенство g(z) = f(z).
Перепишем равенство (7) в таком виде:
f (z) |
dz |
|
2 i |
f (n) (z0 ) , |
(8) |
|
n 1 |
C |
(z z0 ) |
|
n! |
|
|
|
|
|
|
где функция f(z) аналитична в области DC, z0 DC.
Замечание. Формула (8) используется для вычисления интегралов по контуру.
Пример 3.
sin z
Вычислить интеграл 2 2 dz .
| z| 3 (z 2)
Функция f (z) sin |
|
z |
аналитична в |
области |
DC : | z | < 3, |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
z0 = 2 DC, n = 1 . Так как |
f |
|
|
|
|
|
|
|
|
(z) 2 cos |
2 z , то согласно равенству (8) |
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin z |
|
2 i |
|
|
|
|
|
2 |
2 |
|
|
f (2) 2 i |
|
|
|
= |
|
|
|
|
cos( |
|
2) i . |
(z 2) |
2 |
1 |
|
|
2 |
2 |
| z| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
На этом мы закончим краткое знакомство с функциями комплексной переменной.




 родолжим исследование интегралов по контуру.
родолжим исследование интегралов по контуру.

 ассмотрим теперь более общую ситуацию. Пусть функция
ассмотрим теперь более общую ситуацию. Пусть функция 
