Мера различий: Метрики (расстояния)
Примеры различных метрик:
Мера различий: Метрики (расстояния)
Примеры различных метрик:
Мера различий: Метрики (расстояния)
Примеры различных метрик:
Композиция метрик:
Мера различий: Метрики (расстояния)
*Обобщения понятия метрики:
Мера различий: Метрики (расстояния)
*Обобщения понятия метрики:
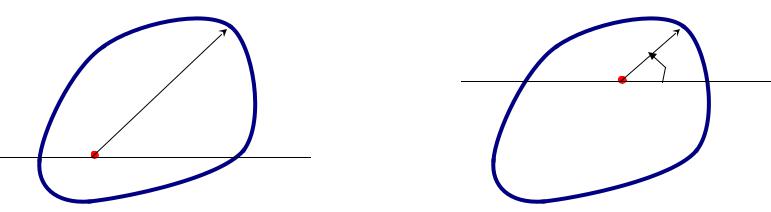
Мера различий: Метрики (расстояния)
*Обобщения понятия метрики:
Рассмотрим множество точек на плоскости со следующей квазиметрикой. Пусть задана некая выпуклая фигура (структурирующий элемент) S с полюсом O, граница которой S не содержит полюс и описывается в ее собственных полярных координатах непрерывной циклической функцией (переменным радиусом) rS( ), [0,2 ).
Размером фигуры S назовем максимальное значение ее радиуса r(S). Фигуру с центром O и размером r будем обозначать S(O,r).
Эксцентриситетом e(S) фигуры S назовем максимальное отношение
rS( )/rS( - ), [0,2 ).
Определим квазирасстояние dS(A,B) как размер r такой фигуры S(A,r), которая касается точки B: B S(A,r).
S |
S |
rS( ) |
rS( ) |
|
|
|
O |
O
Мера различий: Метрики (расстояния)
*Обобщения понятия метрики:
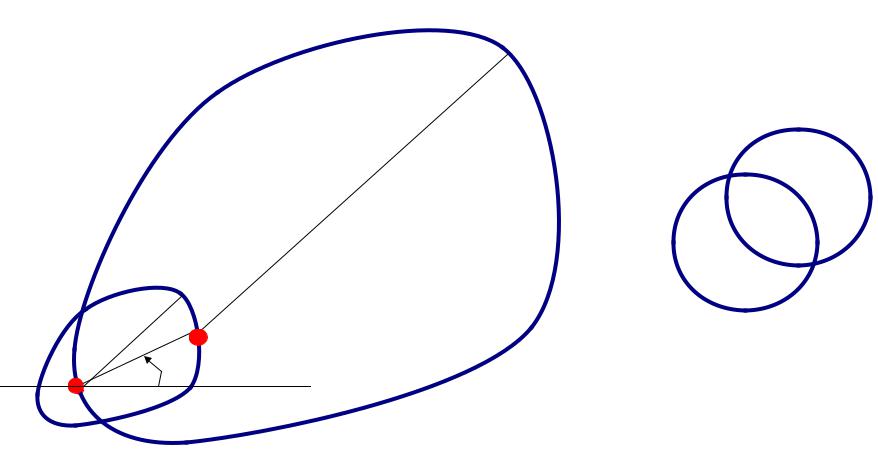
Свойства квазирасстояния dS(A,B)
1)dS(A,B) 0, dS(A,B) = 0 A = B
2)dS(A,B) e(S) dS(B,A), 1 e(S) <
3)dS(A,B) + dS(B,C) dS(A,C)
dS(B,A)
dS(A,B)
|
d(A,B) |
|
B |
|
|
A |
|
Частный случай – круговая фигурная квазиметрика совпадает с центрально симметричной евклидовой метрикой e(S)=1.
B
A 
d(A,B) = dS(A,B) rS( BA) = dS(B,A) rS( AB)
Напоминание:
Векторы и Линейные пространства
Вектор
Векторное пространство
Два вектора u, v и вектор их суммы
Определение: "Вектор" это такой математический объект, для которого определены операции сложения векторов и умножения вектора на число.
Примечание: Как и "чисел", "векторов" в математике множество. Например, функции также образуют векторное пространство.
Мера различий: Метрики (расстояния)
Метрики в нормированных линейных пространствах
Мера различий: Метрики (расстояния)
Метрики в нормированных линейных пространствах