
- •КОМПЬЮТЕРНЫЕ МЕТОДЫ ОБРАБОТКИ ИНФОРМАЦИИ
- •Содержание лекции
- •Задача сопоставления данных
- •Преобразования и эквивалентность
- •Преобразования и эквивалентность
- •Преобразования и эквивалентность
- •Преобразования и эквивалентность
- •Преобразования и эквивалентность
- •Преобразования и эквивалентность
- •Преобразования и эквивалентность
- •Преобразования и эквивалентность
- •Преобразования и эквивалентность
- •Преобразования и инварианты
- •Признаковое описание изображений
- •Признаковое описание изображений
- •Признаковое описание изображений
- •Признаковое описание изображений
- •Признаковое описание изображений
- •Признаковое описание изображений
- •Сопоставление данных как оценка степени связи и степени сходства
- •Статистическая корреляция
- •Ковариация
- •Коэффициент корреляции
- •Коэффициент корреляции
- •Коэффициент детерминации
- •Коэффициент детерминации
- •Взаимная информация
- •Измерение степени связи однотипных объектов
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Напоминание:
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Мера различий: Метрики (расстояния)
- •Меры сходства
- •Теоретико-множественные меры сходства
- •Меры сходства на основе скалярного произведения
- •Меры сходства на основе скалярного произведения
- •Нормированная линейная корреляция
- •Нормированная линейная корреляция
- •Нормированная линейная корреляция
- •Меры сходства и меры различия
- •Меры сходства и меры различия
- •Информационный поиск
- •Информационный поиск
- •Оценка эффективности поиска
- •Информационный поиск: индексы и алгоритмы
- •Поиск по ключевым словам
- •Поиск по ключевым словам
- •Алгоритмы нечеткого поиска
- •Алгоритмы нечеткого поиска
- •Дерево поиска
- •Красно-черное дерево поиска
- •Корреляционное обнаружение и прослеживание объектов на изображениях
- •Корреляционное обнаружение и прослеживание объектов на изображениях
- •Корреляционное обнаружение объектов на изображениях
- •Корреляционное прослеживание объектов на видеопоследовательностях
- •Корреляционное прослеживание объектов на видеопоследовательностях
- •Корреляционное прослеживание объектов на видеопоследовательностях
- •Корреляционное прослеживание объектов на видеопоследовательностях
- •Корреляционное прослеживание объектов на видеопоследовательностях
- •Корреляционное прослеживание объектов на видеопоследовательностях
- •Корреляционное прослеживание объектов на видеопоследовательностях
- •Корреляционное стерео отождествление (stereo matching)
- •Корреляционное стерео отождествление (stereo matching)
- •Корреляционное стерео отождествление (stereo matching)
- •Корреляционное стерео отождествление (stereo matching)
- •Корреляционное стерео отождествление (stereo matching)
- •Корреляционное стерео отождествление (stereo matching)
- •Стерео отождествление на основе характерных черт
- •Стерео отождествление на основе характерных черт
- •Стерео отождествление на основе характерных черт
- •Морфологическая корреляция Пытьева
Статистическая корреляция
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или
более переменными. При этом переменные могут быть разного типа (разной размерности, разной природы).
Корреляция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин.
При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.
Математической мерой корреляции двух случайных величин служит
коэффициент корреляции.
Отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент
корреляции будет отрицательным.
Положительная корреляция — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин.
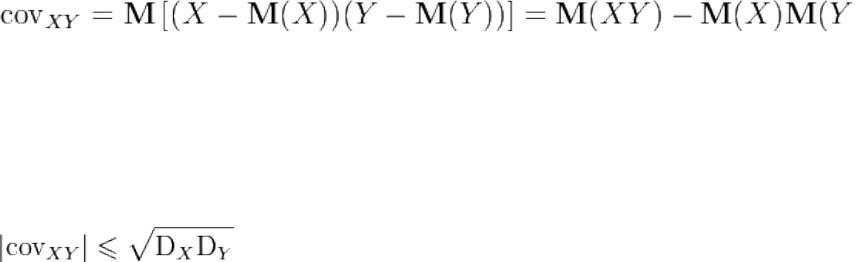
Ковариация
Ковариация (или корреляционный момент) является совместным центральным моментом второго порядка.
Ковариация определяется как математическое ожидание произведения отклонений случайных величин
где M — математическое ожидание.
Свойства ковариации:
Ковариация двух независимых случайных величин X и Y равна нулю., Абсолютная величина ковариации двух случайных величин X и Y не превышает среднего геометрического их дисперсий:
Ковариация имеет размерность, равную произведению размерности
случайных величин, то есть величина ковариации зависит от единиц измерения независимых величин. Данная особенность ковариации затрудняет её использование в целях корреляционного анализа

Коэффициент корреляции
Линейный коэффициент корреляции
Свойства коэффициента корреляции
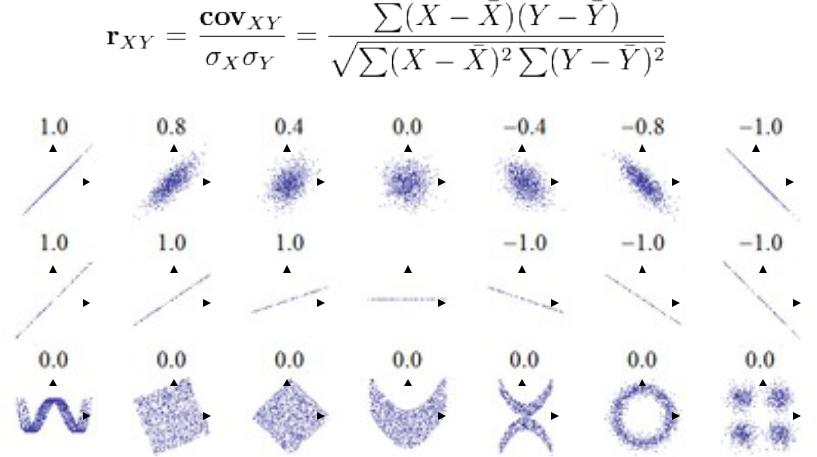
Коэффициент корреляции
Линейный коэффициент корреляции
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
Y |
|
|
X |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка).

Коэффициент детерминации
Линейная регрессия: 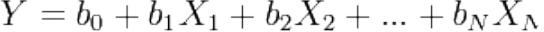 +
+
Коэффициент детерминации ( - R-квадрат) — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью зависимости (регрессии), то есть объясняющими переменными. Более точно — это единица минус доля необъяснённой дисперсии
(дисперсии случайной ошибки модели, или условной по факторам дисперсии зависимой переменной) в дисперсии зависимой переменной.
Его рассматривают как универсальную меру связи одной случайной величины от множества других.

Коэффициент детерминации
В частном случае линейной зависимости 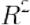 является квадратом так называемого множественного коэффициента корреляции между зависимой
является квадратом так называемого множественного коэффициента корреляции между зависимой
переменной и объясняющими переменными.
В частности, для модели парной линейной регрессии коэффициент детерминации равен квадрату коэффициента корреляции между y и x.
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это
интерпретируется как соответствие модели данным. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50% (в этом случае коэффициент множественной корреляции превышает по модулю 70%).
Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими (коэффициент корреляции превышает 90%). Значение коэффициента детерминации 1 означает функциональную зависимость между переменными.

Взаимная информация
Взаимная информация — статистическая функция двух случайных величин, описывающая количество информации, содержащееся в одной случайной величине относительно другой. Взаимная информация определяется через энтропию и условную энтропию двух случайных величин как
Свойства взаимной информации:
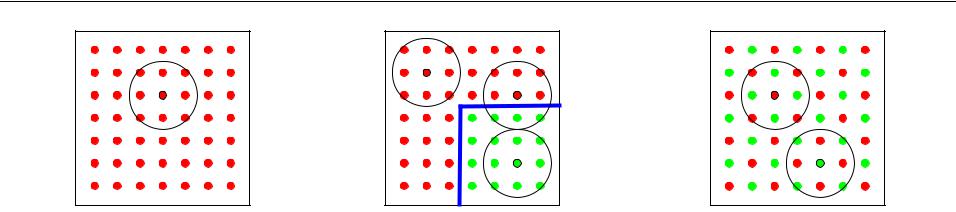
Измерение степени связи однотипных объектов
При оценке сходства/различия объектов одного типа (одной размерности, одной природы) их можно рассматривать как элементы какого-либо метрического пространства.
Принцип компактности: более близкие в метрическом смысле объекты должны с большей вероятностью иметь большее сходство и меньшее различие (принадлежать к одному классу эквивалентности).
Айзерман М. А., Браверман Э. М., Розоноэр Л. И. Метод потенциальных функций в теории обучения машин. М.: Наука, 1970. 320 pp.
компактный класс локально компактные классы |
некомпактные классы |
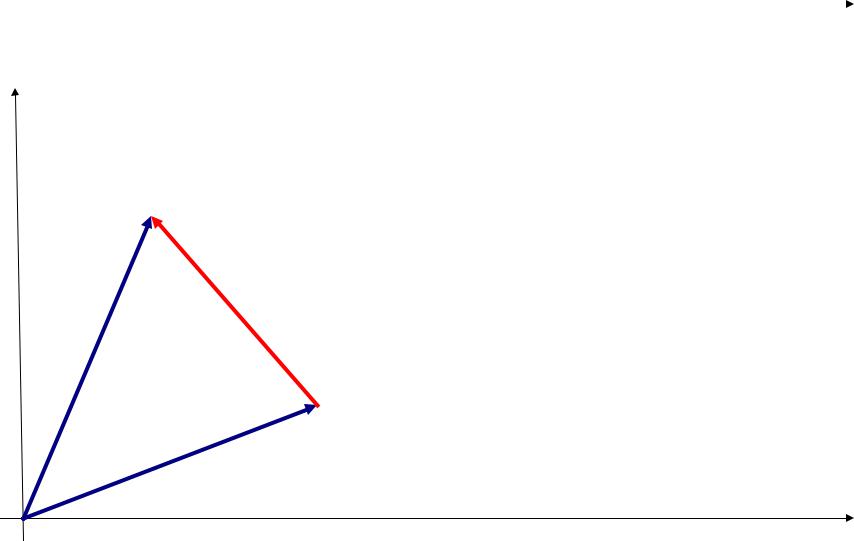
Мера различий: Метрики (расстояния)
|
|
|
|
|
x |
||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|||
a |
b d(a,b) = | b – a | |
||||||
y |
|
|
|
|
|
||
A |
|
d(a,b) = | b – a | |
|||||
|
|
|
|
|
|||
|
|
b – a |
|
|
|||
a |
|
|
|
|
|
||
d(a,b) = (x -x |
)2+(y -y )2 |
||||||
|
|
||||||
|
|
|
|
a b |
a b |
||
|
B |
b |
x |
|

Мера различий: Метрики (расстояния)
y
x |
z |
