Лекции по химии

23

цией (фотохимические, радиационно-химические и т.п.), в которых существенную роль играет воздействие излучений, однако и здесь определяющим является прежде всего механизм процесса.

Механизм химической реакции любой сложности может быть представлен совокупностью элементарных химических превращений, одностадийных реакций, которые называются простыми химическими реакциями. Для каждой из этих стадий можно записать кинетическую схему, которая напоминает стехиометрическое уравнение реакции, но подразумевает только одно направление: от реагентов – к продуктам реакции:

∑νiAi → ∑ν jBj

исх прод

2.1. Зависимость скорости реакции от концентрации

Закономерности влияния концентрации реагирующих веществ на скорость реакции для простых химических реакций сформулировали К. Гульдберг и П. Вааге по аналогии с законом действующих масс, известным из термодинамического описания положения химического равновесия.

Скорость простой химической реакции при постоянной температуре пропорциональна произведению концентраций реагирующих веществ, взятых в степенях, равных соответствующим стехиометрическим коэффициентам в уравнении реакции.

В соответствии с этим скорость простой химической реакции при постоянной температуре определяется соотношением:

v = k∏[Ai ]ν i .

исх

Здесь k – константа скорости химической реакции. Константа скорости реакции численно равна скорости реакции при единичных концентрациях реагентов. Таков физический смысл константы скорости (или удельной скорости реакции, как ее иногда называют). Величина k зависит от всех факторов, которые влияют на скорость реакции, за исключением концентраций реагентов.

В общем случае, когда реакция не является простой, показатель степени в формулировке Гульдберга и Вааге не совпадает со

24

стехиометрическим коэффициентом и представляет собой некий кинетический параметр процесса, называемый кинетическим порядком реакции по данному компоненту. Тогда идеализированное выражение из закона действующих масс трансформируется в

основной постулат химической кинетики:

v = k ∏[Ai ]ni .

исх

Здесь ni – кинетический порядок реакции по i-му компоненту. Сумма всех ni дает общий кинетический порядок реакции.

Порядок реакции и молекулярность. В случае сложных реакций порядок совпадает со стехиометрическим коэффициентом только для каждой стадии в отдельности. Для каждой элементарной стадии можно, в соответствии со стехиометрическим уравнением, определить количественное соотношение между реагентами и считать, что это соотношение соответствует числу реально участвующих в элементарном акте химического превращения частиц. Это число называется молекулярностью про-

цесса. Очевидно, что порядок реакции в общем случае не совпадает с её молекулярностью. Кинетический порядок определяется только экспериментально и может быть не только целым, но дробным, нулевым или даже отрицательным. Порядок реакции может не совпасть с молекулярностью даже для простой реакции! Предположим, нас интересует некая простая химическая реакция, протекающая по схеме A + 2B → C . Мы можем утверждать, что молекулярность её равна 3 и общий кинетический порядок составляет тоже 3. Однако, если мы вещество A возьмем в большом избытке по сравнению со стехиометрическим соотношением, то его концентрация в процессе реакции будет изменяться незначительно. Пренебрегая этим изменением и считая концентрацию [A] величиной постоянной, мы обнаружим, что n=2, т.к. на скорость процесса влияет только [B], а эта величина входит в выражение основного постулата химической кинетики для данной реакции во второй степени:

v = k[A] [B]2 .

Если в избытке окажется вещество B, то кинетический по-

25

рядок этой реакции n=1.

Кинетический порядок реакции и величину константы скорости можно определить экспериментально, исследуя зависимость концентраций компонентов в процессе химической реакции от времени. Такое исследование позволяет получить кинетические кривые данной реакции, из которых – математическими методами – можно рассчитать кинетические параметры процесса.

Рассмотрим кинетику процесса первого порядка, для которого выражение основного постулата химической кинетики записывается следующим образом:

v = kC .

Здесь C – концентрация реагента. Поскольку для реагента скорость реакции отрицательна, то

v = − dCdt .

В результате мы получаем дифференциальное уравнение с разделяющимися переменными:

− dCdt = kC .

Преобразовав это уравнение так, чтобы обе переменные находились в разных частях уравнения и учитывая граничные условия (в начальный момент времени t=0 исходная концентрация реагента составляет C0), можно проинтегрировать его

получив следующее решение для зависимости текущей концентрации реагента от времени:

C = C0e−kt .

Это уравнение и соответствует кинетической кривой реакции первого порядка. Для того, чтобы определить из экспериментальной зависимости значение константы скорости, существует довольно простой и эффективный прием: уравнение преобразуется в уравнение прямой вида y = a + bx .

27

то нетрудно убедиться, что константа равновесия в этом случае окажется равной отношению констант скоростей прямой и обратной реакций. Строго говоря, это неверно, поскольку в кинетической трактовке константа равновесия не оказывается безразмерной величиной, в отличие от определяемой термодинамически. Однако, в частном случае равновесия простой обратимой реакции численные значения действительно совпадают. Отметим, что концентрации компонентов, находящихся вне фазы, в которой протекает химическая реакция, в выражение закона действующих масс не входят, влияя только на величину константы равновесия.

Положение равновесия химической реакции, как и любого термодинамического равновесия, можно смещать внешними воздействиями. Правила смещения химического равновесия при внешних воздействиях основаны на известном термодинамическом принципе Ле Шателье – Брауна: внешнее воздействие, вы-

водящее систему из состояния термодинамического равновесия, вызывает в системе процессы, стремящиеся ослабить эффект воздействия. Так, при нагревании системы равновесие смещается в направлении эндотермических процессов, при повышении давления компоненты системы стремятся занять меньший объем, добавление какого-либо из компонентов вызывает его расходование в химической реакции.

2.2. Зависимость скорости реакции от температуры.

Температурная зависимость скорости химической реакции была впервые установлена Я. Вант-Гоффом, сформулировавшим эмпирическое (т.е., обобщающее опытные данные) правило:

T2 −T1 v(T2 ) = v(T1) γ 10 ,

где v(T1) и v(T2) – скорости реакции при соответствующих тем-

28

пературах, а γ – температурный коэффициент скорости, лежащий

для большинства известных химических реакций в интервале

2 ≤γ ≤ 4.

Таким образом, оказывается, что при повышении температуры на 10 К скорости подавляющего большинства реакций увеличиваются в 2 – 4 раза. В то же время известно, что при таком повышении в условиях, близких к нормальным, скорости движения молекул и частота их столкновений увеличивается в лучшем случае на доли процента. В чем же причина такой сильной температурной зависимости скорости химической реакции?

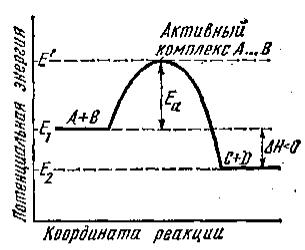
Не всякое столкновение частиц приводит к химическому превращению. Для того, чтобы это произошло, частицам необходимо преодолеть силы отталкивания и иметь энергию, достаточную для разрыва химических связей между образующими их атомами, только в этом случае возможно образование новых связей. Иными словами, для протекания химического превращения существует энергетический барьер (см. рис. 1). Высота этого барьера определяется химической природой реагирующих час-

тиц и называется энергией активации химической реакции.

Рис 1. Энергетическая диаграмма экзотермической химической реакции. Активный комплекс (переходное состояние) соответствует вершине потенциального барьера.

Энергия активации – характеристика конкретной химической реакции. Частицы, обладающие энергией, равной или большей энергии активации, становятся «активными», то есть, способными при столкновении вступить в химическую реакцию (активное столкновение). Число активных столкновений ZА, соглас-

29

но молекулярной статистике Больцмана, можно определить из соотношения:

− Ea

ZA = Z0 e RT ,

где Z0 – общее число столкновений, Ea – энергия активации, Т – абсолютная температура и R – универсальная газовая постоянная. Это соотношение позволяет вывести уравнение Аррениуса, строго описывающее (в отличие от правила Вант-Гоффа) температурную зависимость скорости химической реакции:

− Ea k = A e RT ,

где k – константа скорости реакции и A – предэкспоненциальный множитель, определяемый общей частотой столкновений и пространственным расположением молекул при столкновении.

2.3.Примеры решения задач.

1.Для обратимой химической реакции 2SO2 + O2 = 2SO3

вгазовой фазе установилось состояние равновесия. Как изменится скорость прямой реакции, если объем газовой смеси уменьшить в три раза? В каком направлении сместится равновесие?

Решение.

Запишем выражение основного постулата химической кинетики для прямой реакции, полагая её простой:

vпр = k [SO2]2 [O2].

После уменьшения объема смеси в три раза концентрация каждого из реагирующих веществ увеличится в три раза. При новых концентрациях скорость реакции изменится:

vx = k (3[SO2])2 3[O2].

Отсюда vx/vпр=32 .3=27, следовательно, скорость прямой реакции увеличится в 27 раз.

Если объем газовой смеси уменьшить в три раза, то по закону Бойля-Мариотта давление возрастет втрое. При увеличении давления равновесие, в соответствии с принципом Ле Шателье,

30

сместится в направлении веществ, занимающих меньший объем при нормальных условиях. В данном случае 2 моля SO2 и 1 моль O2 в сумме занимают объем больший, чем 2 моля SO3 (закон Авогадро). Следовательно, равновесие сместится вправо, в направлении образования SO3.

2. Как изменится скорость реакции при повышении температуры от 30 до 70°С, если температурный коэффициент скорости этой реакции равен 2.

Решение.

Поскольку нам дан температурный коэффициент скорости реакции γ=2, то мы можем использовать правило Вант-Гоффа:

70−30

v(70) = v(30) 2 10 = v(30) 24 = 16v(30) ,

Следовательно, при повышении температуры от 30 до 70°С скорость реакции увеличится в 16 раз.

3. Реакция разложения пентахлорида фосфора протекает по уравнению:

PCl5 (г) = PCl3 (г) + Cl2 (г) ; ∆H = 92,59кДж

Как надо изменить: а) температуру, б) давление, чтобы сместить равновесие в направлении реакции разложения РС15? Как изменится положение равновесия, если добавить ещё хлора?

Решение.

Используем принцип Ле Шателье.

а) Так как реакция разложения РС15 – эндотермическая (∆H>0), то для смещения равновесия в направлении прямой реакции нужно повысить температуру.

б) Так как в прямой реакции разложение РС15 ведет к увеличению объема (из одного моля газа образуются два моля газов), то для смещения равновесия в направлении прямой реакции надо уменьшить давление.

Если повысить концентрацию Cl2, то равновесие сместится в направлении его расходования, т.е. – в сторону образования

PCl5.

31

2.4. Лабораторная работа №2. Изучение скорости разложения пероксида водорода газометрическим методом

Цель работы. Ознакомиться с газометрическим методом измерений, получить кинетические кривые, определить порядок и константу скорости реакции.

Пероксид водорода в водных растворах разлагается по стехиометрическому уравнению

2H2O2 = 2H2O + O2 .

В присутствии катализатора (например, дихромата калия K2Cr2O7) разложение перекиси водорода значительно ускоряется. Будучи каталитической, эта реакция не является простой и протекает в несколько стадий, важнейшими из которых являются последовательные стадии образования промежуточного продукта K2Cr2O8 и его реакции с молекулой пероксида с образованием кислорода:

K2Cr2O7 + H2O2 = K2Cr2O8 + H2O,

K2Cr2O8 + H2O2 = K2Cr2O7 + H2O + O2 .

По прошествии с момента начала реакции определенного времени устанавливается стационарная, незначительно изменяющаяся концентрация промежуточного продукта. С этого момента кинетика процесса соответствует первому порядку по кислороду.

Объем выделившегося кислорода Vt легко измерить, ис-

пользуя газометрический метод (см. рис. 1). Метод основан на вытеснении выделяющимся в процессе химической реакции в реакционном сосуде 1 газом жидкости из калиброванной стеклянной трубки (бюретки 2). Поскольку измерения объема выделившегося газа должны приводиться к атмосферному давлению,

уровень жидкости в бюретке должен совпадать с уровнем в сообщающемся с ней уравнительном сосуде 3 в течение всего

эксперимента!

Однако, кислород является продуктом реакции, а не реагентом. Для того, чтобы получить кинетические зависимости для исходного вещества, в данной работе используется величина,

32

пропорциональная его концентрации: V∞ − Vt . Здесь V∞ - объем

выделившегося кислорода при условии полного разложения пероксида водорода. Эта величина представляет собой количество кислорода, на данный момент еще не выделившегося, а это количество – пропорционально концентрации еще не разложившегося реагента.

Порядок выполнения работы.

Подготовить в лабораторном журнале таблицу для занесения в нее экспериментальных данных по форме табл. 3, принимая во внимание, что число отсчетов в ходе эксперимента может доходить до 30.

Таблица 3. Данные кинетического эксперимента, полученные

газометрическим методом

1.Отмерить цилиндром (шприцем) 2 мл 3%-ного раствора пероксида водорода и через коническую воронку осторожно влить в реакционную колбу 1 (см. рис. 2).

2.Открыть кран 5 делительной воронки, кран 6 бюретки, и с помощью уравнительного сосуда установить уровень жидкости в бюретке 2 на нулевое деление. Закрыть краны 5 и 6. В делительную воронку 4 залить 1 мл 0,05 М раствора дихромата калия.

3.Слить раствор дихромата калия в реакционную колбу, открыв кран 5. Реакционная смесь темнеет за счет образования промежуточного продукта. Закрыть кран 5, открыть кран 6 и сравнять уровни жидкости в бюретке и уравнительном сосуде. Снять первый отсчет, соответствующий t=0 и Vt=0, и занести его

втаблицу. Отсчет объема выделившегося кислорода по бюретке производить каждую минуту, постоянно следя за равенством уровней жидкости в бюретке и уравнительном сосуде 3.