§6. Непрерывность функции в точке х0

Пусть функция f(x) определена в некоторой окрестности точки x₀

Определение 6.1

Функция f(x) называется непрерывной в точке х₀, если она определена в точке х₀ и в некоторой ее окрестности существует предел функции при хх₀ и он равен значению функции в этой точке, т.е.

Определение 6.2

Функция f(x) называется непрерывной в точке х₁, х₂, … , х_n, … аргумента х₀, соответствующая последовательность f(х₁), f(х₂), … , f(х_n), … значений функции f(х₀).

Определение 6.3

f(x) – непрерывная в точке х₀ для любого𝜉>0 существует >0 для любых х

|x-x₀|<=> |f(x)-f(x₀)|< 𝜉

Определение 6.4

С учетом того, что , аназывается приращением аргумента в точке:,

- приращение функции в точке

, то

f(x) называется непрерывной в точке , если ее приращение в этой точке стремится 0 при стремлении к 0 приращения аргумента в этой точке, т.е.

Таким образом, приращение функции в точке является б.м. при.

Теорема 6.1 (арифметические действия над непрерывными функциями)

Пусть f(x) и g(x) – непрерывные функции в точке f(x)+g(x), f(x)(g(x)– непрерывны в этой точке.

2. Непрерывность некоторых элементарных функций

Одно из важнейших свойств элементарных функций – их непрерывность в любой точке, в окрестности которой они определены.

Непрерывность рациональных функций

Простейший пример функции, непрерывной в точке является постоянная функция, т.к.Кроме того,

Дробно-рациональная: R(x)=,n

Непрерывны в любых точках х, в которых ее знаменатель не равен 0 как частное непрерывных функций.

Непрерывность тригонометрических функций

Показать, что функция sin x непрерывна в любой точке х.

Непрерывность cos x в любой точке х будет доказываться аналогично.

Непрерывность функции sin x и cos x по теореме 6.1 => непрерывность функций tgx = иsec x = для любого х {x=} и функцийctg x = иcosec x = 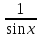для любого х {x=}

Непрерывность функции f(x)=|x|

f(x)=|x|=

Эта функция определена непрерывна во всех точках числовой прямой. В точках полупрямой (0;) она непрерывна, т.к. при х>0f(x)=x;

В точках полупрямой (- ; 0) она непрерывна, т.к. приx>0, f(x)= - х и ее можно представить как произведение 2-х непрерывных функций (-1) и х и применить теорему 6.1 о непрерывности произведения

Чтобы установить непрерывность функции |x| в точке х=0, вычислим односторонние пределы функции в этой точке:

=

=

Таким образом, пределы функции в точке х=0 слева и справа совпадают и равны значению функции в этой точке => функция |х| непрерывна в точке х=0 => непрерывна в любом х числовой прямой. Таким образом, рассмотренные функции непрерывны в любой точке, в окрестности которой они определены. На основании теоремы 5.1 о непрерывности Р, П и Ч мы утверждаем, что функции, получаемые из них с помощью конечного числа арифметических действий, является также непрерывными функциями в любой точке, в окрестности которой они определены.

Функция f(x) непрерывна в интервале (a,b), если она непрерывна в любой точке этого интервала; непрерывна на отрезке [a,b], если она непрерывна в интервале (a,b), непрерывна справа в точке а и слева в точке b, т.е.

Теорема 6.2 (непрерывность сложной функции)

Пусть функция z=(x) непрерывна в точке х₀, а функция у=f(z) непрерывна в точке z₀=(х₀), тогда сложная функция y=f((x)) непрерывна в точке х₀

Функция непрерывна на множестве Х, если она непрерывна в любой точке этого множества.