Типовой расчет по дискретной математике множества. Комбинаторика. Графы и сети вариант 4

1. Упростить, используя булевы тождества:

(после упрощения в формуле должно быть не менее трех букв).

2. Представить множество в виде суммы конституент:

.

3. Справедливо ли следующее теоретико-множественное тождество:

4. Какое из отношений

1) ; 2); 3): 4) никакое из указанных в 1)-3)

имеет место для множеств и :

, ?

5. Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 2 экземпляра другой и 1 экземпляр третьей книги. Сколькими способами могут быть вручены премии, если в олимпиаде участвовало 20 человек и никому не дают двух книг сразу?

6. Сколькими способами можно переставить буквы слова «опоссум» так, чтобы буква «п» шла непосредственно после буквы «о»?

7. Рота состоит из 3 офицеров, 6 сержантов и 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из одного офицера, двух сержантов и 20 рядовых?

8. В отделе НИИ работают несколько человек, причем каждый из них знает хотя бы один иностранный язык. Шестеро знают английский, шестеро – немецкий, семеро – французский. Четверо знают английский и немецкий, трое – немецкий и французский, двое – французский и английский. Один человек знает все три языка. Сколько человек работает в отделе? Сколько из них знают только английский язык? Только французский?

9. Найти производящую функцию последовательности

,

где .

10. Найти решение линейного рекуррентного соотношения

; ,.

11. Выделить компоненты связности графа, заданного матрицей смежности . Определить степени вершин и цикломатическое число графа.

.

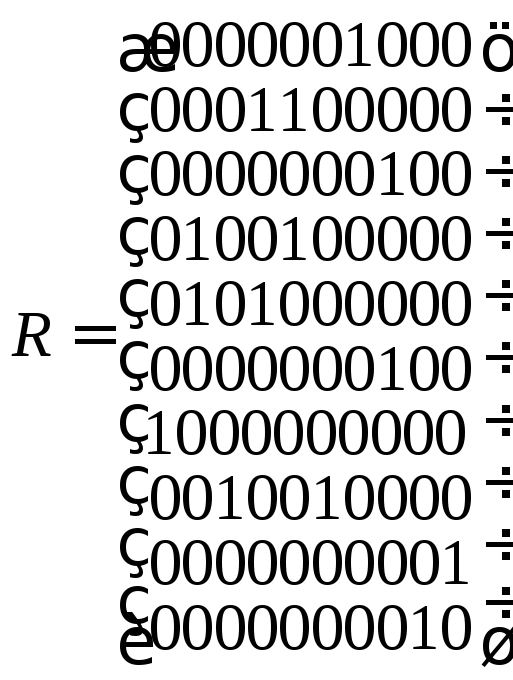12. Найти диаметр, радиус и центры графа:

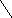
13. Построить кратчайшую цепь между вершинами ив ненагруженном графе:

14. Построить кратчайшую цепь между вершинами и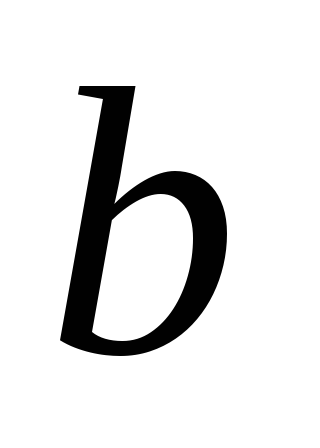в нагруженном графе:

10

1 10 1 2 5

_{10 4 2}

_{6 4 1 5 8}

_{3 5}

3 2 6 3

₈

15. Построить кратчайший остов для графа, заданного матрицей расстояний между его вершинами:

.

16. Для данного графа построить две системы базисных циклов. Выразить циклы одной системы через циклы другой.

17. Построить максимальный поток в транспортной сети:

_{10 12}

2 2 2 6

_{1 4 6}

_{6 2 4 4}

_{14 10}

18. Определить словарный ранг матрицы:

.

19. В сетевом графике найти критический путь, ранние и поздние сроки свершения событий, резервы времени и коэффициенты напряженности работ:

_{5 3}

_{7 7 2}

_{5 10 4 9 7}

3 1 5 _{12 15 конец}

2 5 5

_{5 2 9 5}

начало 7 11 5 1 ₅

_{3 11 5}

20. Построить сетевой график по заданной упорядоченности работ и определить критическое время выполнения всей совокупности работ: