
- •Типовой расчет по дискретной математике множества. Комбинаторика. Графы и сети вариант 1
- •Типовой расчет по дискретной математике множества. Комбинаторика. Графы и сети вариант 2
- •Типовой расчет по дискретной математике множества. Комбинаторика. Графы и сети вариант 3
- •Типовой расчет по дискретной математике множества. Комбинаторика. Графы и сети вариант 4
- •Типовой расчет по дискретной математике множества. Комбинаторика. Графы и сети вариант 5
Типовой расчет по дискретной математике множества. Комбинаторика. Графы и сети вариант 3
Упростить, используя булевы тождества:
![]()
(после упрощения в формуле должно быть не менее трех букв).
Представить множество в виде суммы конституент:
![]() .
.
Справедливо ли следующее теоретико-множественное тождество:
![]()
Какое из отношений
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() :
4) никакое из указанных в 1)-3)
:
4) никакое из указанных в 1)-3)
имеет
место для множеств
![]() и
и
![]() :
:
![]() ,
,
![]() ?
?
Найти число целых положительных чисел, не превосходящих 1000 и не делящихся ни на одно из чисел 6, 10 и 15?
Сколько имеется шестизначных чисел, у которых три цифры четные, а три нечетные (допускаются шестизначные числа, начинающиеся с нуля)?
Сколько различных браслетов можно сделать из пяти одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?
В комнате студенческого общежития живут трое студентов. У них есть 4 чашки, 5 блюдец и 6 чайных ложек (все чашки, блюдца и ложки отличаются друг от друга). Сколькими способами они могут накрыть стол для чаепития (каждый получает одну чашку, одно блюдце и одну ложку).
Найти
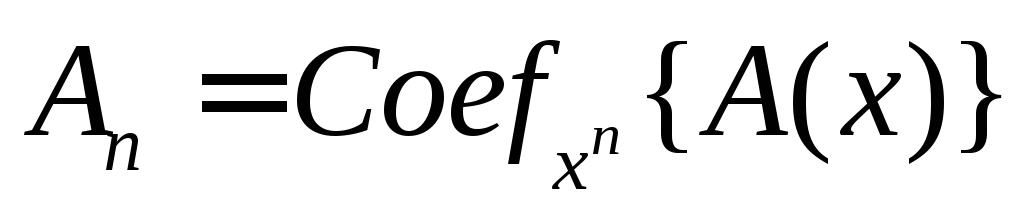 ,
где
,
где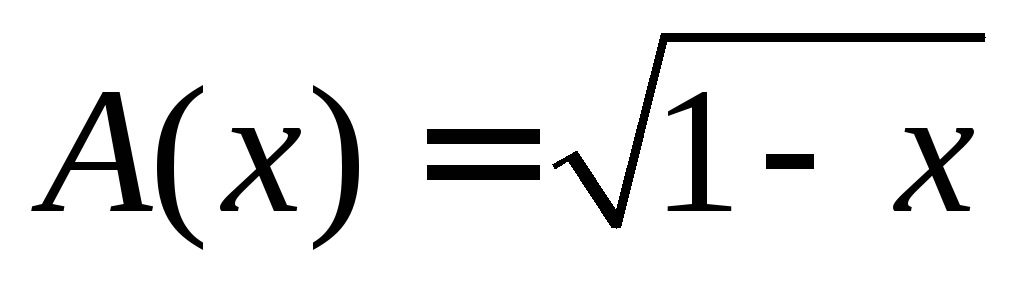 .
.
Найти решение линейного рекуррентного соотношения
![]() ;
;
![]() ,
,![]() .
.
Выделить компоненты связности графа, заданного матрицей смежности
 .
Определить степени вершин и цикломатическое
число графа.
.
Определить степени вершин и цикломатическое
число графа.
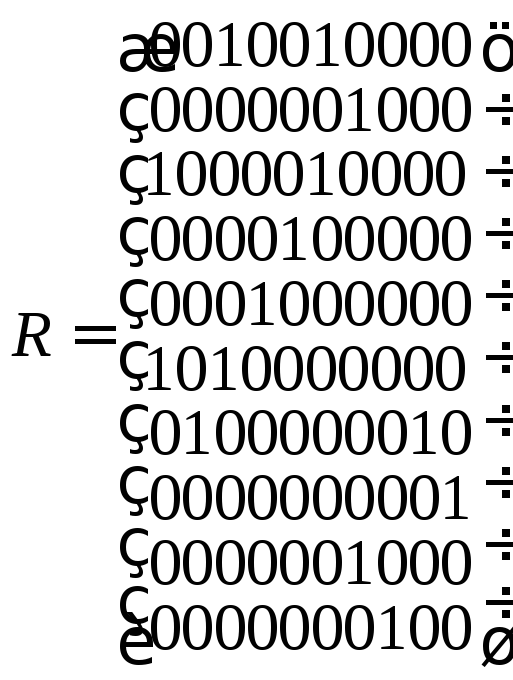 .
.
Найти диаметр, радиус и центры графа:





![]()
![]()
![]()






![]()
![]()
![]()
![]()

![]()
![]()
Построить кратчайшую цепь между вершинами
 и
и в ненагруженном графе:
в ненагруженном графе:








![]()
![]()
![]()
![]()
![]()
![]()








![]()
![]()
![]()
![]()
![]()







![]()
![]()
![]()
![]()
![]()




![]()
![]()
![]()
![]()
![]()
![]()
Построить кратчайшую цепь между вершинами
 и
и в нагруженном графе:
в нагруженном графе:







![]() 1
1
![]()
7
2 2 3 5 2









![]()
![]() 5
5
![]() 1
1
![]() 6
6
![]()
![]()
1
1 2 5 4 8

![]() 2
2
![]()
Построить кратчайший остов для графа, заданного матрицей расстояний между его вершинами:
 .
.
Для данного графа построить две системы базисных циклов. Выразить циклы одной системы через циклы другой.


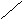
![]()





![]()
![]()
![]()
![]()
Построить максимальный поток в транспортной сети:

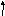
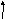

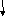

![]()
![]() 15
15
![]() 12
12
![]() 4
4
7 3 7




![]() 4
4
![]() 4
4
![]() 2
2
![]()
6 6 3 8


![]() 12
12
![]() 15
15
![]()
![]()
Определить словарный ранг матрицы:
 .
.
В сетевом графике найти критический путь, ранние и поздние сроки свершения событий, резервы времени и коэффициенты напряженности работ:





![]() 7
7
![]() 3
3
![]()
6 8 16
![]()







 5
5
![]() 6
12
6
12
![]() 16
4
16
4
![]() 8
8
6



 4
5
4
5
![]() 12
12
![]() 15
15
![]()
2 4 6 7
![]()










 7
7
![]() 2
2
![]() 4
4
![]() 7
7
![]() 5
5
![]() 5
5
![]()
![]()
начало 4 10 9 3 4 конец




![]() 8
8
![]() 7
7
![]() 4
4
![]() 6
6
![]()
Построить сетевой график по заданной упорядоченности работ и определить критическое время выполнения всей совокупности работ:
|
Работа |
|
|
|
|
|
|
|
|
|
|
Предшественники |
– |
– |
|
|
|
|
|
|
|
|
Продолжительность |
3 |
4 |
3 |
6 |
2 |
5 |
4 |
2 |
2 |
