
Karmazin_-_Teoria_Igr_Uchebnik / P4_3
.DOCТема 4. АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ В ЛИНЕЙНОМ
ПРОГРАММИРОВАНИИ
Рассмотрим каноническую задачу линейного программирования (1) (3) из темы 2:
![]()
![]() ,
,
![]() , (1)
, (1)
![]() ,
,
которую в дальнейшем будем называть прямой задачей.
Двойственной к задаче (1) называется задача
![]() , (2)
, (2)
![]() (3)
(3)
где
![]()
те же самые числа, что и в прямой задаче.
те же самые числа, что и в прямой задаче.
Для произвольной задачи линейного программирования двойственная к ней строится следующим образом. Исходная задача приводится к канонической, для которой затем строится двойственная. Полученная задача принимается в качестве двойственной к исходной задаче.
Теорема 1. Задачи (1) и (2), (3) взаимно двойственные.
Между свойствами взаимно двойственных задач линейного программирования имеется тесная связь.
Теорема 2.
Значение целевой функции прямой задачи
при любом её допустимом решении
![]() не превышает значения целевой функции
двойственной к ней задачи при любом её
допустимом решении
не превышает значения целевой функции
двойственной к ней задачи при любом её
допустимом решении
![]() ,
т.е.
,
т.е.
![]() .
.
Если для каких-нибудь
![]() и
и
![]() значения целевых функций совпадают,
т.е.
значения целевых функций совпадают,
т.е.
![]() ,
,
то
![]()
оптимальное решение прямой,
а
оптимальное решение прямой,
а
![]()
оптимальное решение двойственной
задачи.
оптимальное решение двойственной
задачи.
Теорема 3.
Пусть
![]() и
и
![]() допустимые
решения прямой и двойственной задач.
Для того чтобы они являлись оптимальными
решениями, необходимо и достаточно,
чтобы выполнялись условия дополняющей
нежесткости, а именно:
допустимые
решения прямой и двойственной задач.
Для того чтобы они являлись оптимальными
решениями, необходимо и достаточно,
чтобы выполнялись условия дополняющей
нежесткости, а именно:
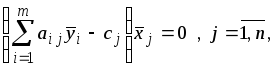
т.е. если
![]() ,
то
,
то
![]() ,
,
и если
![]() ,
то
,
то
![]() .
.
Теорема 4. Взаимно двойственные задачи разрешимы или неразрешимы одновременно, причем их оптимумы совпадают.
Если целевая функция одной из взаимно двойственных задач не ограничена сверху (соответственно, снизу) на своем допустимом множестве, то другая задача не имеет допустимых решений.
Теорема 5.
Пусть
![]()
некоторое оптимальное опорное решение
задачи (),
причем
некоторое оптимальное опорное решение
задачи (),
причем
![]()
его базис. Тогда вектор
его базис. Тогда вектор
![]() ,
удовлетворяющий системе линейных
алгебраических уравнений:
,
удовлетворяющий системе линейных
алгебраических уравнений:
![]() (4)
(4)
является оптимальным решением двойственной задачи (2) (3) .
Теорема 6. Если среди опорных оптимальных решений задачи (1) хотя бы одно обладает свойством невырожденности, то двойственная к ней задача имеет единственное оптимальное решение.
Обозначим через
![]() оптимум задачи (1),
где
оптимум задачи (1),
где
![]() .
Таким образом,
мы рассматриваем оптимум задачи (1),
а значит,
и задачи (2)
(3), как функцию параметров задачи.
.
Таким образом,
мы рассматриваем оптимум задачи (1),
а значит,
и задачи (2)
(3), как функцию параметров задачи.
Теорема 7.
Если оптимальные множества пары взаимно
двойственных задач ограничены, то
оптимум
![]() есть непрерывная, в точке
есть непрерывная, в точке
![]() ,
функция параметров этих задач.
,
функция параметров этих задач.
Теорема 8.
Если прямая задача (1)
имеет единственное оптимальное опорное
решение
![]() ,
то в точке
,
то в точке
![]() существуют частные производные
существуют частные производные
![]() ,
причем
,
причем
![]() . (5)
. (5)
Теорема 9. Если
двойственная задача (2), (3) имеет
единственное оптимальное решение
![]() ,
то в точке
,
то в точке
![]() существуют частные производные
существуют частные производные
![]() ,
причем
,
причем
![]() . (6)
. (6)
Теорема 10. Если
взаимно двойственные задачи (1)
и (2), (3) имеют единственные оптимальные
решения
![]() и
и
![]() соответственно,
то в точке
соответственно,
то в точке
![]() существуют частные производные
существуют частные производные
![]() ,
причем
,
причем
![]() . (7)
. (7)
В условиях
существования соответствующих частных
производных оптимума и
![]() определим так называемые коэффициенты
эластичности:
определим так называемые коэффициенты
эластичности:
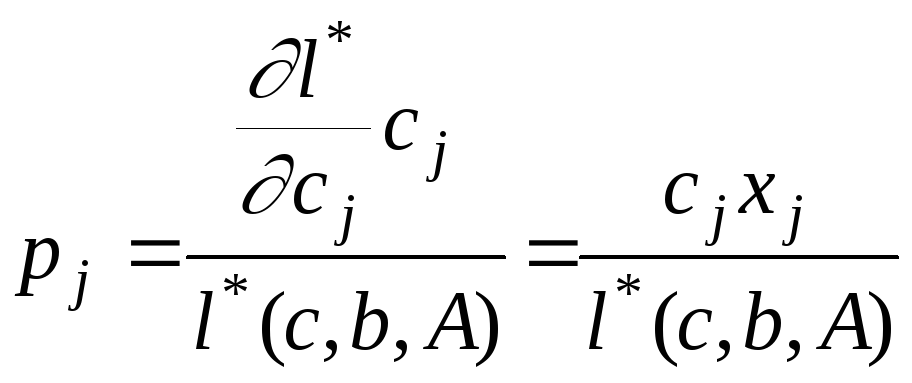 , (7)
, (7)
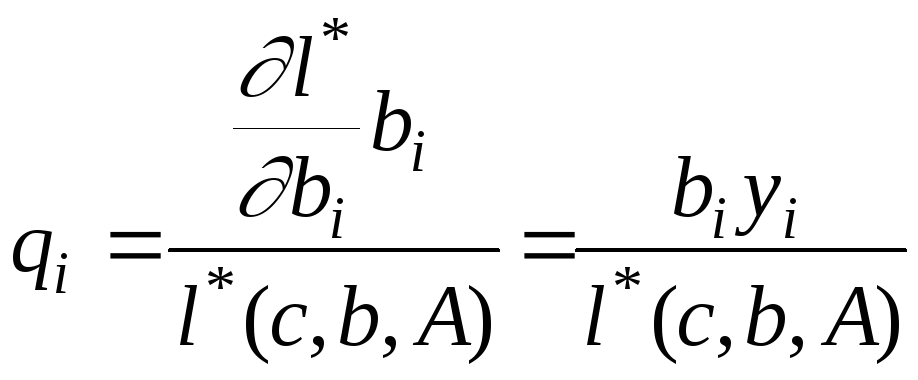 , (8)
, (8)
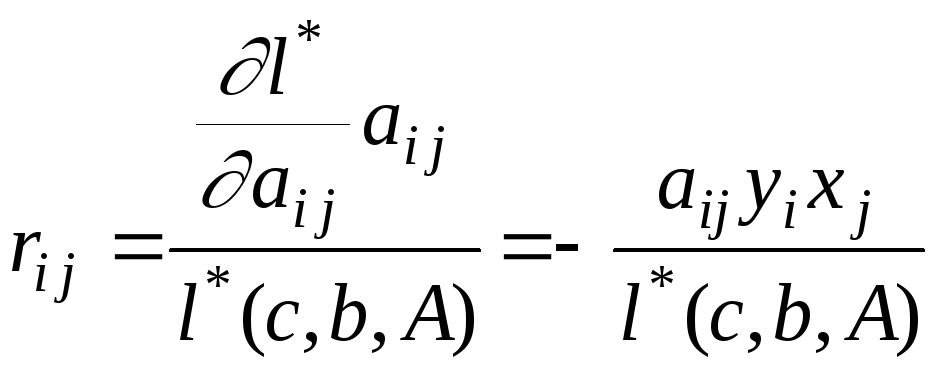 . (9)
. (9)
По величине
коэффициента эластичности можно судить
о чувствительности оптимума к малым
изменениям соответствующего параметра
задачи линейного программирования. А
именно: если
![]()
некоторый коэффициент эластичности,
то при
некоторый коэффициент эластичности,
то при
![]() оптимум устойчив,
при
оптимум устойчив,
при
![]()
нейтрален и при
нейтрален и при
![]()
неустойчив к малым изменениям
соответствующего параметра задачи.
неустойчив к малым изменениям
соответствующего параметра задачи.
Пример 1. Провести анализ чувствительности для задачи линейного программирования из примера 1 темы 3.
Как было показано,
оптимальным опорным решением указанной
задачи является вектор
![]() =(1,0,3,0,3),
имеющий следующие базисные вектора:
=(1,0,3,0,3),
имеющий следующие базисные вектора:
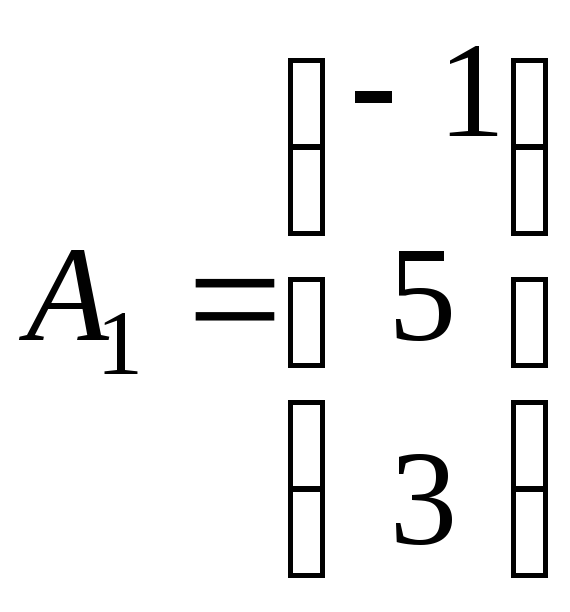 ,
,
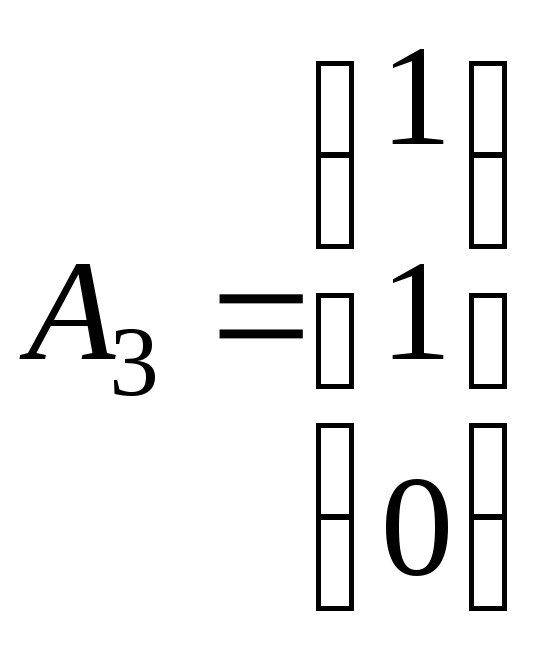 ,
,
 .
.
Таким образом,
![]()
Так как
![]() является невырожденным опорным решением,
то двойственная задача имеет единственное
решение
является невырожденным опорным решением,
то двойственная задача имеет единственное
решение
![]() .
Найдем его.
.
Найдем его.
Для этого составим систему вида (3):
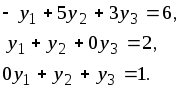
Решив эту систему,
находим, что
![]() =(1/3,
5/3, -2/3). При этом заметим,
что
=(1/3,
5/3, -2/3). При этом заметим,
что
![]() ,
,
т.е. решение двойственной задачи найдено верно.
В условиях нашего примера существуют частные производные оптимума по всем параметрам исходной задачи линейного программирования. По формулам (7) (9) вычисляем коэффициенты эластичности:
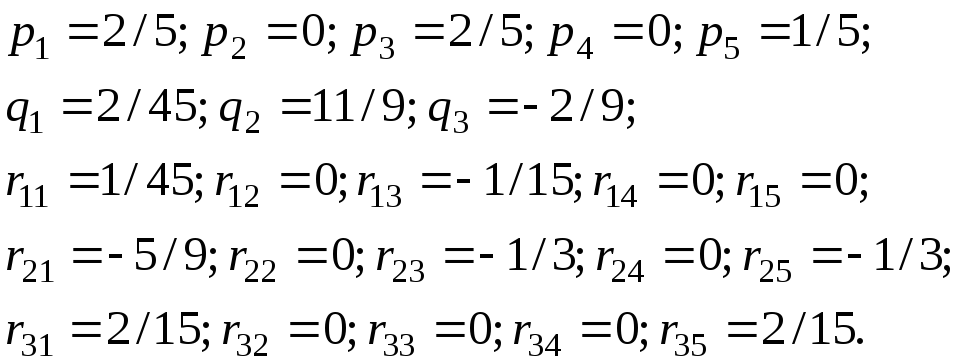
Таким образом,
решение рассматриваемой задачи линейного
программирования устойчиво к малым
изменениям всех параметров, кроме
![]() ,
т.к.
,
т.к.
![]() .
.
Задание. Провести анализ устойчивости канонической задачи линейного программирования из 3.1 3.102.
