Karmazin_-_Teoria_Igr_Uchebnik / P2_3

Тема 2. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ СИМПЛЕКС-МЕТОДОМ

В данном разделе речь пойдет об основном методе решения задач линейного программирования  симплекс-методе (методе последовательного улучшения плана). Для решения этим методом задачу надо привести к каноническому виду.

Канонической задачей линейного программирования будем называть следующую задачу:

(1)

, , (2)

, (3)

где  заданные вещественные числа, причем ;  искомые неизвестные. Предполагается, что .

Любую задачу линейного программирования можно привести к каноническому виду.

Функция , подлежащая максимизации, называется целевой функцией. Условия (2.2) и (2.3) называются ограничениями задачи.

Любой вектор , удовлетворяющий всем ограничениям (2.2), (2.3) , называется допустимым решением задачи, а совокупность всех допустимых решений  допустимым множеством. Допустимое решение задачи называется ее оптимальным решением или решением , если

,

где D  допустимое множество задачи. Множество всех оптимальных решений называется оптимальным. Величина называется оптимальным значением целевой функции или оптимумом.

Теорема 1. Допустимое и оптимальное множества задачи (1)  (3) замкнуты и выпуклы, если не пусты.

Для формулировки метода решения задачи (1)  (3) запишем ее в следующем виде:

,

,

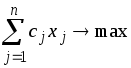³ 0, ,

где .

Допустимое решение называется опорным решением (опорным планом) задачи (1)  (3), если векторы , соответствующие компонентам , в совокупности линейно независимы.

Опорное решение будем называть невырожденным, если оно имеет положительных компонент, и вырожденным в противном случае.

Любую совокупность  мерных линейно независимых векторов, содержащую в качестве подсистемы все вектора , соответствующие положительным компонентам опорного решения , будем называть базисом опорного решения . Положительные компоненты опорного решения будем также называть базисными. Ясно, что базис невырожденного опорного решения определен однозначно.

Теорема 2. Для того чтобы точка являлась вершиной допустимого множества задачи (1)  (3), необходимо и достаточно, чтобы вектор являлся опорным решением этой задачи.

Задача (1)  (3) всегда имеет опорные решения, если её допустимое множество не пусто.

Соседним вершинам допустимого многогранника D (т.е. лежащим на одном и том же ребре) соответствуют опорные решения, базисы которых отличаются лишь одним вектором.

Пусть  опорное решение задачи (1)  (3) с базисом

. (4)

Обозначим через - ю координату вектора , в базисе (4). Ясно, что , ; , , , , .

В общем случае вектор является решением следующей системы линейных алгебраических уравнений:

. (5)

Для каждого вектора ( ) определим величину

, (6)

которую будем называть оценкой для A_j в базисе (4). Ясно, что .

Теорема 3 (критерий оптимальности опорного плана). Опорное решение тогда и только тогда является оптимальным решением задачи, когда все оценки .

Теорема 4 (признак неограниченности целевой функции задачи). Если для какого-нибудь опорного решения существует хотя бы одна оценка такая, что для неё все , то это означает, что целевая функция данной задачи линейного программирования, не ограничена сверху на допустимом множестве.

Пусть теперь для некоторого номера , система векторов

(7)

также является базисом в .

Обозначим через  -ю координату вектора в базисе (7). Тогда имеют место основные симплекс-формулы:

(8)

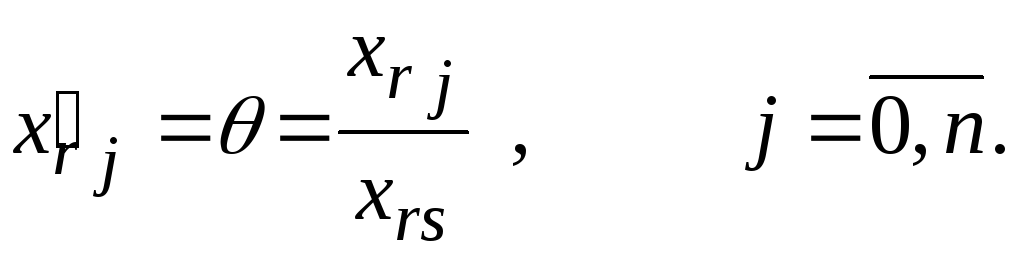
Теорема 5 (о возможности улучшения опорного решения). Если для данного опорного решения есть такая отрицательная оценка , что среди координат вектора в данном базисе (т.е. среди чисел ) есть положительные, то базис, которому соответствует лучшее опорное решение, получим, заменив вектором тот вектор исходного базиса, для которого , причем для всех .

Теорема 6 (критерий единственности оптимального опорного решения). Если для данного опорного решения все оценки , причем нулевые оценки соответствуют только базисным векторам, то данное опорное решение является единственным оптимальным опорным решением задачи.

Алгоритм симплекс-метода

Пусть известно какое-нибудь опорное решение задачи (1)  (3) с базисом (4).

1. Полагаем 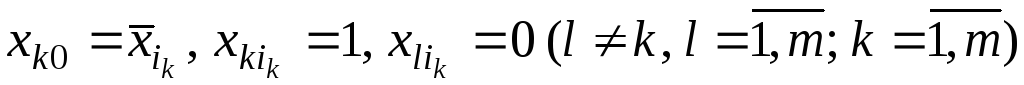. Для находим 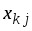, решая систему (5).

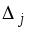2. Для каждого вычисляем оценку по формуле (6), причем 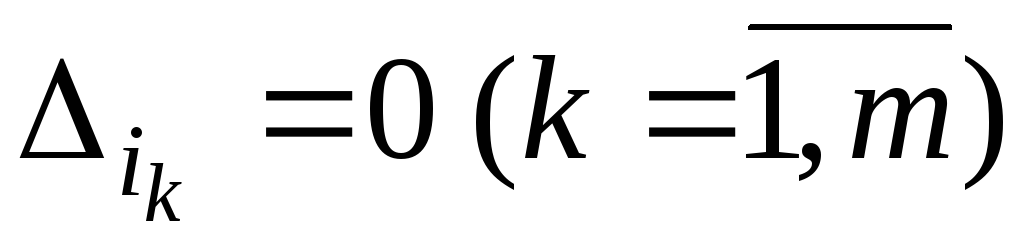. Если все , то процесс решения задачи окончен. Рассматриваемое опорное решение оптимально. Оптимум целевой функции

. (9)

Если есть , то:

3. Выясняем, существует ли хотя бы одна такая , что все .

Если существует, то процесс решения задачи окончен  целевая функция не ограничена сверху на допустимом множестве.

Если таких нет (т.е. для любой есть хотя бы одно ), то:

4. Выбираем одну из (например, для); вычисляем отношения для всех k, для которых 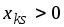, и найдем минимальное из этих отношений (пусть это будет ).

5. Осуществляем переход к новому опорному решению (базис которого получается заменой вектора в предыдущем базисе вектором ), вычислив координаты 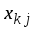векторов 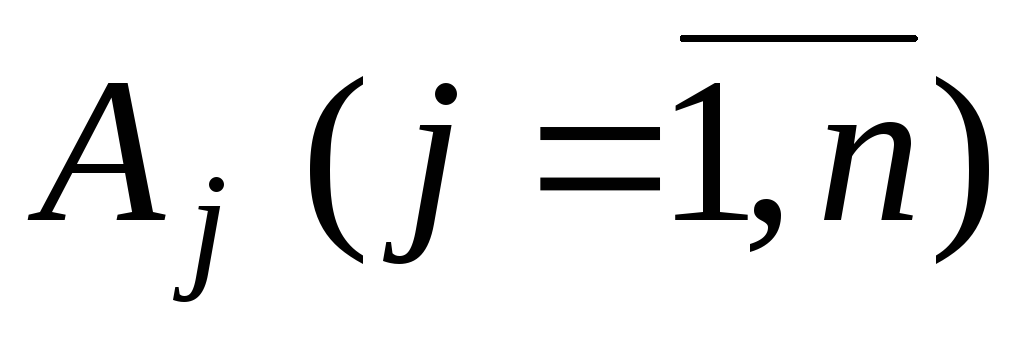в новом базисе по основным симплекс-формулам (8).

Переходим к шагу 2.

Каждый переход к новому базису называется итерацией симплекс-метода. В невырожденном случае через конечное число итераций процесс закончится либо на п.2 , либо на п.3. В вырожденном случае возможно зацикливание, но оно маловероятно.

Пример 1. Решить симплекс-методом задачу линейного программирования

Сначала приведем задачу к каноническому виду, для этого в каждое ограничение введем неотрицательные переменные , и заменим знаки неравенств на знаки равенств. В результате получим задачу линейного программирования, в канонической форме, эквивалентную исходной задаче.

(10)

.

О

порным решением канонической задачи является вектор , а базисом  единичные векторы . Решаем задачу симплекс-методом, результаты вычислений оформляем в виде симплекс-таблиц. В самой верхней строке таблицы, в клетках, расположенных над символами , записывают значения соответствующих коэффициентов целевой функции.

Таблица 1

	№	Базис	Сбаз	A0	6	7	0	0	0
					A1	A2	A3	A4	A5
	1	A3	0	3	3	-5	1	0	0
	2	A4	0	39	5	3	0	1	0
	3	A5	0	9	-5	"3"	0	0	1
	4	-	-	0	-6	-7	0	0	0

В колонке "Базис" перечислены наименования базисных векторов, эта последовательность векторов всегда должна образовывать единичную матрицу. В колонке "С_баз" для удобства вычислений приведены значения коэффициентов целевой функции при базисных переменных, в алгоритме они обозначены символами , где k  номер строки в таблице. В колонках табл. 1 содержатся коэффициенты системы ограничений-равенств (10). В алгоритме эти коэффициенты обозначены символами , где i номер строки в табл. 1, а индекс j соответствует индексу в столбце . В 4-й строке записываются значения и критериев , которые вычисляются по формулам (6).

Анализируя табл. 1 видим, что отрицательными оценками являются , причем является наименьшей из них: . Во всех столбцах с отрицательными присутствуют положительные элементы. Это означает, что данное опорное решение не оптимально и нет основания утверждать, что целевая функция задачи не ограничена сверху на допустимом множестве. Таким образом, вектор следует ввести в базис (этот факт отмечен стрелкой сверху). Затем ищем вектор, который следует вывести из базиса. Для этого находим отношения

Минимальное отношение =3. Следовательно, из базиса выводим третий (по занимаемому месту) вектор . Этот факт отмечен стрелкой слева. Ведущий элемент выделен жирным шрифтом и апострофами.

Заполняем симплекс-таблицу, соответствующую новому опорному решению. Для этого используем основные симплекс-формулы (8). При этом сначала заполняем 3-ю строку табл.2, полагая

Таблица 2

	№	Базис	Сбаз	A0	6	7	0	0	0
					A1	A2	A3	A4	A5
	1	A3	0	18	-16/3	0	1	0	5/3
	2	A4	0	30	"10"	0	0	1	-1
	3	A2	7	3	-5/3	1	0	0	1/3
	4	-	-	21	-53/3	0	0	0	7/3

Из табл. 2, видим, что отрицательной оценкой является , следовательно новый опорный план неоптимальный и его можно улучшить, если введем в базис вектор .

В столбце, соответствующем , только элемент второй строки положителен, следовательно выводим из базиса вектор . Выделяем ведущий элемент и заполняем следующую табл. 3.

Таблица 3

	№	Базис	Сбаз	A0	6	7	0	0	0
					A1	A2	A3	A4	A5
	1	A3	0	34	0	0	1	8/15	17/15
	2	A1	6	3	1	0	0	1/10	-1/10
	3	A2	7	8	0	1	0	1/6	1/6
	4	-	-	74	0	0	0	53/30	17/30

Сначала вычисляем элементы 2-й строки, затем элементы остальных строк. В новой симплекс таблице все неотрицательные, следовательно, получен оптимальный опорный план канонической задачи: , а  максимальное значение целевой функции.

Оптимальным опорным решением исходной задачи является вектор .

Задание. Задачу линейного программирования из 1.11.104 привести к каноническому виду и решить симплекс-методом.

21