Karmazin_-_Teoria_Igr_Uchebnik / P6_3

Тема 6. РЕШЕНИЕ ЗАДАЧ

ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

ДВОЙСТВЕННЫМ СИМПЛЕКС-МЕТОДОМ

Из теории двойственности вытекает ряд методов решения задач линейного программирования. Синтез симплекс-метода (метода последовательного улучшения плана) и основных идей двойственности приводит к двойственному симплекс-методу (методу последовательного улучшения оценок).

Рассмотрим пару взаимно двойственных задач, прямую каноническую задачу линейного программирования

(1)

, , (2)

(3)

и двойственную к ней:

, (4)

. (5)

Допустимое решение двойственной задачи (т.е. удовлетворяющее ограничениям (5)) будем называть опорным планом, если среди (5), которые обращает в равенства, имеется линейно независимых условий.

Базисом опорного плана назовем произвольную систему из линейно независимых векторов столбцов прямой задачи (1)  (3) , для которых

. (6)

Базис опорного плана двойственной задачи будем называть двойственным базисом.

Опорный план называется невырожденным, если для любого вектора , не входящего в его базис ,

.

С каждым опорным планом двойственной задачи (точнее с его базисом) удобно связывать некоторый -мерный вектор , удовлетворяющий условиям (2) прямой задачи. Такое соответствие позволит в дальнейшем формулировать в терминах прямой задачи все построения, относящиеся к опорным решениям двойственной задачи.

Разложим вектор ограничений задачи (1)  (3) по двойственному базису . Обозначим соответствующие коэффициенты разложения через ; -мерный вектор , -е компоненты которого совпадают с , а остальные равны нулю, будем называть псевдопланом прямой задачи. Компоненты назовем базисными, а остальные  внебазисными. Будем в дальнейшем пользоваться терминами "двойственный базис" и "базис псевдоплана" как синонимами.

Заметим, что некоторые из компонент псевдоплана могут быть отрицательными, так что он, вообще говоря, не является допустимым решением прямой задачи.

Псевдоплан можно определять и независимо от двойственной задачи. Пусть  произвольная система линейно независимых векторов условий (2). Обозначим систему индексов через _, разложим векторы условий и вектор ограничений по векторам :

, (7)

. (8)

Введем такое обозначение:

. (9)

Теорема 1. -мерный вектор , для которого , а при , является псевдопланом в том и только в том случае, если все .

Рассмотрим некоторое опорное решение двойственной задачи. Базис опорного решения состоит из векторов .

Ему соответствует псевдоплан с базисными компонентами .

Теорема 2 (критерий оптимальности псевдоплана). Если псевдоплан является допустимым решением задачи (1)  (3), то он является её оптимальным опорным решением.

Теорема 3 (об улучшении псевдоплана). Если для псевдоплана с положительными небазисными оценками есть такие, что среди есть , то получим новый псевдоплан с меньшим значением целевой функции, если выведем из базиса вектор и введем в базис вектор , для которых выполняются условия

и для всех и . (10)

Теорема 4. Если псевдоплан (но не допустимое опорное решение) задачи (1)  (3) таков, что среди есть хотя бы одно , и такое, что все , то данная задача линейного программирования не имеет допустимых решений.

Алгоритм двойственного симплекс-метода

Теоремы 2  4, вместе взятые, дают основание сформулировать алгоритм двойственного симплекс-метода. Пусть имеется псевдоплан задачи (1)  (3) и его базис.

1. Проверяем условие: 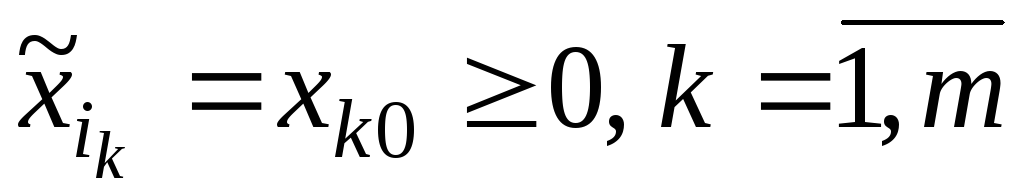. Если оно выполняется, то процесс решения задачи окончен: данный псевдоплан есть оптимальное опорное решение задачи (1)  (3).

Если среди есть отрицательные, то

2. Разлагаем все вектора 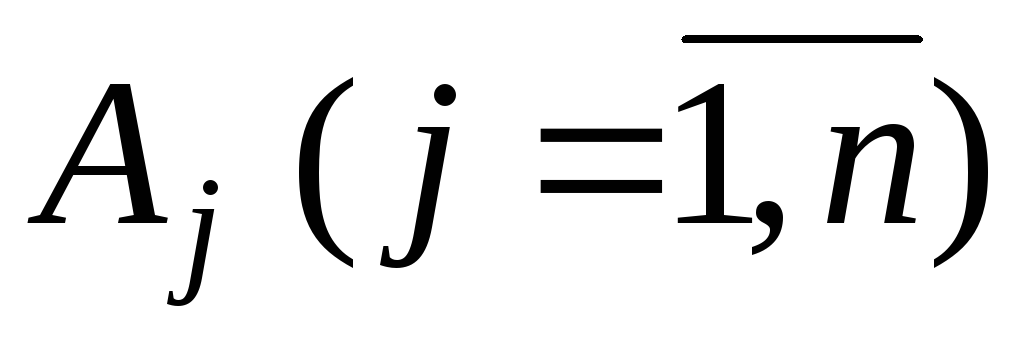по базису рассматриваемого псевдоплана (иными словами, находим все числа 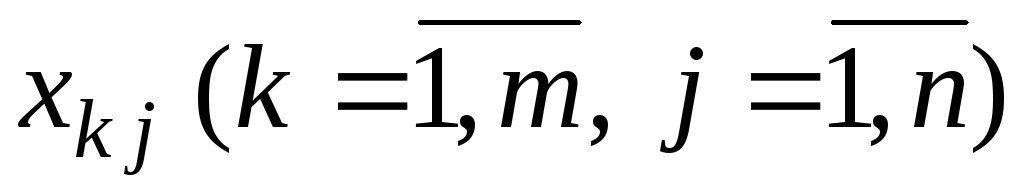) и просматриваем поочередно все 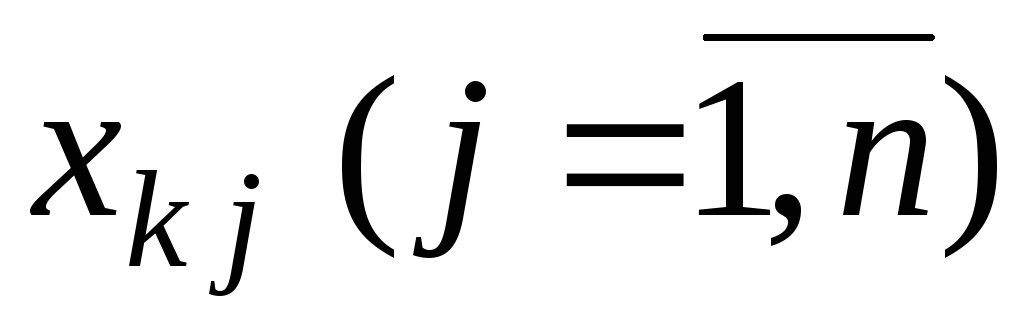для тех k, для которых .

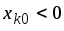Если есть такое , что для него все , то процесс окончен: задача не имеет допустимых решений.

Если таких нет, то

3. Выбираем одну из 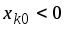(пусть это будет 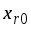) и для неё вычисляем отношения 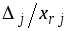для всех 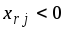. Из этих соотношений выбираем минимальное по абсолютной величине (пусть это будет 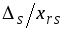). Переходим к новому псевдоплану, заменяя в базисе вектор 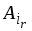вектором 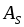. Переходим к п.1, имея ввиду новый псевдоплан. Координаты нового псевдоплана и, если потребуется, числа 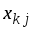находим по основным симплекс-формулам. Оценки 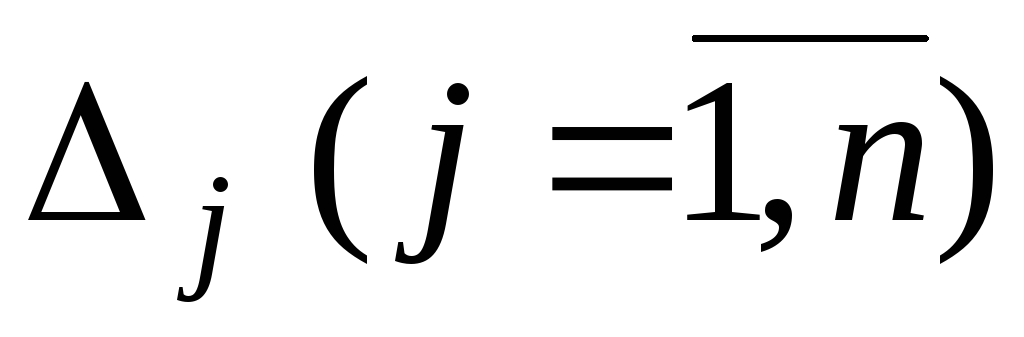для нового базиса находим по формуле (9) .

Каждый переход к новому базису будем называть итерацией двойственного симплекс-метода.

Пример 1. Решить двойственным симплекс-методом каноническую задачу линейного программирования, где

.

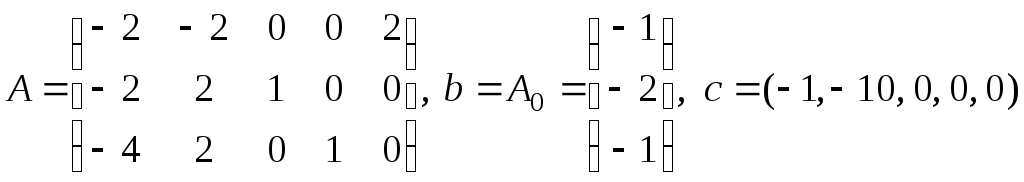Найдем исходный псевдоплан непосредственно из двойственной задачи:

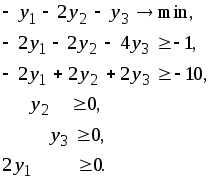
Вектор =(0, 0, 0) удовлетворяет всем ограничениям двойственной задачи и превращает три последние из них (с явно линейно независимыми векторами коэффициентов) в равенства. Следовательно, является опорным решением двойственной задачи с базисом . Тогда этот базис определяет псевдоплан прямой задачи. Найдем этот псевдоплан, разложив вектор по базису (а значит решаем систему вида ):

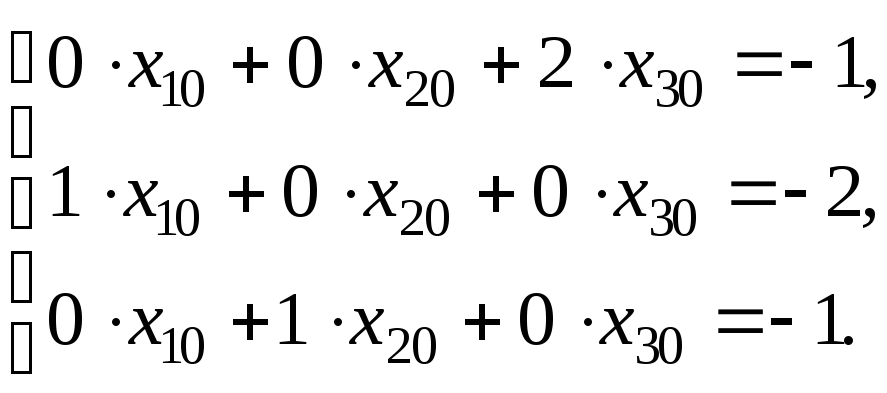
О

ткуда, . Следовательно,  псевдоплан прямой задачи. Так как не является допустимым, то оптимальное решение не найдено. Следуя двойственному симплекс-методу, заполняем исходную симплекс-таблицу.

Таблица 1

	№	Базис	Сбаз	A0	-1	-10	0	0	0
					A1	A2	A3	A4	A5
	1	A3	0	-2	"-2"	1	1	0	0
	2	A4	0	-1	-4	1	0	1	0
	3	A5	0	-1/2	-1	-1	0	0	1
	4	-	-	0	1	10	0	0	0

При этом числа определяются также как и , только в правой части решаемой системы находятся компоненты векторов соответственно.

Первые три строки соответствуют отрицательным координатам рассматриваемого псевдоплана. В каждой из них есть отрицательные . Следовательно, у нас нет основания сделать вывод о недопустимости задачи. Процесс необходимо продолжить.

Найдем вектор, который следует вывести из базиса. Выберем в качестве ведущей первую строку, соответствующую наименьшей отрицательной координате псевдоплана (). Чтобы определить вектор, который следует ввести в базис вместо вектора , найдем абсолютные величины отношений оценок к соответствующим им для всех отрицательных : . Получим . Следовательно, в нашем случае выбор ограничен одним вектором. Таким образом, в базис вводим вектор . Выводимый и вводимый векторы отмечены стрелками. Ведущий элемент (он выделен жирным шрифтом и отмечен кавычками) стоит на пересечении ведущей строки и столбца. Строим новую таблицу (так же, как и в обычном симплекс-методе). При этом учитываем, что целесообразно, прежде всего, найти базисные координаты нового псевдоплана, т.е. новые значения элементов столбца по основным симплекс-формулам. Получаем: . Так как все они неотрицательны, то согласно критерию оптимальности псевдоплана, имеем оптимальное решение задачи : .

Заполнять остальную часть таблицы нет необходимости, так как исходная задача решена.

Задание. Решить двойственным симплекс-методом каноническую задачу линейного программирования для значени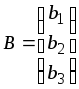й , и заданных в 6.1  6.108.

6.1 A=; B=.	6.2 A=; B=.
6.3 A=; B=.	6.4 A=; B=.
6.5 A=; B=.	6.6 A=; B=.
6.7 A=; B=.	6.8 A=; B=.
6.9 A=; B=.	6.10 A=; B=.
6.11 A=; B=.	6.12 A=; B=.
6.13 A=; B=.	6.14 A=; B=.
6.15 A=; B=.	6.16 A=; B=.
6.17 A=; B=.	6.18 A=; B=.
6.19 A=; B=.	6.20 A=; B=.
6.21 A=; B=.	6.22 A=; B=.
6.23 A=; B=.	6.24 A=; B=.
6.25 A=; B=.	6.26 A=; B=.
6.27 A=; B=.	6.28 A=; B=.
6.29 A=; B=.	6.30 A=; B=.
6.31 A=; B=.	6.32 A=; B=.

6.33 A=; B=.	6.34 A=; B=.
6.35 A=; B=.	6.36 A=; B=.
6.37 A=; B=.	6.38 A=; B=.
6.39 A=; B=.	6.40 A=; B=.
6.41 A=; B=.	6.42 A=; B=.
6.43 A=; B=.	6.44 A=; B=.
6.45 A=; B=.	6.46 A=; B=.
6.47 A=; B=.	6.48 A=; B=.

6.49 A=; B=.	6.50 A=; B=.
6.51 A=; B=.	6.52 A=; B=.
6.53 A=; B=.	6.54 A=; B=.
6.55 A=; B=.	6.56 A=; B=.
6.57 A=; B=.	6.58 A=; B=.
6.59 A=; B=.	6.60 A=; B=.
6.61 A=; B=.	6.62 A=; B=.
6.63 A=; B=.	6.64 A=; B=.

6.65 A=; B=.	6.66 A=; B=.
6.67 A=; B=.	6.68 A=; B=.
6.69 A=; B=.	6.70 A=; B=.
6.71 A=; B=.	6.72 A=; B=.
6.73 A=; B=.	6.74 A=; B=.
6.75 A=; B=.	6.76 A=; B=.
6.77 A=; B=.	6.78 A=; B=.
6.79 A=; B=.	6.80 A=; B=.

6.81 A=; B=.	6.82 A=; B=.
6.83 A=; B=.	6.84 A=; B=.
6.85 A=; B=.	6.86 A=; B=.
6.87 A=; B=.	6.88 A=; B=.
6.89 A=; B=.	6.90 A=; B=.
6.91 A=; B=.	6.92 A=; B=.
6.93 A=; B=.	6.94 A=; B=.
6.95 A=; B=.	6.96 A=; B=.

6.97 A=; B=.	6.98 A=; B=.
6.99 A=; B=.	6.100 A=; B=.
6.101 A=; B=.	6.102 A=; B=.
6.103 A=; B=.	6.104 A=; B=.
6.105 A=; B=.	6.106 A=; B=.
6.107 A=; B=.	6.108 A=; B=.

65