Karmazin_-_Teoria_Igr_Uchebnik / P9_3

Тема 9. РЕШЕНИЕ ЛИНЕЙНОЙ ЦЕЛОЧИСЛЕННОЙ ЗАДАЧИ

МЕТОДОМ ОТСЕЧЕНИЙ (МЕТОД ГОМОРИ)

Значительная часть экономических задач линейного программирования требует целочисленного решения. Задача целочисленного линейного программирования (ЦЛП) формулируется так же, как и задача линейного программирования, но включается дополнительное требование целочисленности решения.

, (1)

, (2)

, (3)

. (4)

Для краткости задачу (1)  (3) назовем задачей линейного программирования (ЛП), а задачу (1)  (4)  задачей ЦЛП. Предположим, что задача ЛП имеет решение и пусть  оптимальное решение задачи ЛП. Если полученный план целочисленный, то задача ЦЛП решена. В противном случае к ограничениям задачи ЛП добавляется новое линейное ограничение:

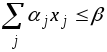, (5)

которое должно обладать следующими свойствами:

а) отсекать найденный оптимальный нецелочисленный план;

б) не отсекать ни одного целочисленного плана.

Ограничение (5), обладающее указанными свойствами, называется правильным отсечением.

Далее задача решается с учетом нового ограничения.

Рассмотрим достаточно простой способ построения правильного отсечения. Пусть  оптимальное решение задачи ЛП, и пусть обозначают элементы последней симплекс-таблицы, где соответствует номеру столбца , а  номеру строки в симплекс-таблице. Обозначим через множество индексов небазисных переменных. Согласно последней симплекс-таблице разложение столбца по столбцам можно записать в виде:

,

здесь  индекс базисной переменной, соответствующей строке .

Обозначим через ближайшее целое число, не превосходящее , и определим дробную часть числа : . (Например: ). Очевидно, что .

Пусть  нецелое. Рассмотрим равенство

. (6)

Оно должно выполняться для всех допустимых решений. Если небазисные переменные равны нулю, то из (6) следует, что  также нецелое. Из (6) следует, что для всех допустимых решений задачи ЛП должно выполняться неравенство

.

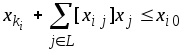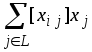
При любых целых сумма  целая величина и, следовательно, для всех целочисленных допустимых решений задачи ЦЛП должно выполняться неравенство

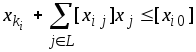. (7)

Представим равенство (6) в виде

,

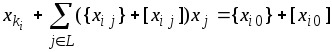вычитая его из неравенства (7), получим

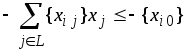. (8)

Теорема 1. Пусть ,  элементы последней симплекс-таблицы задачи ЛП, тогда неравенство (8) определяет правильное отсечение.

Алгоритм метода отсечений Гомори. Последовательность решаемых задач ЛП пометим индексом : .

1. Полагаем , соответствует исходная задача ЛП (1)  (3).

2. Симплексным методом решаем задачу без условия целочисленности. Если все компоненты оптимального плана целые, то он является оптимальным и для задачи ЦЛП. Если задача неразрешима (не имеет конечного максимума или условия противоречивы), то и задача ЦЛП также неразрешима.

3. Если среди компонент оптимального решения есть нецелые, то выбираем любую из них, можно при этом руководствоваться одним из следующих правил:

а) выбираем компоненту с наибольшей дробной частью;

б) выбираем среди дробных компонент компоненту с наибольшей целой частью;

в) выбираем компоненту с наименьшим номером .

Далее по соответствующему уравнению (6) формируем правильное отсечение (8).

4. Увеличиваем индекс: . Введением дополнительной целочисленной переменной преобразуем неравенство (8) в равносильное равенство

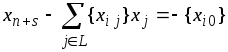, (9)

включаем его в систему ограничений и переходим к расширенной задаче . Переход к новой расширенной задаче ЛП осуществляется введением в симплекс-таблицу дополнительной строки и столбца и базисной переменной . В дополнительную строку с номером записываем: в столбец "Базис"  ; в столбец С_баз  0; в столбец  дробную часть со знаком минус; в столбцы базисных переменных  0; в столбцы небазисных переменных  дробные части со знаком минус; в столбец  "1". Во все остальные клетки столбца записываем 0. В результате мы пришли к псевдоплану расширенной задачи.

5. Новую расширенную задачу решаем двойственным симплекс-методом без условия целочисленности. Вектор не является опорным планом новой задачи , так как в нем присутствует отрицательная компонента с индексом . Согласно алгоритму двойственного симплексного метода выводим из базиса вектор , для определения вектора, вводимого в базис, строго следуем алгоритму двойственного симплексного метода. Если окажется, что среди элементов в столбцах , отсутствуют отрицательные элементы, то задача решения не имеет (условия задачи противоречивы), и, следовательно, задача ЦЛП (1)  (4) также не имеет решения. Для получения опорного плана расширенной задачи может понадобиться несколько шагов. Если все компоненты оптимального решения расширенной задачи целые, то отбросив дополнительные переменные из оптимального решения задачи, получаем оптимальное решение исходной задачи ЦЛП. Если среди компонент оптимального решения найдутся нецелые, то переходим к п. 3 нашего алгоритма.

Трудоемкость решения целочисленной задачи этим методом обусловлена вводом новых добавочных переменных и ограничений. Следующее правило, при большом числе шагов, позволяет ограничить число дополнительных переменных расширенной задачи до . Введенные на ранних шагах отсечения могут стать несущественными и без ущерба могут быть убраны из симплекс-таблицы. Число существенных отсечений не превосходит .

Правило исключения дополнительных переменных. Дополнительная переменная вводится как базисная переменная очередного псевдоплана и сразу, на этом же шаге, выводится из числа базисных переменных. Если на последующих шагах согласно правилу преобразования симплекс-таблицы дополнительная переменная снова окажется базисной, то ее значение станет несущественным для переменных исходной задачи, и, следовательно, строку и столбец текущей симплекс-таблицы можно вычеркнуть.

Пример 1. Решить методом отсечения Гомори следующую задачу ЦЛП:

;

и  целые.

Решаем задачу без условия целочисленности симплексным методом.

Таблица 1

	№	Базис	Сбаз	A0	2	8	2	0	0
					A1	A2	A3	A4	A5
	1	A3	2	16	6	-5	1	0	0
	2	A4	0	36	3	1	0	1	0
	3	A5	0	28	-6	"3"	0	0	1
	4	-	-	32	10	-18	0	0	0

Заполняем симплексную табл. 1. На первой итерации вводим в базис вектор A₂ и выводим из базиса вектор A₅. Ведущий элемент в симплекс-таблице выделен жирным шрифтом и апострофами. Выполнив необходимые преобразования для перехода в новый базис, получим табл. 2.

Таблица 2

	№	Базис	Сбаз	A0	2	8	2	0	0
					A1	A2	A3	A4	A5
	1	A3	2	188/3	-4	0	1	0	5/3
	2	A4	0	80/3	"5"	0	0	1	-1/3
	3	A2	8	28/3	-2	1	0	0	1/3
	4	-	-	200	-26	0	0	0	6

Из табл. 2 видно, что опорный план в базисе векторов A₃, A₄, A₂  неоптимальный. Опорный план можно улучшить, если ввести в базис вектор A₁. В этом случае из базиса надо удалить вектор A₄. В результате перехода к новому базису (табл.3) получаем оптимальное опорное решение нецелочисленной задачи ЛП.

Таблица 3

	№	Базис	Сбаз	A0	2	8	2	0	0
					A1	A2	A3	A4	A5
	1	A3	2	84	0	0	1	4/5	12/5
	2	A1	2	16/3	1	0	0	1/5	-1/15
	3	A2	8	20	0	1	0	2/5	1/5
	4	-	-	1016/3	0	0	0	26/5	94/15

Первая компонента опорного решения  нецелая, строим по этой компоненте отсечение согласно (8): . Добавив дополнительную переменную , превратим неравенство в равенство: . Добавив это условие к табл. 3, переходим к табл. 4. Назовем эту задачу ЛП₁. В табл. 4 в столбце A₀ содержится отрицательная компонента, и, следовательно, компоненты вектора A₀ являются компонентами псевдоплана.

Таблица 4

	№	Баз.	Сб	A0	2	8	2	0	0	0
					A1	A2	A3	A4	A5	A6
	1	A3	2	84	0	0	1	4/5	12/5	0
	2	A1	2	16/3	1	0	0	1/5	-1/15	0
	3	A2	8	20	0	1	0	2/5	1/5	0
	4	A6	0	-1/3	0	0	0	-1/5	“-14/15”	1
				1016/3	0	0	0	26/5	94/15	0

Чтобы найти опорное решение, воспользуемся алгоритмом двойственного симплексного метода, согласно которому выводим из базиса вектор A₆ и вводим вектор A₅. Выполнив необходимые вычисления, получаем симплекс-табл. 5, вектор A₀ которой содержит оптимальный опорный план задачи ЛП₁. Среди компонент оптимального решения выбираем компоненту с наибольшей дробной частью, она находится в 3-й строке симплекс-табл. 5. По этой строке строим отсечение по формуле (8):

.

Таблица 5

	№	Баз.	Сб	A0	2	8	2	0	0	0
					A1	A2	A3	A4	A5	A6
	1	A3	2	167/2	0	0	1	1/2	0	3/2
	2	A1	2	75/14	1	0	0	3/14	0	-1/14
	3	A2	8	279/14	0	1	0	5/14	0	3/14
	4	A5	0	5/14	0	0	0	3/14	1	-15/14
				2360/7	0	0	0	30/7	0	32/7

Добавив равенство отсечение к табл. 5, получим новую задачу ЛП₂, представленную симплекс-табл. 6. Согласно двойственному симплексному методу в табл.6 выводим вектор A₇ и вводим в базис вектор A₄.

Таблица 6

	№	Баз.	Сб	A0	2	8	2	0	0	0	0
					A1	A2	A3	A4	A5	A6	A7
	1	A3	2	167/2	0	0	1	1/2	0	3/2	0
	2	A1	2	75/14	1	0	0	3/14	0	-1/14	0
	3	A2	8	279/14	0	1	0	5/14	0	3/14	0
	4	A5	0	5/14	0	0	0	3/14	1	-15/14	0
	5	A7	0	-13/14	0	0	0	“-5/14”	0	-3/14	1
				2360/7	0	0	0	30/7	0	32/7	0