Karmazin_-_Teoria_Igr_Uchebnik / P5_3
.DOCТема 5. РЕШЕНИЕ ЗАДАЧ ДРОБНО-ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
Рассматривается задача: максимизировать дробно-линейную функцию
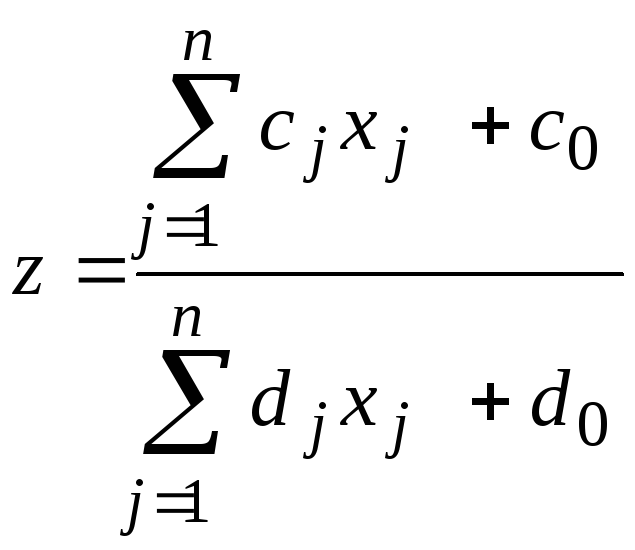, (1)
при условиях
(2)
(3)
Очевидно, что в
области допустимых решений (2) – (3)
выражение
(в противном случае
) ,
т.е. знаменатель целевой функции сохраняет постоянный знак. Будем считать его положительным. Обозначим
(4)
и введем новые переменные
. (5)
В новых переменных задача (1) (3) примет вид: максимизировать
(6)
при условиях
, (7)
, (8)
. (9)
Получили задачу линейного программирования, которая может быть решена обычным симплекс-методом.
Из оптимального
решения
задачи
(6)
(9) при
получаем, с помощью соотношений (5),
оптимальное решение исходной задачи.
В случае, когда
,
имеем
,
откуда следует неограниченность области.
В этом случае максимум
(конечный или бесконечный) достигается
в бесконечно удаленных точках.
Пример 1. Решить следующую задачу дробно-линейного программирования:
Обозначив
перейдем к решению следующей задачи линейного программирования:
Для образования
исходного опорного решения введем лишь
одну искусственную переменную
в последнее уравнение. После этого
заполняем исходную симплекс таблицу и
приступаем к выполнению итераций.
После трех итераций,
табл. 1 , получаем оптимальное решение
Таблица
1
|
|
№ |
Базис |
Сбаз |
B |
0 |
2 |
-1 |
0 |
0 |
-M |
|
|
|
|
|
|
A0 |
A1 |
A2 |
A3 |
A4 |
A5 |
|
|
1 |
A3 |
0 |
0 |
-2 |
1 |
-2 |
1 |
0 |
0 |
|
|
2 |
A4 |
0 |
0 |
-6 |
2 |
1 |
0 |
1 |
0 |
|
¬ |
3 |
A5 |
-M |
1 |
"1" |
1 |
2 |
0 |
0 |
1 |
|
|
4 |
- |
- |
0 |
0 |
-2 |
1 |
0 |
0 |
0 |
|
|
5 |
- |
- |
-1 |
-1 |
-1 |
-2 |
0 |
0 |
0 |
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
¬ |
1 |
A3 |
0 |
2 |
0 |
"3" |
2 |
1 |
0 |
|
|
|
2 |
A4 |
0 |
6 |
0 |
8 |
13 |
0 |
1 |
|
|
|
3 |
A0 |
0 |
1 |
1 |
1 |
2 |
0 |
0 |
|
|
|
4 |
- |
- |
0 |
0 |
-2 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
A1 |
2 |
2/3 |
0 |
1 |
2/3 |
1/3 |
0 |
|
|
|
2 |
A4 |
0 |
2/3 |
0 |
0 |
23/3 |
-8/3 |
1 |
|
|
|
3 |
A0 |
0 |
1/3 |
1 |
0 |
4/3 |
-1/3 |
0 |
|
|
|
4 |
- |
- |
4/3 |
0 |
0 |
7/3 |
2/3 |
0 |
|
В соответствии с формулами (5) находим оптимальное решение исходной задачи
Задание.
В задачах
5.1 – 5.105 максимизировать Z
при неотрицательных
удовлетворяющих приведенным равенствам.
5.1
Z= ; .
5.2
Z= ; .
5.3
Z= ; .
5.4
Z= ; .
5.5
Z= ; .
5.6
Z= ; .
5.7
Z= ; .
5.8
Z= ; .
5.9
Z= ; .
5.10
Z= ; .
5.11
Z= ; .
5.12
Z= ; .
5.13
Z= ; .
5.14
Z= ; .
5.15
Z= ; .
5.16
Z= ; .
5.17
Z= ; .
5.18
Z= ; .
5.19
Z= ; .
5.20
Z= ; .
5.21
Z= ; .
5.22
Z= ; .
5.23
Z= ; .
5.24
Z= ; .
5.25
Z= ; .
5.26
Z= ; .
5.27
Z= ; .
5.28
Z= ; .
5.29
Z= ; .
5.30
Z= ; .
5.31
Z= ; .
5.32
Z= ; .
5.33
Z= ; .
5.34
Z= ; .
5.35
Z= ; .
5.36
Z= ; .
5.37
Z= ; .
5.38
Z= ; .
5.39
Z= ; .
5.40
Z= ; .
5.41
Z= ; .
5.42
Z= ; .
5.43
Z= ; .
5.44
Z= ; .
5.45
Z= ; .
5.46
Z= ; .
5.47
Z= ; .
5.48
Z= ; .
5.49
Z= ; .
5.50
Z= ; .
5.51
Z= ; .
5.52
Z= ; .
5.53
Z= ; .
5.54
Z= ; .
5.55
Z= ; .
5.56
Z= ; .
5.57
Z= ; .
5.58
Z= ; .
5.59
Z= ; .
5.60
Z= ; .
5.61
Z= ; .
5.62
Z= ; .
5.63
Z= ; .
5.64
Z= ; .
5.65
Z= ; .
5.66
Z= ; .
5.67
Z= ; .
5.68
Z= ; .
5.69
Z= ; .
5.70
Z= ; .
5.71
Z= ; .
5.72
Z= ; .
5.73
Z= ; .
5.74
Z= ; .
5.75
Z= ; .
5.76
Z= ; .
5.77
Z= ; .
5.78
Z= ; .
5.79
Z= ; .
5.80
Z= ; .
5.81
Z= ; .
5.82
Z= ; .
5.83
Z= ; .
5.84
Z= ; .
5.85
Z= ; .
5.86
Z= ; .
5.87
Z= ; .
5.88
Z= ; .
5.89
Z= ; .
5.90
Z= ; .
5.91
Z= ; .
5.92
Z= ; .
5.93
Z= ; .
5.94
Z= ; .
5.95
Z= ; .
5.96
Z= ; .
5.97
Z= ; .
5.98
Z= ; .
5.99
Z= ; .
5.100
Z= ; .
5.101
Z= ; .
5.102
Z= ; .
5.103
Z= ; .
5.104
Z= ; .
5.105
Z= ; .