Распределение случайных отклонений при измерении величин

Если повторять измерение некоторой величины многократно, обнаруживается, что в силу разнообразных внешних причин результаты опытов точно не воспроизводятся.

Например, стрелок делает пробоины, смещенные от центра мишени в результате ошибок в прицеливании и определении моментов спуска курка. При этом до выстрела невозможно предсказать его величину и направление, т.е. они случайны. Однако, при рассмотрении мишени после достаточно большой серии выстрелов обнаруживается некоторая закономерность в расположении пробоин: вокруг центра мишени они располагаются гуще и (если стрелок не делает систематических, повторяющихся ошибок) картина распределения пробоин одинакова во всех направлениях.

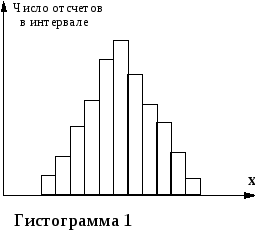
Для наглядного представления распределения значений случайной величины можно построить гистограмму.

Для этого весь диапазон измеренных значений разбивают на разные интервалы и подсчитывают, сколько раз измеряемая величина попадает в каждый из них. Высота каждого из столбцов гистограммы пропорциональна количеству попаданий измеряемой величины в соответствующий диапазон.

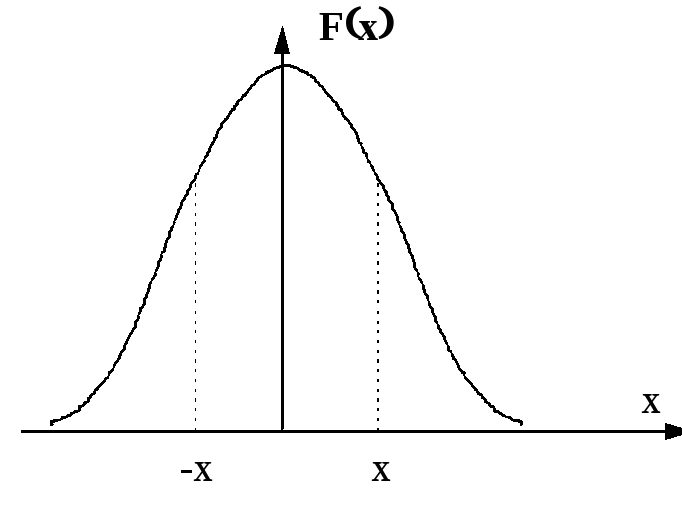
Если увеличить число измерений, а ширину интервалов сделать очень малой (насколько позволяет чувствительность измерительного прибора), гистограмму можно будет заменить плавным графиком ‑ кривой распределения. На вертикальной оси теперь можно откладывать не само число измерений в интервале x, а значение функции x), смысл которой состоит в том, что произведение ее на ширину интервала x дает долю числа отсчетов, приходящихся на этот интервал, т.е. вероятность того, что отдельное, случайно выбранное значение измеряемой величины окажется в интервале от x до x + x .

Функция x), таким образом, есть плотность вероятности, т.е. отношение вероятности нахождения измеряемой величины в бесконечно малом интервале к ширине этого интервала:

.

Для нужд статистической обработки измерений, а также для планирования эксперимента необходимо знать функцию плотности вероятности в аналитической форме, в виде уравнения. Такую задачу не всегда удается решить, но в большинстве случаев можно подобрать в качестве удовлетворительной аппроксимации какое- либо из известных распределений.

Очевидно, что для нахождения вероятности dP попадания измеряемой величины в интервал от x-x до x+x необходимо найти интеграл:

.

Наиболее распространенным следует считать нормальное распределение Гаусса, представляющее собой функцию вида

,

где h ‑ мера точности;  ‑ среднеквадратичное отклонение, связанные соотношениями:

; ,

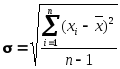где n ‑ число измерений.

Кривой нормального распределения Гаусса можно воспользоваться для расчета вероятности P попадания результата измерения в интересующий нас интервал x. Для этого необходимо взять интеграл:

.

Распределение Стьюдента

При малом числе (от 5 до 20) измерений принято рассчитывать доверительный интервал, используя частный случай распределения Гаусса - распределение Стьюдента. Не описывая теоретических подробностей, приведем лишь порядок обработки результатов измерений для этого случая.

1. Выполнить измерения, число которых n должно быть не менее пяти.

2. Вычислить приближенное среднее значение изn измерений:

3. Найти погрешности отдельных измерений (отклонения от среднего) x_i:

.

4. Вычислить квадраты отклонений .

5. Определить среднее квадратичное отклонение среднего результата:

.

6. Выбрать надежность (вероятность) P и по таблице найти коэффициент Стьюдента t, соответствующий выбранной надежности P и количеству измерений n.

7. Найти границы доверительного интервала x, т.е. погрешность результата измерений: .

8. Сравнить величину погрешности измерений с приборной погрешностью, рассчитанной для однократного измерения.

9. Если x превосходит величину приборной погрешности, что указывает на достаточную точность измерений, рассчитать относительную погрешность результата серии измерений по формуле:

.

10. Записать окончательный результат в виде:

, P, .

Например: R = 8,25  0,20 Дж/моль^.К, P = 0,9,  = 2%.

Превышение доверительного интервала над приборной погрешностью указывает на то, что использовавшиеся приборы не в состоянии обеспечить заданную надежность. В этом случае рекомендуется заменить приборы более точными или, выбрав в качестве доверительного интервала приборную погрешность, рассчитать необходимое при имеющихся приборах число намерений.

Существует оценочный способ проверки качественного выполнения измерения, выяснив, связана ли полученная погрешность измерений с приборной погрешностью, обусловленной конструкцией использованных приборов, или экспериментатором была внесена погрешность из-за неумелого обращения с измерительными приборами и собственной невнимательности.

Для этого необходимо рассчитать суммарную приборную погрешность измерительной установки  и решить обратную задачу: по заданному доверительному интервалу х, равному , найти коэффициент Стьюдента и затем по таблице коэффициентов Стьюдента для количестваn выполненных измерений, найти надежность P. При полученном значении P, лежащем в интервале от 0,7 до 0,99 можно сделать вывод о том, что экспериментатор не внес в процесс измерений дополнительной собственной погрешности и добился максимально возможной точности на использованных им измерительных приборах.