
ЭВМ лекции
.pdf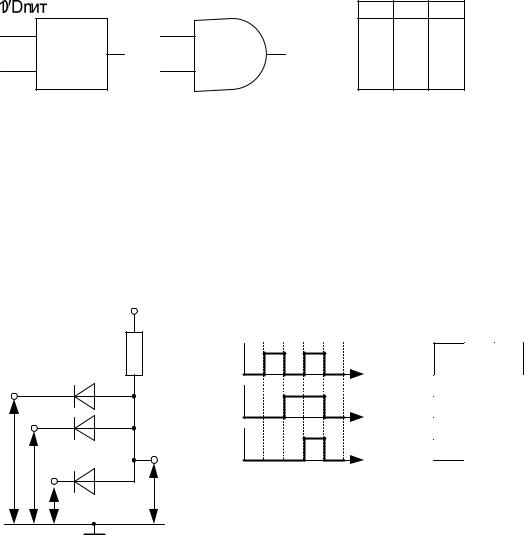
Элемент И (AND) (логическое умножение): на выходе имеет логическую 1 только в том случае, если на все входы подается 1.
Логический элемент И имеет несколько входов и один выход и выполняет операцию логического умножения (конъюнкции):
y=x1 x2 |
y=x1 x2 ... |
xn |
Функция y=0, если хотя бы один из ее аргументов равен нулю, и y=1, если все аргументы равны 1. Упрощенная схема логического элемента И, его таблица истинности и временные диаграммы представлены на рис.7.
Рисунок 7
Микросхемы, содержащие элемент И:
КМОП (ТТЛ): 4081 (7408) – 4 2-входовых элемента 4073 (7411) – 3 3-входовых элемента 4082 (-) – 2 4-входовых элемента
31
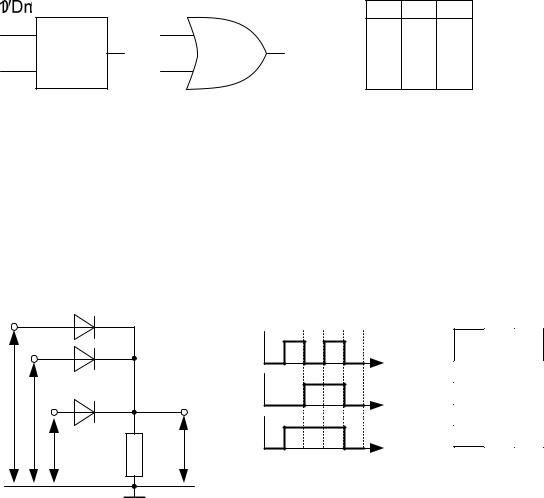
Элемент ИЛИ (OR) (логическое сложение): на выходе имеет логическую 1, если хотя бы на один из входов подается 1.
Логический элемент ИЛИ имеет несколько входов и один выход и выполняет операцию логического сложения (дизъюнкции):
y= x1 x2 |
y=x1 x2 ... |
xn |
Функция y=1, если хотя бы один из ее аргументов равен 1, и y=0, если все аргументы равны 0. Упрощенная схема логического элемента ИЛИ, его таблица истинности и временные диаграммы представлены на рис.8.
Рисунок 8
Микросхемы, содержащие элемент ИЛИ:
КМОП (ТТЛ): 4071 (7432) – 4 2-входовых элемента 4075 (-) – 3 3-входовых элемента 4072 (-) – 2 4-входовых элемента
32
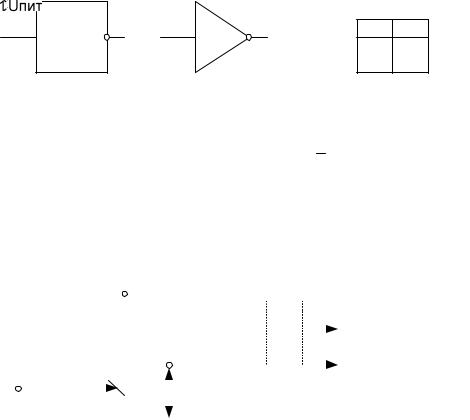
Элемент НЕ (NOT) (логическое отрицание) – инвертор: одновходовое устройство, логическое состояние выхода которого противоположно (комплементарно) логическому состоянию входа).
Логический элемент НЕ имеет один вход и один выход и выполняет
операцию инверсии (отрицания):
y= x.
Функция y=1, если сигнал x=0, и наоборот, y=0, если x=1. Упрощенная схема логического элемента НЕ, его таблица истинности и временные диаграммы представлены на рис.9.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 6 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Микросхемы, содержащие элемент НЕ: |
|||||||||||||||||||
КМОП (ТТЛ): |
|
|
4069, 40106 (7404, 7405, 7414) 6 элементов |
||||||||||||||||
33
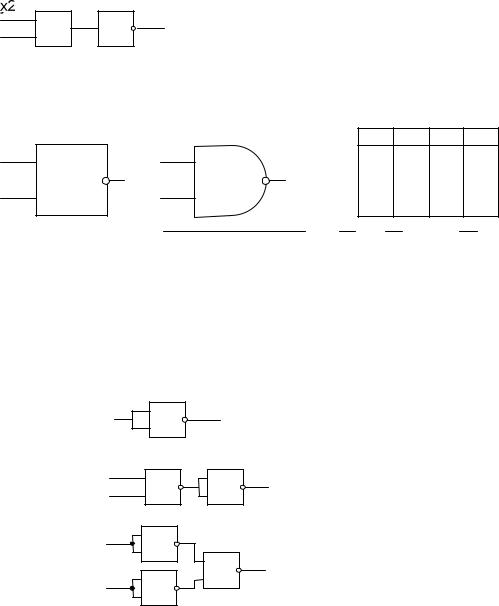
Элемент И-НЕ (NAND) можно представить комбинацией элементов И и НЕ:
На выходе элемент И-НЕ имеет логический 0 только в том случае, если на все входы подается 1.
y=x1 x2 ...xn = x1 x2 ...xn
Функция y=0, если все ее аргументы равны 1, и y=1, если хотя бы один аргумент равен 0.
Элемент И-НЕ является базисным, т.е. на его основе можно получить все 3 основные логические функции:
НЕ:
И:
ИЛИ:
Микросхемы, содержащие элемент И-НЕ:
КМОП (ТТЛ): 4093 (7401, 7439) – 4 2-входовых элемента 4023 (7410) – 3 3-входовых элемента
4012 (7440, 7413) – 2 4-входовых элемента
4068 (7430) – 1 8-входовый элемент
34
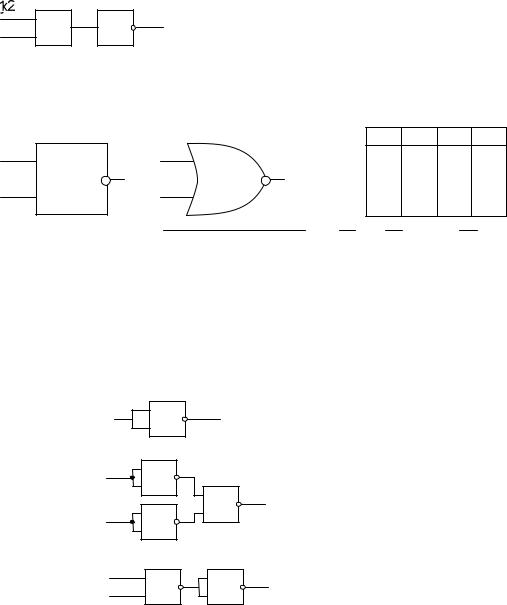
Элемент ИЛИ-НЕ (NOR) можно представить комбинацией элементов ИЛИ и
НЕ:
Элемент ИЛИ-НЕ на выходе имеет логическую 1 только в том случае, если на все входы подается 0.
y=x1 x2 ...xn = x1 x2 ...xn
Функция y=1, если все ее аргументы равны 0, и y=0, если хотя бы один аргумент равен 1.
Элемент ИЛИ-НЕ является базисным, т.е. на его основе можно получить все 3 основные логические функции:
НЕ:
И:
ИЛИ:
Микросхемы, содержащие элемент ИЛИ-НЕ:
КМОП (ТТЛ): 4001 (7433, 7402) – 4 2-входовых элемента 4025 (7427) – 3 3-входовых элемента 4002 (7425) – 2 4-входовых элемента 4078 (-) – 1 8-входовый элемент
35
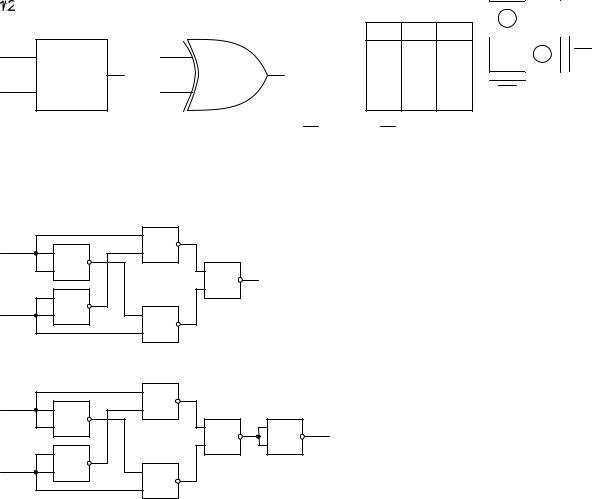
Элемент исключающее ИЛИ (XOR): на выходе имеет логическую 1 только в том случае, если один и только один из входов имеет логическую 1.
В общем случае функция n логических переменных равна 1, если количество единиц в ее входном наборе нечетно.
Элемент реализует функцию y =(x1 x2) (x2 x1).
На рассмотренных выше логических элементах данная функция может быть реализована как
в базисе И-НЕ
в базисе ИЛИ-НЕ
Микросхемы, содержащие элемент исключающее ИЛИ:
КМОП (ТТЛ): 4030, 4070 (7486, 74136) – 4 2-входовых элемента
36
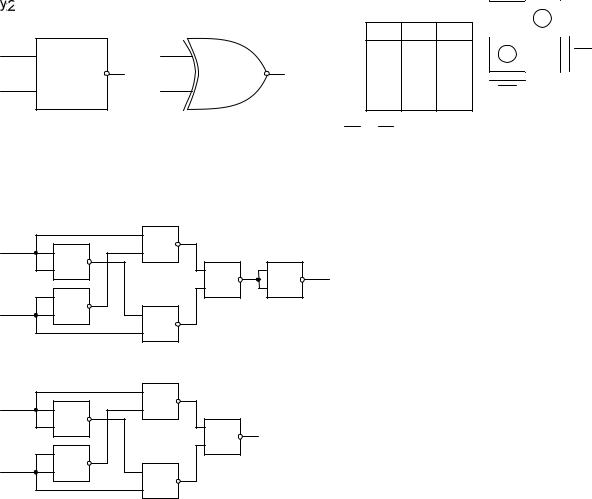
Элемент исключающее ИЛИ-НЕ (XNOR): на выходе имеет логическую 1, если значения входов совпадают.
В общем случае функция n логических переменных равна 1, если количество единиц в ее входном наборе четно.
Элемент реализует функцию y =(x1 x2) (x2 x1).
На рассмотренных выше логических элементах данная функция может быть реализована как
в базисе И-НЕ
в базисе ИЛИ-НЕ
Микросхемы, содержащие элемент исключающее ИЛИ-НЕ: КМОП (ТТЛ): 4077, 4070 (-) – 4 2-входовых элемента
Все функции двух переменных могут быть реализованы в одном из базисов (см. таблицу ниже).
37
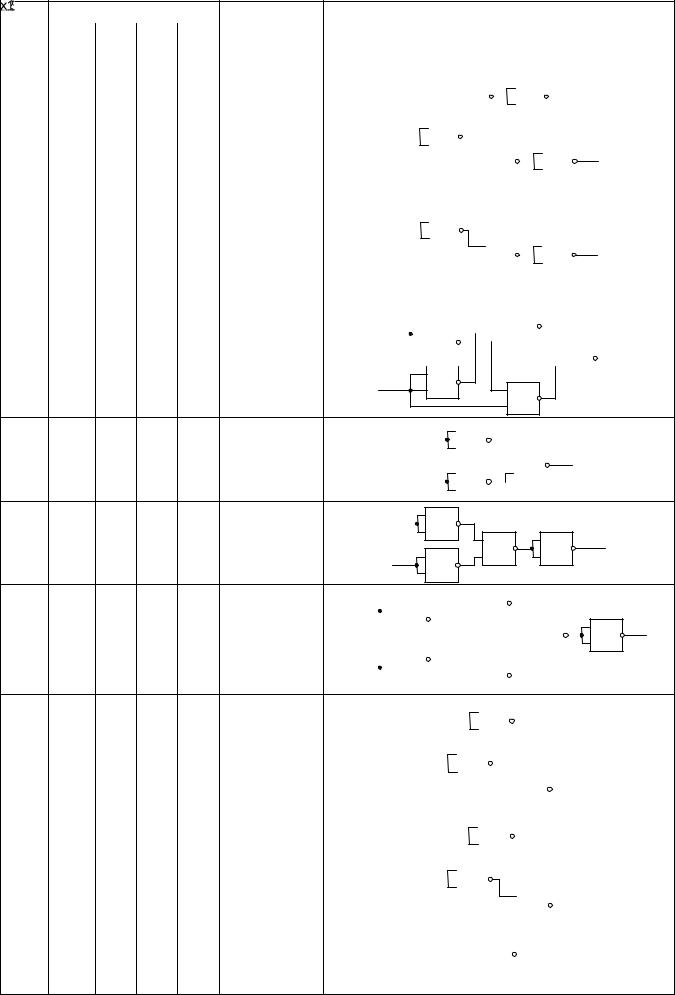
№ |
|
x2 x1 |
|
функция |
|
|
|
|
Схема реализации |
||||||||||||||||||||||||||||||
00 |
01 |
10 |
11 |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
1 |
|
x2x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
0 |
1 |
0 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
0 |
0 |
1 |
1 |
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0 |
1 |
0 |
0 |
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5 |
0 |
1 |
0 |
1 |
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6 |
0 |
1 |
1 |
0 |
x1 |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x2 |
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
0 |
1 1 1 |
x1 x2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 1 |
0 0 0 |
x2 |
|
x1 |
11 1 |
0 0 1 x2x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 |
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
0 |
1 |
0 |
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
13 |
1 |
0 |
1 |
1 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
14 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
15 |
1 |
1 |
0 |
1 |
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
16 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
17 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
+Uпит |
|
|
|||||||||||||
38
8. Дешифраторы
Дешифратором называется комбинационная схема, имеющая n входов и 2n
выходов и преобразующая двоичный код на своих входах в унитарный код на выходах. Унитарным называется двоичный код, содержащий одну и только одну единицу, например 00100000. Таким образом, функция алгебры логики на каждом выходе дешифратора представляет собой конституенту 1 Ki(X) n переменных, где X = xn–1xn–2…x0 – двоичный код набора входных переменных, i = 0, 1, 2,…,2n–1..
Дешифратор, в котором каждому коду наборов входного сигнала соответствует выходной сигнал, равный единице, только на одном выходе, называется полным. Дешифратор может быть и неполным, реализующим только m < 2n конституент 1.
Инверсным называется дешифратор, на выходах которого в любой момент времени присутствует один и только один ноль.
Условное описание дешифратора задается формулой n×m (n на m), для полного дешифратора это формула n×2n. Примерами полных являются дешифраторы КМОП(ТТЛ):
2×4 – 4555, 4556-инверсный (74155 – инверсный) (2 в корпусе) 3×8 – (74137– инверсный, 74138– инверсный)
4×16 – 4514, 4515-инверсный (74154 - инверсный, 74159 – инверсный) 4×10 – 4028 (7442-инверсный, 74142-инверсный)
УГО дешифратора 3×8 приведено на рисунке 8.1.
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DC |
|
|
|
Входы |
|
|
|
|
|
|
Выходы |
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
2 |
|
1 |
|
0 |
0 |
1 |
|
2 |
|
3 |
4 |
5 |
6 |
7 |
||
|
|
|
2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
0 |
|
0 |
|
0 |
1 |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
||
|
|
1 |
|
3 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
0 |
|
1 |
0 |
1 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
||
|
|
2 |
|
4 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
1 |
|
0 |
0 |
0 |
|
1 |
|
0 |
0 |
0 |
0 |
0 |
||
|
|
|
|
5 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
1 |
0 |
0 |
|
0 |
|
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
1 |
|
0 |
|
0 |
0 |
0 |
|
0 |
|
0 |
1 |
0 |
0 |
0 |
|
|
|
|
|
7 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
1 |
|
0 |
|
1 |
0 |
0 |
|
0 |
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||||||
|
Рисунок 8.1 |
|
1 |
|
1 |
|
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
1 |
0 |
||||
|
|
1 |
|
1 |
|
1 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Номер |
разряда, в котором |
|
устанавливается |
«1» на |
выходе |
дешифратора, |
|||||||||||||||
определяется кодом на его входах (см. таблицу истинности):
39
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y0 = x2x1x0 |
y1 = x2x1x0 |
y2 = x2x1x0 |
y3 = x2x1x0 |
||||||||||||
y4 = x2 |
|
|
|
y5 = x2 |
|
x0 |
y6 = x2x1 |
|
y7 = x2x1x0 |
||||||
x1 |
x0 |
x1 |
x0 |
||||||||||||
Среди неполных дешифраторов наибольшее распространение получили дешифраторы 4×10: 4028 (7442– инверсный, 74141– инверсный), комбинация на входе которых соответствует одной из набора десятичных цифр.
Схемотехнически дешифратор представляет собой совокупность конъюнкторов (или элементов И-НЕ в дешифраторах с инверсными выходами), не связанных между собой. Каждый конъюнктор (или элемент И-НЕ) вырабатывает одну из выходных функций.
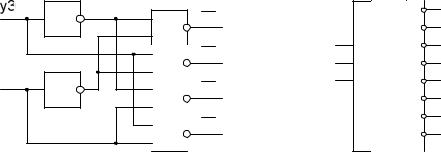
На рис.8.2 представлена схема формирования выходных сигналов для полного инверсного двоичного дешифратора 2×4. В большинстве реальных интегральных микросхем реализованы дешифраторы с инверсными выходами. Обозначение такого дешифратора показано на рис.8.2.
DC |
0 |
1 |
|
0 |
2 |
1 |
3 |
2 |
4 |
|
5 |
|
6 |
|
7 |
Рисунок 8.2 Схема дешифратора 2х4 и УГО дешифратора с инверсными выходами
Логику преобразования выполняют элементы И-НЕ, в то время как элементы НЕ служат для получения инверсии входных сигналов.
На выходах дешифратора с инверсными входами образуется унитарный код, содержащий один и только один ноль. Например, если входные сигналы имеют значение 1102=610, то выходы дешифратора, представленного на рис.8.2, будут находиться в состоянии 10111111, то есть выход 6 будет иметь значение, отличное от остальных выходов.
Дешифраторы широко применяются в различных устройствах компьютеров. Прежде всего, они используются для выбора ячейки запоминающего устройства, к которой производится обращение для записи или считывания информации. При этом часть разрядов адресного кода может формироваться дешифраторами,
40
