1. Объем цилиндрического бруса. Двойной интеграл, теорема существования, свойства.

Двойной интеграл вводится рассмотрением задачи о вычисление V криволинейного цилиндра. Для определения объёма параллелепипеда на которые мы разбили цилиндр: Δs_i*f(x_i,y_i)≈ΔV_i, точное значение V криволинейного цилиндра определяется разбиением области D на ∞ число частей с ∞ малыми размерами V=lim_ΔS→0 ∑_i=1 f(x_i,y_i)ΔS_i. Выражение стоящее справа от равенства представляет собой двойной интеграл от f(x,y) ∫∫_d f(x,y)dS=lim_ΔS→0 ∑_i=1 f(x_i,y_i)ΔS_i. Свойства: 1) ∫∫_d dS=S_d; 2) Пусть задана поверхностная плотность пластины в виде функции α(x,y) тогда m: m=∫∫_d α(x,y)dS; 3) ∫∫_d f(x,y)dS=V - объём криволинейного цилиндра ограниченная z=f(x,y); 4)5)6)если область D можно разбить на подобласти D1,D2… тогда Теорема существования: Для всякой непрерывной функции f(x,y) в ограниченной замкнутой области D существует двойной интеграл: ∫∫_D f(x,y)ds = lim_n→∞ ∑_i=1 f(x_i,y_i)ΔS_i.

2. Вычисление двойного интеграла в декартовой системе координат. Изменение порядка интегрирования в повторном интеграле.

Для вычисление двойного интеграла необходимо разбить область D прямыми параллельными осями координат Х и У: ∫∫_d f(x,y)dS=∫∫_d f(x,y)dxdy. Область D называется правильной в направление оси Оx(Оy) если любая прямая параллельная оси ОХ(оси ОУ) пересекают границу L области D не более двух раз. Любую неправильную область можно разбить на сов. Правильных областей.

1) Область правильная в направление оси Оy: ∫∫_d f(x,y)dxdy=∫_a^b dx ∫_φ1(x)^φ2(x) f(x,y)dy.

2) Область D является правильной в направление оси Оx: ∫∫_d f(x,y)dxdy=∫_c^d dy ∫_ψ1(x)^ψ2(x) f(x,y)dx. Выражение стоящее справа от равенства 1 и 2 называется повторными интегралами.

3) Область D является правильной и в направление Ох и Оу, то ∫_a^b dx ∫_φ1(x)^φ2(x) f(x,y)dy = ∫_c^d dy ∫_ψ1(x)^ψ2(x) f(x,y)dx, переход от левой части равенства 3 и обратно называется изменением порядка интегрирование в повторном интеграле.

3. Замена переменных в двойном интеграле. Преобразование двойного интеграла к полярным координатам и обобщенным полярным.

Пусть переменные Х и У связаны с переменными U и V соотношениями x=φ(U,V), y=ψ(U,V), где φ(U,V) и ψ(U,V) взаимно отражают область D плоскости Оху на область D` в плоскости O`uv. При этом Якобиан сохраняет постоянный знак в областиD тогда будет иметь вид: .

Рассматривая переход от декартовых координат к полярным: x=pcosφ, y=psinφ. dx/dS=cosφ, dx/dφ=-psinφ, dy/dP=sinφ, dy/dφ=pcosφ.

Различные расположения полюса О и области D: 1) Полюс О находится вне области D: ∫∫_d f(x,y)dxdy=∫_α^β dφ ∫_p1(φ)^p2(φ) f(pcosφ, psinφ)pdp.

2) Полюс О находится внутри области D: ∫∫_d f(x,y)dxdy=∫₀^p(φ) f(pcosφ, psinφ)pdp. 3) Полюс О находится на границе области D: ∫∫_d f(x,y)dxdy=∫_α^β dφ ∫₀^p(φ) f(pcosφ, psinφ)pdp.

4.Геометрические приложения двойного интеграла. Вычисление объемов и площадей поверхности Площадь плоской фигуры: Если f (x,y)=1 в интеграле ∫∫_R f(x,y)dxdy, то двойной интеграл равен площади области интегрирования R.  Площадь области типа I (элементарной относительно оси Оy) выражается через повторный интеграл в виде A=∫_a^b∫_g(x)^f(x)dydx.

Объем тела: Если f (x,y) > 0 в области интегрирования R, то объем цилиндрического тела с основанием R, ограниченного сверху поверхностью z = f (x,y), выражается формулой V=∫∫_R f(x,y)dA.

Площадь поверхности

Предположим, что поверхность задана функцией z = f (x,y), имеющей область определения R. Тогда площадь такой поверхности над областью z определяется формулой S=∫∫_R sqrt(1+(∂z/∂x)²+(∂z/∂y)²)dxdx при условии, что частные производные ∂z/∂x и ∂z/∂y непрерывны всюду в области R. 

Площадь и объем в полярных координатах. Пусть S является областью, ограниченной линиями θ=α, θ=β, r=h(θ), r=g(θ). Тогда площадь этой области определяется формулой

Объем тела, ограниченного сверху поверхностью z=f(r,θ) с основанием S, выражается в полярных координатах в виде V=∫∫_S f(r,θ)rdrdθ.

5.Масса неоднородного тела. Тройной интеграл. Свойства.

Тройной интеграл вводится рассмотрением задачи о вычисление массы произвольной формы. Пусть функция U=f(x,y,z) задаем распределение плотности тела располагающая в области V. Разбиваем область В произвольными поверхностями на n x частей ΔV_i (i=1,n). Выбираем произвольным образом в каждом элементе точку . Равенство в последней формуле достигается при бесконечно большом разбиение в бесконечно малыеV эл.

Отличительные свойства: 1) ∫∫∫_V dV=V – Объем области интегрирования

2) если f(x,y,z)=p(x,y,z), тогда ∫∫∫_V p(x,y,z)dV=m.

6)Вычисление тройного интеграла.

Рассмотрим область интегрирования U ограничена снизу поверхностью z = φ1(x,y), а сверху – поверхностью а сверху - поверхностью z = φ ₂(x,y)

V: a≤x≤b

φ₁(x)≤y≤φ₂(x)

ψ₁(x,y)<z≤ψ₂(x,y)

∫∫∫_V d(x,y,z)dV=∫∫∫_V f(x,y,z)dxdydz=∫_a^b dx ∫_φ1(x)^φ2(x) dy ∫_ψ1(x)^ψ2(x) f(x,y,z)dz

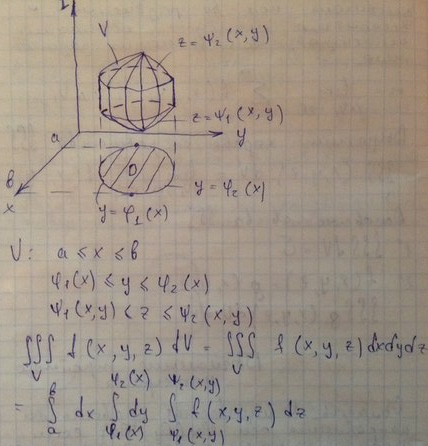
15. Числовые ряды. Сходимость числового ряда. Необходимый признак сходимости.

Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).

Числовым рядом называется выражение вида: u₁+u₂+…+u_n+…=∑u_n.

u₁+u₂+…+u_n+… – члены числового ряда.

u_n – общий член числового ряда.

Теорема 1 (необходимый признак сходимости ряда): Если числовой ряд сходится, то предел lim u_n=0, обратное утверждение неверно.

Теорема 2: Если предел lim u_n=a≠0, то числовой ряд расходится.

Теорема 3 (признаки сравнения): Если даны два ряда u₁+u₂+…+u_n+… и v₁+v₂+…+v_n+… и для всех n>n₀ выполняется 0<u_n<=v_n.

Из сходимости ряда v₁+v₂+…+v_n+… следует, что ряд u₁+u₂+…+u_n+… сходится.

Из расходимости ряда u₁+u₂+…+u_n+… следует, что что ряд v₁+v₂+…+v_n+… расходится.

В качестве рядов для сравнения обычно берут ряд, составленный из членов геометрической прогрессии и гармонический ряд.

Теорема 4 (предельный признак сравнения, следствие из теоремы 3): Если ряды u₁+u₂+…+u_n+… и v₁+v₂+…+v_n+… с положительными членами таковы, что существует предел lim u_n/v_n=a≠0≠∞, то оба ряда либо сходятся, либо расходятся.

16. Признак сравнения и предельный признак сравнения для рядов с положительными членами. Признаки сходимости Даламбера и Коши. Интегральный признак сходимости.

Признак сравнения: Если даны два ряда u1+u2+…+un+… и v1+v2+…+vn+… и для всех n>n0 выполняется 0<un<=vn.

Из сходимости ряда v1+v2+…+vn+… следует, что ряд u1+u2+…+un+… сходится.

Из расходимости ряда u1+u2+…+un+… следует, что что ряд v1+v2+…+vn+… расходится.

В качестве рядов для сравнения обычно берут ряд, составленный из членов геометрической прогрессии и гармонический ряд.

Предельный признак сравнения: Если ряды u1+u2+…+un+… и v1+v2+…+vn+… с положительными членами таковы, что существует предел lim un/vn=a≠0≠∞, то оба ряда либо сходятся, либо расходятся.

Признак Даламбера: Пусть для ряда u₁+u₂+…+u_n+… u_n>0, начиная с n>n₀ предел lim u_n+1/u_n=q

1)q<1 – ряд сходится 2)q>1 – ряд расходится 3)q=1 – нет ответа

Радикальный признак Коши: Если для ряда u₁+u₂+…+u_n+… u_n+…>0, для всех n>n₀ предел lim u_n^1/n=q

1) q<1 – ряд сходится 2)q>1 – ряд расходится 3)q=1 – нет ответа

Интегральный признак Коши: Пусть члены ряда u₁+u₂+…+u_n+… u_n+… монотонно убывают и y=f(x) непрерывна при x≥a≥1 таковы, что f(n)=u_n, тогда ряд u₁+u₂+…+u_n+… u_n+… и интеграл ∫f(x)dx либо одновременно сходятся, либо одновременно расходятся.

17. Ряды с произвольными членами. Абсолютная и условная сходимость. Признак Лейбница и оценка остатка знакочередующегося ряда. Теорема Коши об абсолютной сходимости ряда.

Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда является знакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.

Абсолютная и условная сходимость. Ряд ∑u_n называется абсолютно сходящимся, если ряд ∑|u_n| также сходится.

Если ряд ∑u_n сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.

Ряд ∑u_n называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Признак Лейбница. Для знакочередующихся рядом действует достаточный признак сходимости Лейбница. Пусть u_n является числовой последовательностью, такой, что:

1) u_n+1<u_n для всех n;

2) lim u_n=0

Тогда знакочередующиеся ряды ∑(-1)ⁿ*u_n и ∑(-1)^n-1*u_nсходятся.

Оценка остатка. Из доказательства признака Лейбница следует, что сумма знакопеременного сходящегося ряда меньше по модулю первого члена ряда. Поскольку любой остаток ряда u_n является также рядом Лейбница, то для него справедливо: u_n<| u_n+1|.

18. Функциональный ряд. Область сходимости. Понятие равномерной сходимости. Мажорирующий ряд. Признак Вейерштрасса. Свойства равномерно сходящихся рядов (непрерывность суммы, интегрирование и дифференцирование ряда).

Функциональный ряд – это ряд вида: u₁(x)+u₂(x)+…+u_n(x)+…=∑u_n(x).

Ряд u₁(x)+u₂(x)+…+u_n(x)+… называется сходящимся в точке x=x_0, если сходится числовой ряд.

Область сходимости ряда – множество значений X при которых ряд u₁(x)+u₂(x)+…+u_n(x)+… сходится. Область сходимости ряда всегда включается в область сходимости функции.

u₁(x), u₂(x),… сходятся к u_n(x), если для любого ε>0 существует такой номер N_ε, что для всех номеров n>N_ε и всех точек x∈X выполняется неравенство |f_n(x)-f(x)|<ε.

Мажорирующий ряд – это числовой, положительный и сходящийся ряд, в котором для любых n и сразу для всех x из заданного промежутка, все члены заданного ряда меньше по модулю, чем члены мажорирующего ряда, а если больший ряд сходится, то сходится и меньший.

Признак Вейерштрасса. Рассмотрим ряд: ∑u_n(x). Пусть существует последовательность a_n такая, что для любого x∈X выполняется неравенство |u_n(x)|<a_n, кроме того, ряд ∑a_n(x) сходится. Тогда ряд ∑u_n(x) сходится на множестве X абсолютно и равномерно.

Свойства равномерно сходящихся рядов:

1) Теоремы о непрерывности: Рассматриваются комплекснозначные функции на множестве E. Последовательность непрерывных в точке функций сходится к функции, непрерывной в этой точке. Последовательность u_k(x) сходится к u(x) так, что для любого k функция u_k(x) непрерывна в точке x₀. Тогда u(x) непрерывна в x₀.

Ряд непрерывных в точке функций сходится к функции, непрерывной в этой точке.

Ряд ∑u_k(x) сходится к S(x) так, что для любого k функция u_k(x) непрерывна в точке x₀, тогда S(x) непрерывна в x₀.

2) Теоремы об интегрировании: Рассматриваются действительнозначные функции на отрезке действительной оси.

Теорема о переходе к пределу под знаком интеграла: для любого k функция u_k(x) интегрируема на отрезке [a,b]. Если u_k(x) сходится к u(x) на [a,b], тогда ∫u_k(x)dx сходится к ∫u(x)dx для любого x∈[a,b].

Теорема о почленном интегрировании: для любого k функция u_k(x) непрерывна на отрезке [a,b]. Если ∑u_k(x) сходится к S(x) на [a,b], тогда ∑∫u_k(x)dx сходится к ∫S(x)dx для любого x∈[a,b].

3) Теоремы о дифференцировании: Рассматриваются действительнозначные функции на отрезке действительной оси.

Теорема о дифференцировании под пределом: для любого k функция u_k(x) непрерывно дифференцируема на отрезке [a,b], так что существует c∈[a,b]: u_k(c) сходится, u_k’(x) сходится к ω(x) на отрезке [a,b], тогда существует такой u(x) что u_k(x) сходится к u(x), u(x) – непрерывно дифференцируема на [a,b], u’(x)=ω(x) на [a,b].

Теорема о почленном дифференцировании: для любого k функция u_k(x) непрерывно дифференцируема на отрезке [a,b] так, что существует такое c∈[a,b]: ∑u_k(c) сходится, ∑u_k’(x) равномерно сходится на отрезке [a,b], тогда существует такой S(x) при котором ∑u_k сходится к S(x), S(x) – непрерывно дифференцируема на [a,b], S’(x)=∑u_k’(x) на [a,b].

19. Степенные ряды. Теорема Абеля. Интервал и радиус сходимости степенного ряда. Равномерная сходимость. Непрерывность суммы, интегрирование и дифференцирование.

Степенной ряд – функциональный ряд ∑a_n(x-x₀)ⁿ. В частном случае при x₀=0 получается ряд ∑a_nxⁿ. a₁, a₂,…,a_n,… – коэффициенты ряда. x₀ – фиксированное число.

Теорема Абеля. 1) Если степенной ряд ∑a_nxⁿ сходится при некоторых значениях x=x₁≠0, то абсолютно сходится при любых удовлетворяющих неравенству, т.е. |x|<|x₁|. 2) если степенной ряд ∑a_nxⁿ расходится при x=x₂, то он расходится и при любых x удовлетворяющих неравенству |x|>|x₂|.

Интервал сходимости – интервал, в каждой точке которого степенной ряд с действительными членами сходится, причем абсолютно. На каждом из концов этого интервала ряд может как сходиться (абсолютно или условно), так и расходиться.

Радиус сходимости – число R≥0 для которого при |x|<R ряд a_nxⁿ сходится (при |x|>R ряд a_nxⁿ расходится).

a₁(x-x₀) ⁿ, a₂(x-x₀) ⁿ,… сходятся к a_n(x-x₀)ⁿ, если для любого ε>0 существует такой номер N_ε, что для всех номеров n>N_ε и всех точек x∈X выполняется неравенство |f_n(x)-f(x)|<ε.

Непрерывность суммы, интегрирование и дифференцирование.

Теорема 1: Ряд сходится равномерно на каждом отрезке [a,b], строго внутреннем к его промежутку сходимости.

Теорема 2: Сумма степенного ряд непрерывна в каждой внутренней точке его промежутка сходимости.

Теорема 3: Ряд можно интегрировать почленно по любому отрезку [a,b], строго внутреннему к его промежутку сходимости.

Теорема 4: Ряд можно дифференцировать почленно в любой внутренней точке его промежутка сходимости.

Теорема 5: Сумма S(x) степенного ряда в каждой внутренней его точке его промежутка сходимости имеет производные всех порядков. Эти производные могут быть получены дифференцированием степенного ряда.

20. Ряд Тейлора. Разложение функций в ряд Тейлора, Маклорена. Применение степенных рядов к приближенным вычислениям.

Если функция y=f(x) имеет производное в окрестности точки х=x₀ до n+1 порядка (включительно), то существует точка С, которая лежит в окрестности точки x₀, C=x₀+θ(x–x₀), где 0<θ<1. Такая что f(x)=f(x₀)+f(x₀)/x*(x-x₀)+…+f(x_n)/n*(x-x₀)ⁿ+Rn(x) – эта формула называется формулой Тейлора. Rn(x)=f⁽ⁿ⁺¹⁾(c)/(n+1)*(x–x₀)^{n+1 –} остаточный член ряда в форме Лагранжи. В частности при x₀=0 получается ряд Маклорена: f(x)=f(0)+f ’(0)/1*x+f ‘’(x)/2*x²+…+f⁽ⁿ⁾(0)/n*xⁿ+Rn(x); C=θx, где 0<θ<1.

Условие разложимости в ряд Тейлора: Если функция дифференцируема в окрестности m. x₀ любое число до бесконечности раз и в некоторой окрестности этой точки Rn(x) стремится к нулю, при n стремящимся к нулю (lim_n→∞ Rn(x)=0), то f(x)=f(x₀)+f ’(0)/1!*(x–x₀)+…+f⁽ⁿ⁾x₀/n!+…

Степенные ряды приближенных вычислений: 1) вычисление значений функции – Вычисление значений этой функции заключается в отыскании суммы ряда при заданном значении аргумента х. С заданным значение точности. Точность можно установить путем оценивания любого остатка числового ряда, либо остаточного члена в форме Лагранжи. 2) Вычисление интегралов - помощью разложения подынтегральных выражений в степенной ряд можно приблизительно вычислить определенные интегралы. 3) Приближенное значение ДУ - в случае, когда не получается решить ДУ, применяется приближенные методы связанные с разложением функции в степенной ряд. Решение задачи коши ищется в виде ряда Тейлора, производные начиная со 2-ого порядка вычисляются дифференцирование исходного ДУ.