10. Условия независимости криволинейного интеграла от пути интегрирования

Криволинейный интеграл второго рода от векторной функции   F=Pi+Qj+Rk не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция u=u(x,y,z), такая, что F=grad u или ∂u/∂x=P, ∂u/∂y=Q, ∂u/∂z=R.

В этом случае криволинейный интеграл второго рода от функции F вдоль кривой C от точки A до точки B выражается формулой ∫_c F(r)dr=∫_cPdx+Qdy+Rdz=u(B)–u(A).

Таким образом, если криволинейный интеграл не зависит от пути интегрирования, то для любого замкнутого контура C справедливо соотношение ∫_c F(r)dr=0

Векторное поле, обладающее свойством F=grad u, называется потенциальным, а функция u=u(x,y,z) называется потенциалом. 

Признак потенциальности поля: Криволинейный интеграл II рода от функции F=Pi+Qj+Rk не зависит от пути интегрирования, если

Предполагается, что каждый компонент функции F имеет непрерывные частные производные по переменным x, y и z.  Если криволинейный интеграл рассматривается в плоскости Oxy, то в случае потенциального поля будет справедливо соотношение ∫_c Pdx+Qdy=u(B)–u(A).

В этом случае признак потенциальности векторного поля упрощается и принимает вид ∂P/∂y=∂Q/∂x. Рассмотренный признак является необходимым, но, вообще говоря, не достаточным для потенциальности поля. Данное условие достаточно, если только область интегрирования D односвязна. 

9. Задачи, приводящие к криволинейному интегралу 1-го рода. Определение криволинейного интеграла 1-го рода, свойства. Вычисление

Разобьем кривую l на n дуг. Приближенное значение массы m_i дуги Δl_i будет равно

,

Точное значение массы кривой будет равно m=lim_λ→0 ∑_i=1 γ(ξ_i, η_i, ζ_i)Δl_i.

Определение криволинейного интеграла I рода.

Число I называется пределом интегральных сумм I_n(Δl_i,P_i) при λ→0 если для любого ε>0 существует δ>0 такое, что для любого разбиения кривой у которого λ<δ, при любом выборе точекP_i выполняется неравенство |I_n(Δl,P_i)-I|<ε.

Если существует конечный предел интегральных сумм I_n(Δl_i,P_i) при λ→0, то его называют криволинейным интегралом I рода (по длине дуги) от функции f(x,y,z) по кривой l

Если существует ∫_l f(x,y,z)dl, то функция f(x,y) называется интегрируемой по кривой l.

Свойства криволинейного интеграла I рода:

1. ∫_l dl=l, где l – длина кривой l.

2. Постоянный множитель можно выносить за знак криволинейного интеграла I рода, т.е. ∫_l с*f(x,y,z)dl=с*∫_l f(x,y,z)dl. .

3. Криволинейный интеграла I рода от алгебраической суммы двух (конечного числа) функций равен алгебраической сумме криволинейных интегралов I рода от этих функций, т.е.

.

4. Если кривая l разбита на две частиl₁ и l₂, не имеющие общих внутренних точек, то

5. Если всюду на кривой l функция f(x,y,z)>0 (f(x,y,z)≥0), то ∫_l f(x,y,z)dl≥0.

6. Если всюду на кривой l f(x,y,z)<φ(x,y,z) (f(x,y,z)≤φ(x,y,z)), то ∫_l f(x,y,z)dl≤∫_l f(x,y,z)dl

Вычисление криволинейного интеграла I рода

Если функции x=φ(t), y=ψ(t), z=χ(t) имеют на [α;β] непрерывные производные, которые не обращаются в нуль одновременно, то кривая l называется гладкой.

Если функции x=φ(t), y=ψ(t), z=χ(t) имеют на [α;β] кусочно-непрерывные производные, которые не обращаются в нуль одновременно, за исключением конечного числа точек, то кривая l называется кусочно-гладкой.

Теорема 1. Если l – гладкая кривая, заданная уравнениями (2) и функция f(x,y,z) непрерывна на l, то f(x,y,z) интегрируема по кривой l и справедливо равенство

.

21. Ряд Фурье. Условие разложимости функции в тригонометрический ряд Фурье (теорема Дирихле). Разложение в ряд Фурье функций с произвольным периодом, непериодических функций.

Ряд Фурье – Функциональный ряд вида a₀/2+∑_n=1 (a_n*cosnx*b_n*sinnx), где коэффициенты a и b определяются по формулам:

a_n=1/π*∫_–π^π f(x)*cosnxdx (n=0,1,2,…),

b_n=1/ π*∫_–π^π f(x)*sinnxdx (n=1,2,3,…).

Теорема Дирихле: Если функция периодическая с периодом 2π кусочно-монотонная и ограниченная на отрезке [–π,π] то ее ряд Фурье сходится в любой точке и его сумма S(x)=(f(x-0)+f(x+0))/2. Если функция имеет период 2l, то её ряд Фурье записывается в виде: f(x)=a₀/2+∑_n=1 a_n*cos(πnx/l)+b_n*sin(πnx/l),

где коэффициенты a и b определяются по формулам:

a_n=1/l*∫_–l^l f(x)*cos(πnx/l)dx,

b_n=1/l*∫_–l^l f(x)*sin(πnx/l)dx.

24. Определение функции комплексного переменного. Области и их границы. Окрестности. Показательная и логарифмическая функции.

Пусть G область в комплексной плоскости C. Если каждой точке z∈G поставить в соответствие единственное комплексное число w, то говорят, что на области G∈C задана однозначная функция комплексного переменного и обозначается w=f(z). Область G называется областью определения функции, z – аргумент функции, w – значение функции в точке z.

Если каждому z ставится в соответствие несколько значений w, то на области G∈C задана многозначная функция комплексного переменного.

Граница области D – контур по которому вычисляется интеграл от функции f(z).

Фундаментальное понятие окрестности вводится на комплексной плоскости — окрестностью U_z0 точки z₀∈C называется множество вида U_z0={z:|z-z₀|<r}, r>0. Геометрически на комплексной плоскости окрестности имеют вид окружности с центром в определенных точках комплексной плоскости.

Показательная функция: e^z=e^x(cosy+isiny)

Показательная функция комплексного переменного является периодической функцией с основным периодом 2πi, т. е. e^z+2πi=e^z

Логарифмическая функция ln z, при z≠0 определяется как обратная к показательной функции, причем ln z=ln|z|+i(arg z +2πk), k=0,±1,±2,…

Так как показательная функция – периодическая с периодом 2πi, то логарифмическая функция является многозначной. В каждой точке z≠0 она принимает бесконечно много значений. Функция ln z=ln|z|+i arg z, где arg z – главное значение аргумента, называется главным значением логарифмической функции. Итак, ln z=ln z + i2πk, k=0,±1,±2,…

25. Тригонометрические функции комплексного переменного и обратные тригонометрическим. Гиперболические функции. Общая степенная функция.

Значение целой положительной степени комплексного аргумента, значение функции f(z)=zⁿ , проще всего вычислять в тригонометрической форме. Если z=x+iy=r*(cosφ+isinφ), то для любого целого положительного числа n имеет место формула:

w=f(z)=zⁿ=rⁿ(cos(nφ)+isin(nφ)).

Если w=f(z)=f(x+iy)=u(x, y)+iv(x, y), то u(x, y)=rⁿ*cos(nφ), u(x, y)=rⁿ*sin(nφ).

Значения обратных тригонометрических функций комплексного переменного вычисляются по формулам:

f(z)=arcsin z = –i*ln(iz+sqrt(1–z²)),

f(z)=arccos z = –i*ln(iz+sqrt(z²–1)).

Тригонометрические функции комплексного аргумента определяются формулами:

Гиперболические функции комплексного переменного определяются совершенно так же, как функции в действительной области:

Вычисление корня n-й степени из комплексного числа. Если z = x + iy = r(cosφ + isinφ ), то значения функции f(z) = e^z вычисляются по формуле:  f(z) = e^z = e^x+iy = e ^xe ^iy = e^x (cosy + isiny).  Если w = f(z) =  f(x + iy) = u(x, y) + iv(x, y), то u(x,y)=e^x cosy , v(x,y) = e^x siny.

30. Нули аналитической функции. Признак нуля. Порядок нуля.

Пусть функция f (z) является аналитической в точке z₀. Точка z₀ называется нулем функции f(z), если её значение в этой точке равно нулю, т.е. f(z₀) = 0.

В разложении функции в ряд Тейлора в окрестности нуля этой функции (т. z₀) отсутствует свободный член: С₀=f(z₀) = 0.

Признак нуля – бесконечно удалённую точку z=∞ называют нулём функции f(z), если существует предел f(∞)=lim f(z)=0.

Порядок нуля: Если при этом в разложении отсутствуют и слагаемые, содержащие степени разности (z-z₀) до n-ой степени, т.е. разложение имеет вид: f(z)=∑_k=n C_k(z–z₀)^k или f(z)=C_n(z–z₀)ⁿ+C_n+1(z–z₀)ⁿ⁺¹+…, C_n≠0, то точка z₀ называется нулем порядка n функции f(z).

Простой нуль – нуль первого порядка (n = 1).

31. Особые изолированные точки (устранимая, полюс, существенно особая точка). Поведение функции в изолированной особой точке.

Изолированная особая точка — точка, в которой функция f(z) перестаёт быть аналитической. Различают три типа изолированных особых точек:

1) Особая точка называется устранимой, если существует предел в этой точке lim f(z)≠f(z₀), причём lim f(z) конечен.

Разложение функции f(z) в ряд Лорана в окрестности устранимой особой точки имеют только правильную часть.

f(z)=a₀+a₁(z–z₀)+…+a_n(z–z₀)ⁿ+…

2) Особая точка называется полюсом, если предел при z→z₀ равен ∞.

lim f(z)=∞, z₀ – полюс.

Лорановское разложение функции f(z) в окрестности полюса содержит конечное число слагаемых в главной части разложения ряда Лорана.

F(z)=a_m/(z–z₀)^m+a_m+1/(z–z₀)^m+1+…+a₁/(z–z₀)+a₀+…+a_n(z–z₀)ⁿ+…

Максимальное значение степени m множителя (z–z₀) называется порядком полюса при a_-m≠0. Если m=1, то полюс называется простым.

3) Особая точка называется существенно особой, если lim f(z) при z→z₀ не существует.

Лорановское разложение f(z) в окрестности существенно особой точки содержит ∞ число слагаемых.

F(z)=…+a_m/(z–z₀)^m+a_m+1/(z–z₀)^m+1+…+a₀+…+a_n(z–z₀)ⁿ+…

32. Вычеты. Вычет в особых точках. Нахождение вычета в простом полюсе и полюсе порядка m. Вычет функции в бесконечно удаленной точке. Основная теорема о вычетах.

Вычет – объект (число, форма или когомологический класс формы), характеризующий локальные свойства заданного.

Если f(z) является аналитической в некоторой области D, то интеграл по замкнутому контуру C лежащий в области D=0. ∫_C f(z)dz=0.

Если же f(z) не является аналитической, то интеграл по замкнутому контуру C≠0. ∫_C f(z)dz≠0.

Пусть контур С охватывает конечное число полюсов ∫_C f(z)dz=∫_C1 f(z)dz+…+∫_Cn f(z)dzю

Пусть контур C охватывает область содержащую z₀-полюс. Рассмотрим разложение f(z) в окрестности полюса z₀.

f(z)=a_m/(z–z₀)^m+…+a_-1/(z–z₀)+…+a₀+a₁(z–z₀)+a₂(z–z₀)²+…

∫_C f(z)dz=∫_C a_m/(z–z₀)^mdz+…+∫_C a_-1/(z–z₀)dz+…+∫_C a₀dz+∫_C a₁(z–z₀)dz+∫_C a₂(z–z₀)²dz+…=2πia_-1

∫w(z)/(z–z₀)ⁿ⁺¹dz=2πi/n!*w⁽ⁿ⁾(z₀) – интегральная формула Коши.

a-₁=Res_z=z0 f(z) – вычет функции f(z) в точке z_0.

∫_С f(z)dz=2πi*Res_z=z0 f(z), z₀ – особая точка.

Если z₀ – простой полюс, то Res_z=z0 f(z)=lim_z→z0 (f(z)*(z–z₀)).

Если z₀ – полюс порядка m, то Res_z=z0 f(z)=1.(ь-1)!*lim_z→z0 (f(z)*(z–z₀)^m)^(m-1).

Основная теорема о вычетах: Пусть функция f(z) является аналитической в некоторой области D кроме конечного числа изолированных особых точек (полюсов и существенно особых точек).

z₁, z₂, …, z_n – конечное число изолированных особых точек.

Тогда интеграл по замкнутому контуру с охватывающей эти изолированные точки равен 2πi на сумму вычетов в каждой точке, охватываемой контуром C.

∫_C f(z)dz=2πi ∑_k=1 Res_z→zk f(z)

27. Интегрирование функции комплексного переменного. Вычисление контурных интегралов. Свойства контурных интегралов. Независимость контурного интеграла от пути интегрирования. Неопределенный интеграл, формула Ньютона-Лейбница. Примеры.

Пусть дана функция , непрерывная в некоторой областиD. Рассмотрим в этой области гладкую кривую L. Разобьём кривую на n-частей (z₁…z_n) с участками длиной

Предел от S_n существует, единственен и называется интегралом от f(z) по дуге L

Если функция , тоинтеграл представляет собой сумму криволинейных интегралов по дуге L

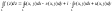
Основные свойства контурных интегралов:

Линейность:

Аддитивность:

Если , причёмточка, то