28. Ряд Тейлора. Единственность разложения аналитической функции в ряд Тейлора

Если f(z) является аналитической в некоторой окрестности точки z₀, то f(z) может быть разложена в ряд Тейлора.

Это разложение единственно. Единственность разложения следует из того, что коэффициенты ряда однозначно выражаются через производные функции.

Ряд Тейлора сходится в круге ,R–радиус круга сходимости.

Если ряд Тейлора задан в виде: , то радиус круга сходимости определяется по одной из формул

29. Ряд Лорана. Единственность разложения аналитической функции в ряд Лорана

Ряд вида:

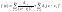
называется рядом Лорана функции f(z). Его часть, содержащая неотрицательные степени , называется правильной, а часть, содержащая отрицательные степени, называется главной.

Правильная часть сходится в круге , а главная сходится вне круга радиусаR₂, т.е

26. Производная функции комплексного переменного. Условие Коши-Римана. Правила дифференцирования. Аналитические функции. Геометрический смысл аргумента и модуля производной.

Производной функции называют предел отношения приращения функции к приращению аргумента

Функция, имеющая производную в точке z_0, называется моногенной в этой точке.

Функция, имеющая производные во всех точках некоторой области, называется аналитической в этой области.

Если , где, то для того, чтобы функция была аналитической необходимо существование частных производных

–условия Коши-Римана

Геометрический смысл аргумента производной функции в точкеz₀ заключается в угле поворота касательной τ при его отображении в плоскость W, т.е аргумент

Геометрический смысл модуля производной имеет смысл искажения масштаба при отображении эллиптического отрезка плоскости z в плоскость W

, k–коэффициент растяжения в точке z₀. Если , то в окрестности точкиz₀ расстояния между точками увеличиваются, если , то сжимаются. Но так как значениене зависит от направления, по которомуz→z₀, то в окрестности z₀ коэффициент растяжения постоянен.

23. Понятие кч. Действия над кч, различные виды кч.

Комплексные числа – числа вида x+iy, где x и y — вещественные числа, i – мнимая единица; то есть i²=–1. Множество всех комплексных чисел обычно обозначается C.

Действия над комплексными числами:

Сравнение: a+bi=c+di означает, что a=c и b=d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

Сложение: (a+bi)+(c+di)=(a+c)+(b+d)i.

Вычитание:(a+bi)–(c+di)=(a–c)+(b–d)i.

Умножение: (a+bi)*(c+di)=ac+bci+adi+bdi²=(ac–bd)+(bc+ad)i.

Деление: (a+bi)/(c+di)=((a+bi)(c-di))/((c+di)(c-di))=(ac+bd)/(c²+d²)+((bc-ad)/(c²+d²))i.

В частности, 1/(a+bi)=a/(a²+b²)–(b/(a²+b²))i.

Виды комплексных чисел:

z=x+iy – алгебраическая фирма;

z=r(cosφ+i*sinφ) – тригонометрическая форма;

z=r*e^iφ – показательная форма