5) Локальная теорема Лапласа

Пользоваться формулой Бернулли при больших значениях  очень трудно. Например, если , то для отыскания вероятности  надо вычислить значение выражения

Естественно, возникает вопрос: нельзя ли вычислить интересующую вероятность, не используя формулу Бернулли? Оказывается, можно. Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления событий ровно  раз в  испытаниях, если число испытаний достаточно велико.

Теорема 3.1. Если вероятность  появления события  в каждом испытании постоянна и отлична от нуля и единицы, то вероятность  того, что событие  появится в  испытаниях ровно  раз, приближенно равна (тем точнее, чем больше ) значению функции

 при .

Существуют таблицы, которые содержат значения функции , соответствующие положительным значениям аргумента . Для отрицательных значений аргумента используют те же таблицы, так как функция  четна, т. е. .

Итак, приближенно вероятность того, что событие  появится в  испытаниях ровно  раз,

 где .

Пример 3. Найти вероятность того, что событие  наступит ровно 80 раз в 400 испытаниях, если вероятность появления события  в каждом испытании равна 0,2.

Решение. По условию . Воспользуемся асимптотической, формулой Лапласа:

Вычислим определяемое данными задачи значение :

По таблице прил, 1 находим . Искомая вероятность

Формула Бернулли приводит примерно к такому же результату (выкладки ввиду их громоздкости опущены):

Интегральная теорема Лапласа

Предположим, что проводится  независимых испытаний, в каждом из которых вероятность появления события  постоянна и равна . Необходимо вычислить вероятность  того, что событие  появится в  испытаниях не менее  и не более  раз (для краткости будем говорить "от  до  раз"). Это можно сделать с помощью интегральной теоремы Лапласа.

Теорема 3.2. Если вероятность  наступления события  в каждом испытании постоянна и отлична от нуля и единицы, то приближенно вероятность  того, что событие  появится в испытаниях от  до  раз,

 где .

При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл  не выражается через элементарные функции. Таблица для интеграла 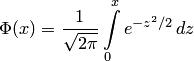 приведена в прил. 2, где даны значения функции  для положительных значений , для  используют ту же таблицу (функция  нечетна, т. е. ). Таблица содержит значения функции  лишь для ; для  можно принять .

Итак, приближенно вероятность того, что событие  появится в  независимых испытаниях от  до  раз,

 где .

Пример 4. Вероятность того, что деталь изготовлена с нарушениями стандартов, . Найти вероятность того, что среди 400 случайно отобранных деталей нестандартных окажется от 70 до 100 деталей.

Решение. По условию . Воспользуемся интегральной теоремой Лапласа:

Вычислим пределы интегрирования:

нижний

верхний

Таким образом

По таблице прил. 2 находим

Искомая вероятность

6)