
- •Лабораторные работы
- •Содержание
- •2 Теоретические сведения по выполняемым
- •Введение
- •Глава 1 обзор виртуальных лабораторий
- •1.1 Star
- •1.2 Ewb
- •1.3 Simulink
- •1.4 Краткие сведения о пакетах Multisim и Mathcad
- •1.4.1 Multisim
- •1.4.2 Mathcad
- •Глава 2 теоретические сведения по выполняемым лабораторным работам
- •2.1 Гармонические осцилляторы
- •2.2 Сложение гармонических колебаний
- •2.3 Ангармонический осциллятор
- •2.4 Параметрические колебания
- •2.5 Нелинейные волны
- •2.6 Хаотические колебания
- •Глава 3 экспериментальная часть
- •3.1 Гармонические осцилляторы
- •3.1.1 Лабораторная работа «Исследование гармонических колебаний»
- •3.1.2 Лабораторная работа «Исследование затухающих гармонических колебаний»
- •3.1.3 Лабораторная работа «Исследование частотных свойств резонансных контуров»
- •3.2 Сложение гармонических колебаний
- •3.2.1 Лабораторная работа «Сложение однонаправленных колебаний»
- •3.2.2 Лабораторная работа «Сложение перпендикулярных колебаний»
- •3.3 Ангармонические осцилляторы
- •3.3.2 Лабораторная работа «Осциллятор Ван-дер-Поля»
- •3.4 Лабораторная работа «Параметрические колебания»
- •3.4.1 Лабораторная работа «Исследование параметрического усилителя»
- •3.5 Лабораторная работа «Нелинейные волны»
- •3.5.1 Лабораторная работа «Солитоны»
- •3.6 Лабораторная работа «Хаотические колебания»
- •3.6.1 Лабораторная работа «Осциллятор Лоренца»
- •3.6.2 Лабораторная работа «Генератор шума»
- •Заключение
- •Литература
2.2 Сложение гармонических колебаний
1. Сложение однонаправленных колебаний.
Сложим два колебания одинаковой частоты, но различных фаз и амплитуд [11].
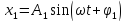 ,
,
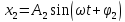 . (2.17)
. (2.17)
При наложении колебаний друг на друга:
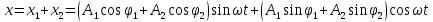 . (2.18)
. (2.18)
Введем
новые параметры
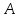 и
и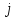 согласно уравнениям:
согласно уравнениям:
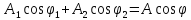 ,
,
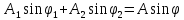 . (2.19)
. (2.19)
Система уравнений (2.19) легко решается:
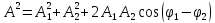 , (2.20)
, (2.20)
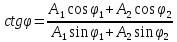 . (2.21)
. (2.21)
Таким
образом, для
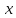 окончательно получаем уравнение:
окончательно получаем уравнение:
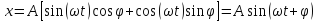 . (2.22)
. (2.22)
Итак, в результате сложения однонаправленных колебаний одинаковой частоты получаем гармоническое (синусоидальное) колебание, амплитуда и фаза которого определяется формулами (2.20) и (2.21).
Рассмотрим частные случаи, при которых соотношения между фазами двух складываемых колебаний различны:
а)
пусть
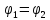 ,
тогда
,
тогда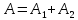 ;
;
б)
пусть
 ,
тогда
,
тогда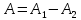 ;
;
в)
пусть
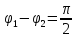 ,
тогда
,
тогда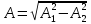 .
.
Сложим теперь однонаправленные колебания одинаковой амплитуды, одинаковых фаз, но разной частоты:
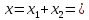
=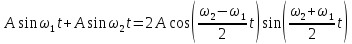 . (2.23)
. (2.23)
Рассмотрим
случай, когда частоты близки друг к
другу, т.е.
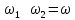 .
Тогда приближенно будем считать, что
.
Тогда приближенно будем считать, что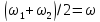 ,
а
,
а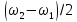 величина малая. Уравнение результирующего
колебания будет иметь вид:
величина малая. Уравнение результирующего
колебания будет иметь вид:
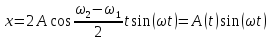 . (2.24)
. (2.24)
Его график изображен на рис. 2.2. Такое колебание называется биением.
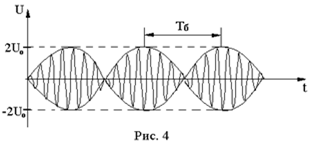
Рис. 2.2 – Биения
Оно
осуществляется с частотой
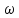 ,
но его амплитуда совершает колебание
с большим периодом.
,
но его амплитуда совершает колебание
с большим периодом.
2. Сложение двух взаимно перпендикулярных колебаний.
Допустим,
что одно колебание осуществляется вдоль
оси
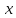 ,
другое – вдоль оси
,
другое – вдоль оси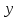 .
Результирующее движение, очевидно,
располагается в плоскости
.
Результирующее движение, очевидно,
располагается в плоскости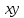 .
.
Допустим, что частоты колебаний и фазы одинаковы, а амплитуды различны.
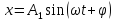 ,
,
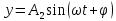 . (2.25)
. (2.25)
Чтобы найти траекторию результирующего движения, нужно из уравнений (2.25) исключить время. Для этого достаточно поделить почленно одно уравнение на другое, в результате получим:
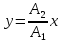 . (2.26)
. (2.26)
Уравнение (2.26) показывает, что в данном случае сложение колебаний приводит к колебанию по прямой линии, тангенс угла наклона которой определяется отношением амплитуд.
Пусть фазы складываемых колебаний отличаются друг от друга на 1/2 и уравнение имеют вид:
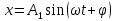 ,
,
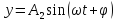 . (2.27)
. (2.27)
Чтобы
найти траекторию результирующего
движения, исключив время, нужно уравнения
(2.27) возвести в квадрат, предварительно
поделив их на
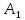 и
и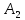 соответственно, а затем сложить. Уравнение
траектории примет вид:
соответственно, а затем сложить. Уравнение
траектории примет вид:
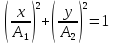 . (2.28)
. (2.28)
Это – уравнение эллипса. Можно доказать, что и при любых начальных фазах и любых амплитудах двух складываемых взаимно перпендикулярных колебаний одинаковой частоты результирующее колебание будет осуществляться по эллипсу. Его ориентация будет зависеть от фаз и амплитуд складываемых колебаний.
Если
же складываемые колебания имеют различные
частоты, то траектории результирующих
движений получаются весьма разнообразными.
Только в случае если частоты колебаний
по
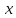 и по
и по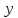 кратны друг другу, получаются замкнутые
траектории. Такие движения можно отнести
к числу периодических. В этом случае
траектории движений называются фигурами
Лиссажу. Рассмотрим одну из фигур
Лиссажу, которая получается при сложении
колебаний с отношениями частот 1:2, с
одинаковыми амплитудами и фазами в
начале движения:
кратны друг другу, получаются замкнутые
траектории. Такие движения можно отнести
к числу периодических. В этом случае
траектории движений называются фигурами
Лиссажу. Рассмотрим одну из фигур
Лиссажу, которая получается при сложении
колебаний с отношениями частот 1:2, с
одинаковыми амплитудами и фазами в
начале движения:
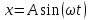 ;
;
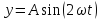 . (2.29)
. (2.29)
Вдоль
оси у колебания происходят в два раза
чаще, чем вдоль оси
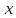 .
Сложение таких колебаний приведет к
траектории движения в виде восьмерки
(рис. 2.3).
.
Сложение таких колебаний приведет к
траектории движения в виде восьмерки
(рис. 2.3).
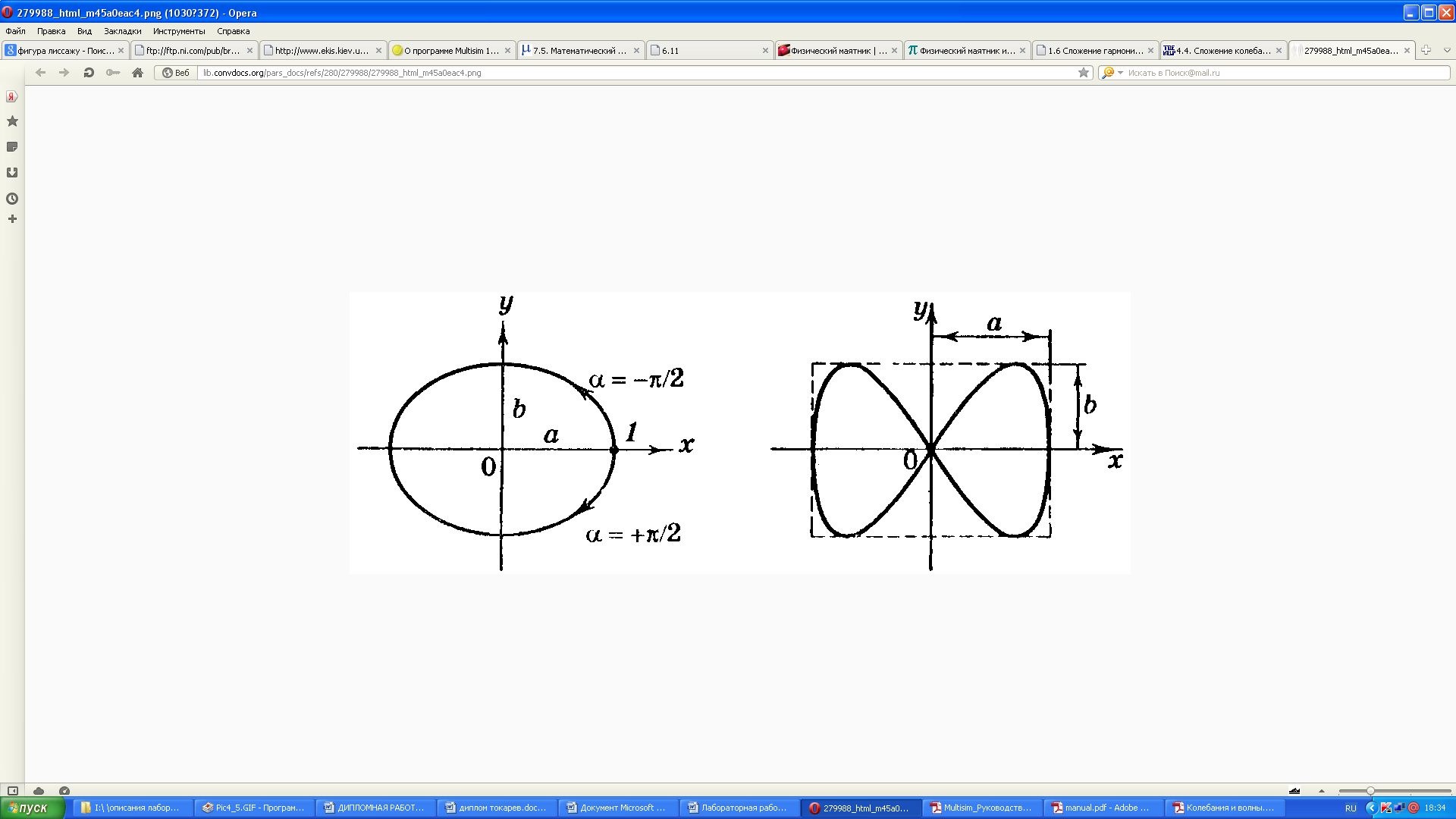
Рис. 2.3 – Фигура Лиссажу
