
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
1. Варианты контрольных заданий по дифференциальному исчислению.
Вариант 1
1. Вычислить пределы с помощью правила Лопиталя:
а)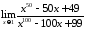 ;
б)
;
б)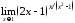
2.
Провести исследование и построить
график функции:
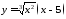 .
.
3.
Построить график функции в полярной
системе координат
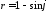 .
.
4.
Найти стороны
 и
и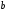 прямоугольника, вписанного в окружность
единичного
прямоугольника, вписанного в окружность
единичного
радиуса и имеющего среди всех таких прямоугольников наибольшую площадь.
5.
Вычислить
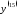 функции
функции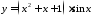 .
.
6.
Используя формулу Тейлора 2 - го порядка,
вычислить приближенно
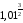 и
и
доказать, что при
этом погрешность
 допускает нижеследующую оценку:
допускает нижеследующую оценку:
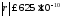
7.
Составить уравнения касательной и
нормали к кривой
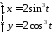 в точке
в точке
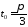 и вычислить
и вычислить
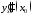 .
.
8.
Вычислить производную 2-го порядка от
неявной функции:
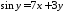 .
.
9.
Вычислить предел с помощью формулы
Тейлора:
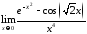 .
.
10.
Известно, что
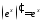 для всех
для всех .
Существуют ли еще какие-нибудь
.
Существуют ли еще какие-нибудь
функции, совпадающие со своими производными всюду?
11. По графику функции построить график ее первой производной
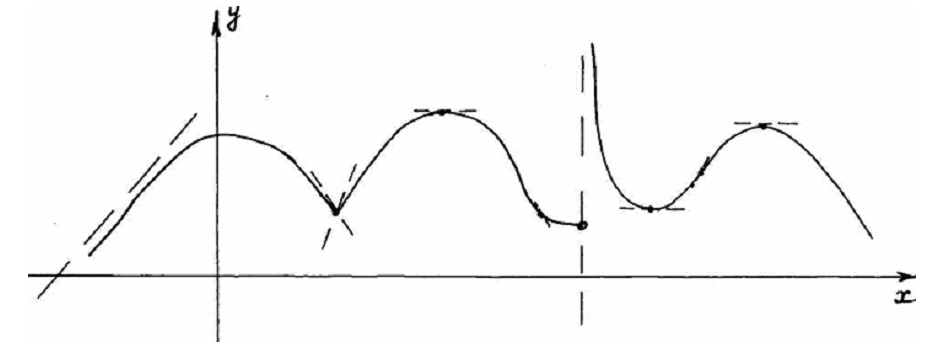
Вариант 2
1. Вычислить пределы с помощью правила Лопиталя:
а)
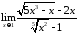 ;
б)
;
б)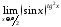 .
.
2.
Провести исследование и построить
график функции:
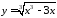 .
.
3.
Построить график функции в полярной
системе координат
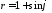 .
.
4.
В трапеции три стороны имеют длину
 .
Какую длину должна иметь четвертая
.
Какую длину должна иметь четвертая
сторона, чтобы площадь была максимальной?
5.
Вычислить
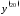 функции
функции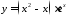 .
.
6.
Используя формулу Тейлора
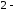 го
порядка, вычислить приближенно значение
го
порядка, вычислить приближенно значение
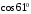 и
доказать, что при этом погрешность
и
доказать, что при этом погрешность
 допускает
нижеследующую
допускает
нижеследующую
оценку:
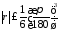 .
.
7.
Составить уравнения касательной и
нормали к кривой
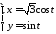 в точке
в точке
 и вычислить
и вычислить
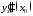 .
.
8.
Вычислить производную 2-го порядка от
неявной функции:
 .
.
9.
Вычислить предел с помощью формулы
Тейлора:
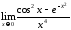 .
.
10.
В формуле Лагранжа определить значение
 для функции
для функции
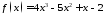 на отрезке
на отрезке
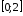 .
.
11. По графику функции построить график ее первой производной
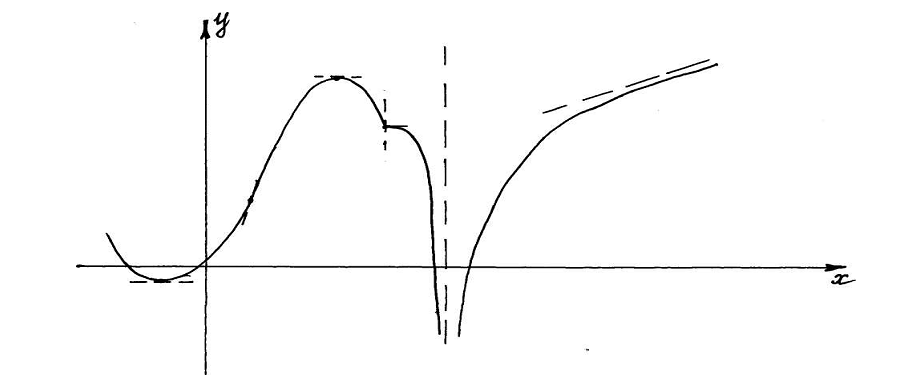
Вариант 3
1. Вычислить пределы с помощью правила Лопиталя:
а)
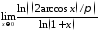 ;
б)
;
б)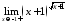 .
.
2.
Провести исследование и построить
график функции:
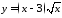 .
.
3.
Построить график функции в полярной
системе координат
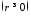
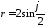 .
.
4.
Найти радиус основания
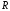 и образующую
и образующую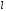 прямого кругового конуса,
прямого кругового конуса,
вписанного в сферу единичного радиуса и имеющего среди таких конусов
наибольшую полную поверхность.
5.
Вычислить
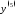 функции
функции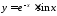 .
.
6.
Используя формулу Тейлора
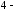 го
порядка, вычислить приближенно значение
го
порядка, вычислить приближенно значение
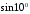 и
доказать, что при этом погрешность
и
доказать, что при этом погрешность
 допускает нижеследующую
допускает нижеследующую
оценку:
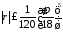 .
.
7.
Составить уравнения касательной и
нормали к кривой
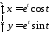 в точке
в точке
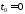 и вычислить
и вычислить
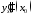 .
.
8.
Вычислить производную 2-го порядка от
неявной функции:
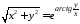 .
.
9.
Вычислить предел с помощью формулы
Тейлора:
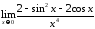 .
.
10.
Применима ли теорема Ролля к функции
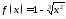 на отрезке
на отрезке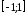 ?
?
11. По графику функции построить график ее первой производной
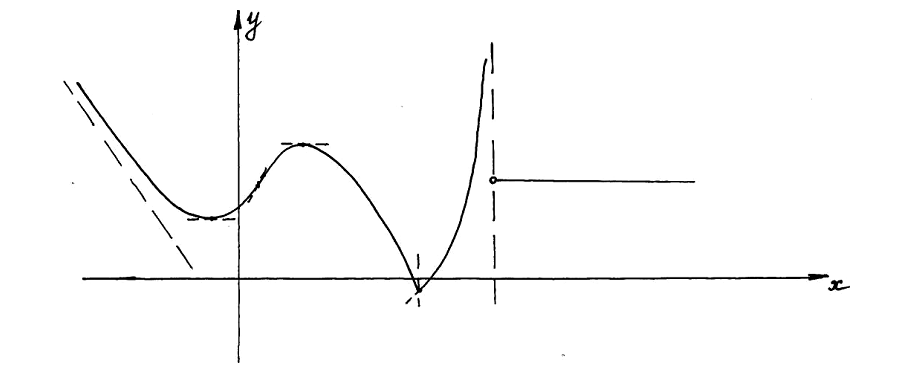
Вариант 4
1. Вычислить пределы с помощью правила Лопиталя:
а)
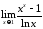 ;
б)
;
б)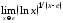 .
.
2.
Провести исследование и построить
график функции:
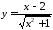
3.
Построить график функции в полярной
системе координат
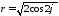 .
.
4.
Найти радиус основания
 и образующую
и образующую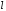 прямого кругового конуса,
прямого кругового конуса,
вписанного в сферу единичного радиуса и имеющего среди таких конусов
наибольший объем.
5.
Вычислить
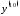 функции
функции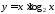 .
.
6.
Используя формулу Тейлора
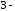 го
порядка, вычислить приближенно
го
порядка, вычислить приближенно
значение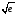 и
доказать, что при этом погрешность
и
доказать, что при этом погрешность допускает
допускает
нижеследующую
оценку:
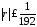 .
.
7.
Составить уравнения касательной и
нормали к кривой
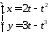 в точке
в точке
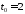 и вычислить
и вычислить
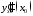 .
.
8.
Вычислить производную 2-го порядка от
неявной функции:
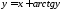 .
.
9.
Вычислить предел с помощью формулы
Тейлора:
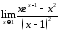 .
.
10.
Написать формулу Лагранжа для функции
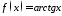 и найти
и найти на
на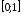 .
.
11. По графику функции построить график ее первой производной

