
Курсовая №4 от 12.02.2012г
.docВариант 1
1.Расставить пределы интегрирования двумя способами в двойном интеграле
![]() в
декартовых координатах для области
в
декартовых координатах для области
![]()
![]() :
:
![]() ;
;
![]() .
.
2.
Вычислить двойной интеграл:
![]() ;
;
![]() :
:
![]() ,
,
![]() .
.
3.
Вычислить двойной интеграл:
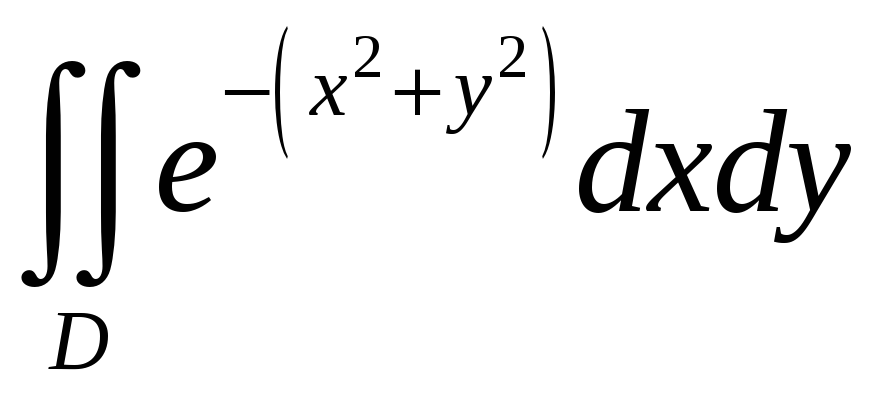 ;
;
![]() :
:
![]() .
.
4.
Вычислить тройной интеграл:
![]() ;
;
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
5.
Найти площадь области, ограниченной
кривыми:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
6.
Найти объем тела, ограниченного
поверхностями:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() и параболоидом
и параболоидом
![]() .
.
7.
Вычислить:![]() ,
где
,
где
![]() окружность
окружность
![]() .
.
8.
Вычислить непосредственно и с помощью
формулы Грина:
![]() ,
где
,
где
![]() контур
треугольника
контур
треугольника
![]()
![]() ,
,
![]() ,
,
![]() .
.
9.
Проверить, является ли данное выражение
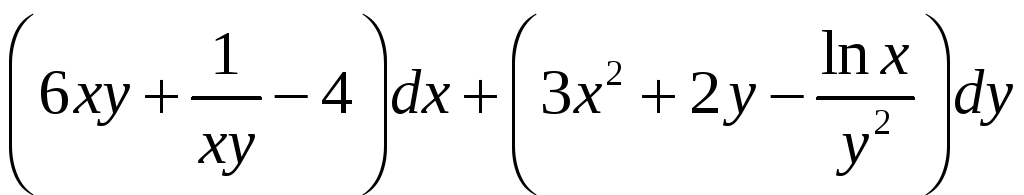 полным дифференциалом. Если да, то найти
полным дифференциалом. Если да, то найти
![]() .
.
10.
Вычислите поток векторного поля
![]() через
через
внешнюю сторону
границы области, ограниченной поверхностями
![]() ,
,
![]() ,
,
![]() и
и
![]() .
.
11.
Найдите циркуляцию векторного поля
![]() по ломаной
по ломаной
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
При вычислении
.
При вычислении
по теореме Стокса в качестве поверхности, опирающейся на контур, выберите
поверхность,
образованную гранями
![]() и
и
![]() пирамиды
пирамиды
![]() .
.
12.
Найти дивергенцию и ротор векторного
поля
![]() ;
выяснить, является ли данное
;
выяснить, является ли данное
поле потенциальным или соленоидальным; если да, то найти соответственно
его скалярный или векторный потенциал и сделать проверку потенциала:
![]()
Вариант 2
1.Расставить пределы интегрирования двумя способами в двойном интеграле
![]() в декартовых
координатах для области
в декартовых
координатах для области
![]()
![]()
![]()
![]()
![]()
2.
Вычислить двойной интеграл:![]()
![]()
![]()
![]()
![]()
![]()
3.
Вычислить двойной интеграл:
![]() ;
;
![]()
![]()
![]()
4. Вычислить тройной интеграл:
![]() ;
;
![]()
![]()
![]()
![]()
![]()
5.
Найти площадь области, ограниченной
кривыми:![]()
![]()
6.
Найти объем тела, ограниченного
поверхностями:
![]() ,
,
![]() и цилиндром
и цилиндром
![]() .
.
7.
Вычислить:
![]() ,
где
,
где
![]() контур прямоугольника
контур прямоугольника
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
8. Вычислить непосредственно и с помощью формулы Грина:
![]() ,
где
,
где
![]() окружность
окружность
![]() .
.
9.
Проверить, является ли данное выражение
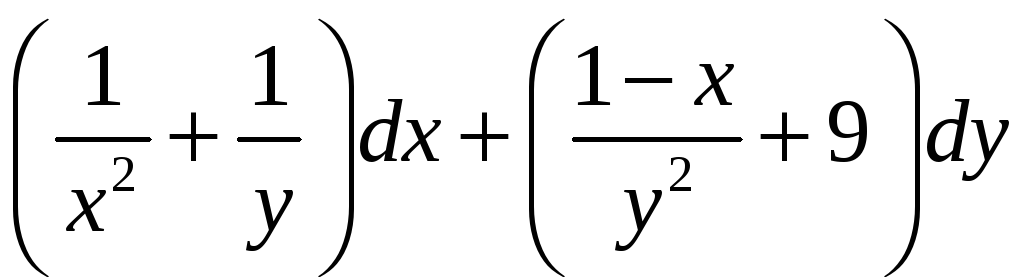 полным дифференциалом. Если да, то найти
полным дифференциалом. Если да, то найти
![]() .
.
10.
Вычислите поток векторного поля
![]() через внешнюю
через внешнюю
сторону границы
области, ограниченной поверхностями
![]() и
и
![]() .
.
11.
Вычислить криволинейный интеграл
(циркуляцию)
![]() ,
где
,
где
![]() линия пересечения цилиндра
линия пересечения цилиндра
![]() с плоскостью
с плоскостью
![]() .
.
12.
Найти дивергенцию и ротор векторного
поля
![]() ;
выяснить, является ли данное
;
выяснить, является ли данное
поле потенциальным или соленоидальным; если да, то найти соответственно
его скалярный или векторный потенциал и сделать проверку потенциала:
![]()
Вариант 3
1.Расставить пределы интегрирования двумя способами в двойном интеграле
![]() в декартовых
координатах для области
в декартовых
координатах для области
![]()
![]()
![]()
![]()
2.
Вычислить двойной интеграл:
![]() ;
;
![]()
![]()
![]()
![]()
![]() .
.
3.
Вычислить двойной интеграл:
![]()
![]()
![]()
![]()
4.
Вычислить тройной интеграл:
![]()
![]()
![]()
![]()
5.
Найти площадь области, ограниченной
кривыми:![]()
![]()
6.
Найти объем тела, ограниченного
поверхностями:
![]() и параболоидом
и параболоидом
![]() .
.
7.
Вычислить:
![]() ,
где
,
где
![]() первая
арка циклоиды
первая
арка циклоиды
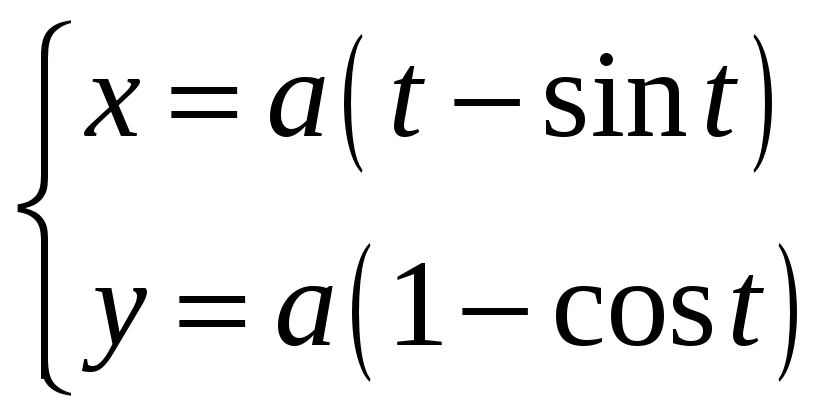 .
.
8.
Вычислить непосредственно и с помощью
формулы Грина:
![]() ,
где
,
где
![]() часть
параболы
часть
параболы
![]() и хорда, проходящая через точки
и хорда, проходящая через точки
![]() ,
,
![]() .
.
9.
Проверить, является ли данное выражение
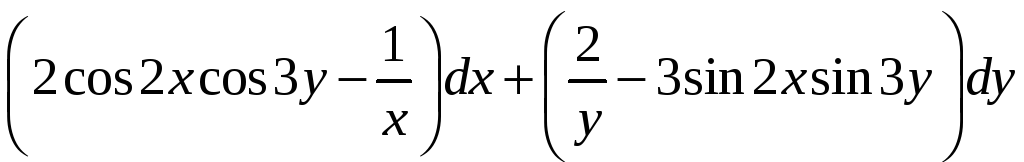 полным дифференциалом. Если да, то найти
полным дифференциалом. Если да, то найти
![]() .
.
10.
Вычислите поток векторного поля
![]() через внешнюю сторону
через внешнюю сторону
границы области,
ограниченной поверхностями
![]() ,
,
![]() ,
,
![]() и
и
![]() .
.
11.
Найдите циркуляцию векторного поля
![]() по контуру,
по контуру,
образованному
пересечением параболоида
![]() с плоскостями
с плоскостями
![]() ,
,![]() ,
,
![]()
![]() .
.
12.
Найти дивергенцию и ротор векторного
поля
![]() ;
выяснить, является ли данное поле
потенциальным или соленоидальным; если
да, то найти соответственно его скалярный
или векторный потенциал и сделать
проверку потенциала:
;
выяснить, является ли данное поле
потенциальным или соленоидальным; если
да, то найти соответственно его скалярный
или векторный потенциал и сделать
проверку потенциала:
![]()
Вариант 4
1.Расставить пределы интегрирования двумя способами в двойном интеграле
![]() в декартовых
координатах для области
в декартовых
координатах для области
![]()
![]()
![]()
![]()
2.
Вычислить двойной интеграл:
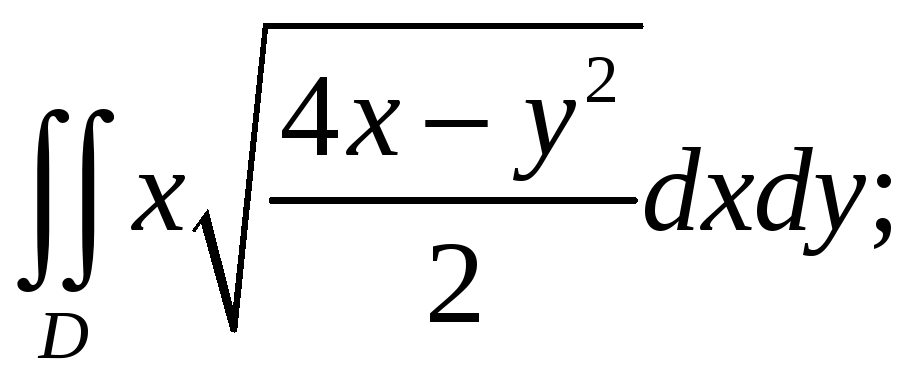
![]()
![]()
![]()
![]()
3.
Вычислить двойной интеграл:
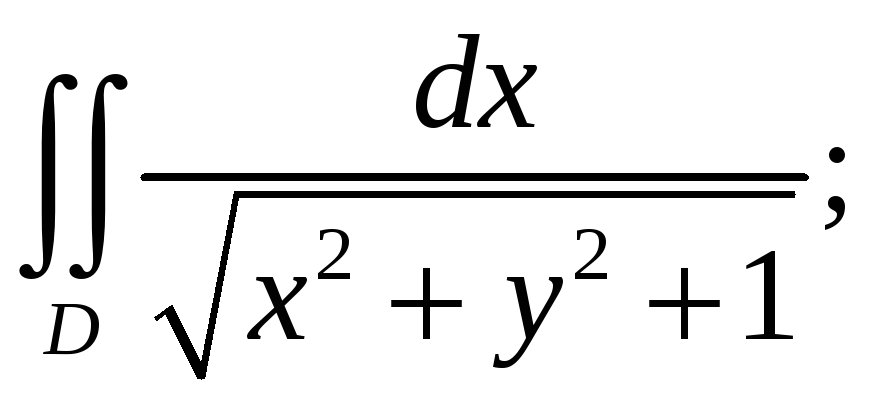
![]()
![]()
![]()
4.
Вычислить тройной интеграл:
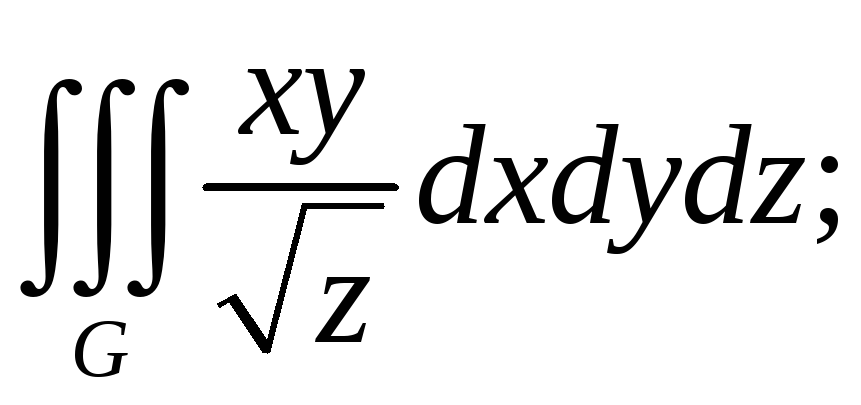
![]()
![]()
![]()
![]()
![]()
![]()
5.
Найти площадь области, ограниченной
кривыми:![]()
![]()
6.
Найти объем тела, ограниченного
поверхностями:
![]() ,
,
![]() ,
,
![]() ,
,
гиперболическим
параболоидом
![]() и цилиндром
и цилиндром
![]() .
.
7.
Вычислить:
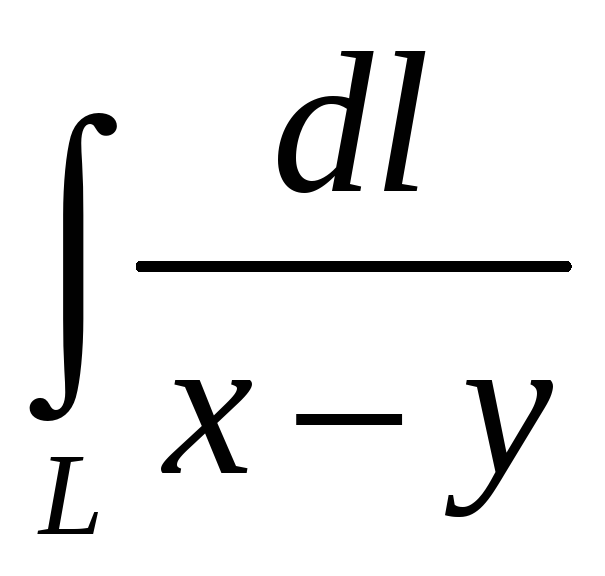 ,
где
,
где
![]() отрезок
прямой
отрезок
прямой
![]() ,
соединяющая точки
,
соединяющая точки
![]() и
и
![]() .
.
8. Вычислить непосредственно и с помощью формулы Грина:
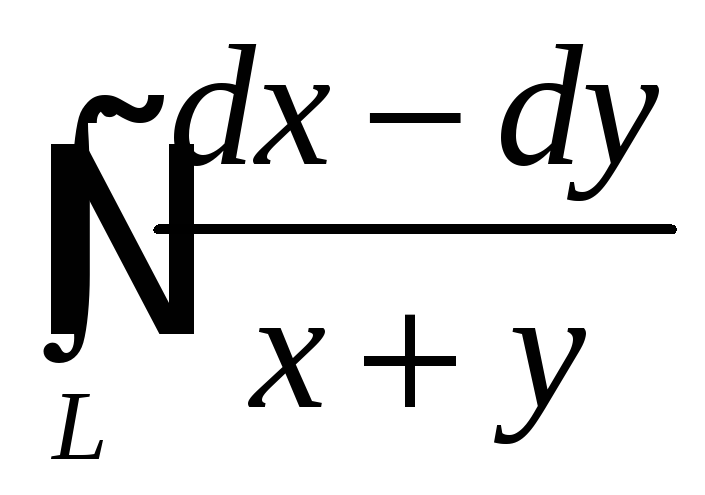 ,
где
,
где
![]() квадрат
квадрат
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
9.
Проверить, является ли данное выражение
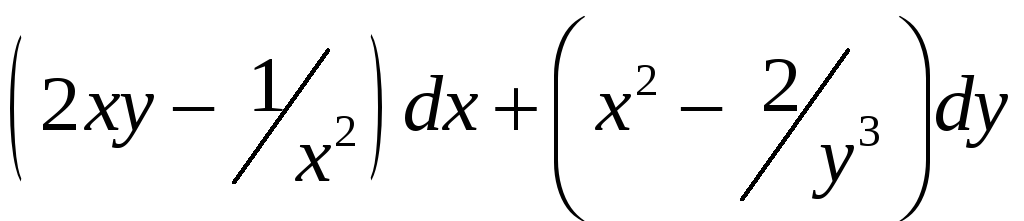 полным дифференциалом. Если да, то найти
полным дифференциалом. Если да, то найти
![]() .
.
10.
Вычислите поток векторного поля
![]() через внешнюю сторону границы области,
ограниченной поверхностями
через внешнюю сторону границы области,
ограниченной поверхностями
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() и
и
![]() .
.
11.
Вычислить криволинейный интеграл
(циркуляцию)
![]() ,
где
,
где
![]() линия пересечения цилиндра
линия пересечения цилиндра
![]() с плоскостью
с плоскостью
![]() .
.
12.
Найти дивергенцию и ротор векторного
поля
![]() ;
выяснить, является ли данное
;
выяснить, является ли данное
поле потенциальным или соленоидальным; если да, то найти соответственно
его скалярный или векторный потенциал и сделать проверку потенциала:
![]()
Вариант 5
1.Расставить пределы интегрирования двумя способами в двойном интеграле
![]() в декартовых
координатах для области
в декартовых
координатах для области
![]()
![]()
![]()
![]()
2.
Вычислить двойной интеграл:
![]()
![]()
![]()
![]()
![]()
3.
Вычислить двойной интеграл:
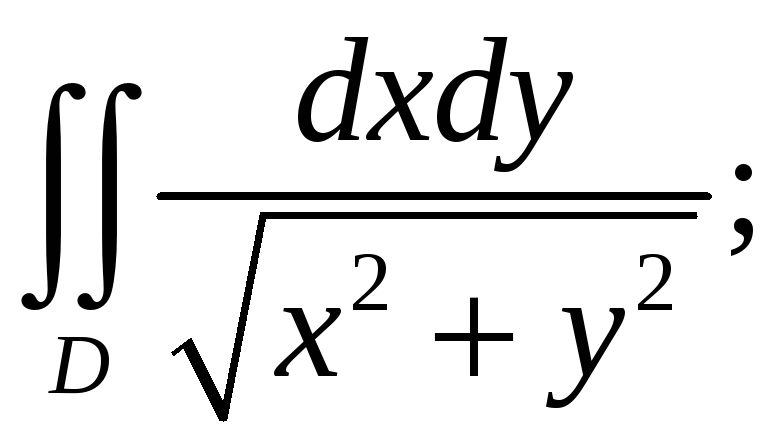
![]()
![]()
![]() ,
,![]()
4.
Вычислить тройной интеграл:
![]()
![]()
![]()
![]()
5.
Найти площадь области, ограниченной
кривыми:![]()
![]()
![]()
![]()
6.
Найти объем тела, ограниченного
поверхностями: эллиптическим параболоидом
![]() ,
плоскостью
,
плоскостью
![]() и
и
![]() ,
,
![]() ,
,
![]() .
.
7.
Вычислить:
![]() ,
где
,
где
![]() часть эллипса
часть эллипса
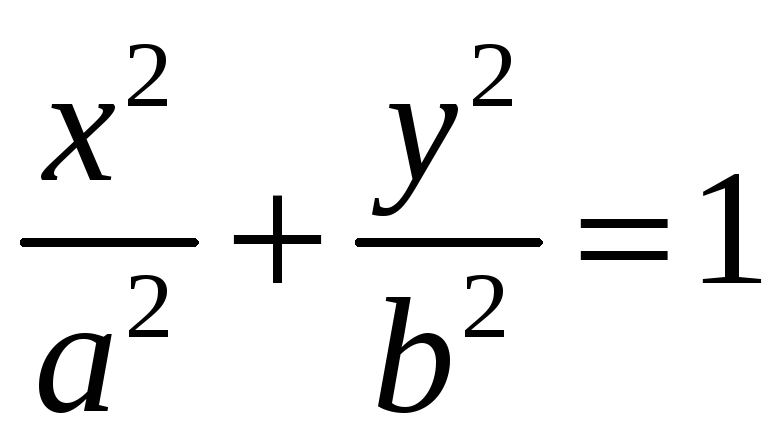 ,
лежащая в
,
лежащая в
![]() четверти.
четверти.
8.
Вычислить непосредственно и с помощью
формулы Грина:
![]() ,
где
,
где
![]() окружность
окружность
![]() .
.
9.
Проверить, является ли данное выражение
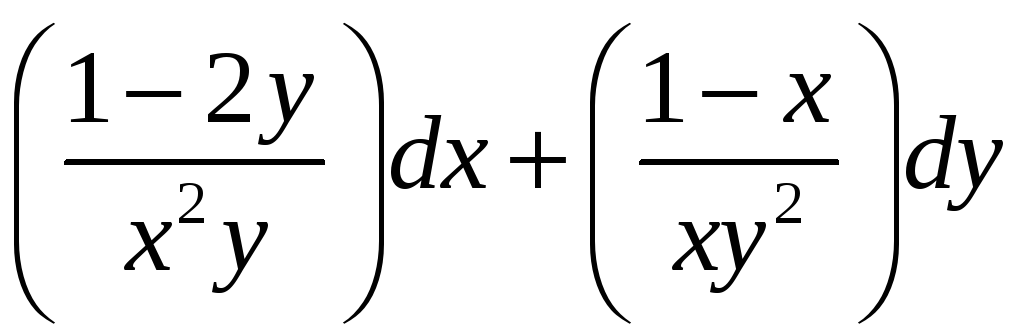 полным дифференциалом. Если да, то найти
полным дифференциалом. Если да, то найти
![]() .
.
10.
Вычислите поток векторного поля
![]() через внешнюю сторону границы области,
ограниченной поверхностями
через внешнюю сторону границы области,
ограниченной поверхностями
![]() ,
,
![]() ,
,
![]() и
и
![]() .
.
11.
Найдите циркуляцию векторного поля
![]() вдоль эллипса, образованного
пересечением гиперболоида
вдоль эллипса, образованного
пересечением гиперболоида
![]() с плоскостью
с плоскостью
![]() .
.
12.
Найти дивергенцию и ротор векторного
поля
![]() ;
выяснить, является ли данное поле
потенциальным или соленоидальным; если
да, то найти соответственно его скалярный
или векторный потенциал и сделать
проверку потенциала:
;
выяснить, является ли данное поле
потенциальным или соленоидальным; если
да, то найти соответственно его скалярный
или векторный потенциал и сделать
проверку потенциала:
![]()
Вариант 6
1.Расставить пределы интегрирования двумя способами в двойном интеграле
![]() в декартовых
координатах для области
в декартовых
координатах для области
![]()
![]()
![]()
![]()
2.
Вычислить двойной интеграл:
![]()
![]()
![]()
![]()
![]()
![]()
3.
Вычислить двойной интеграл:
![]()
![]()
![]()
![]()
4.
Вычислить тройной интеграл:
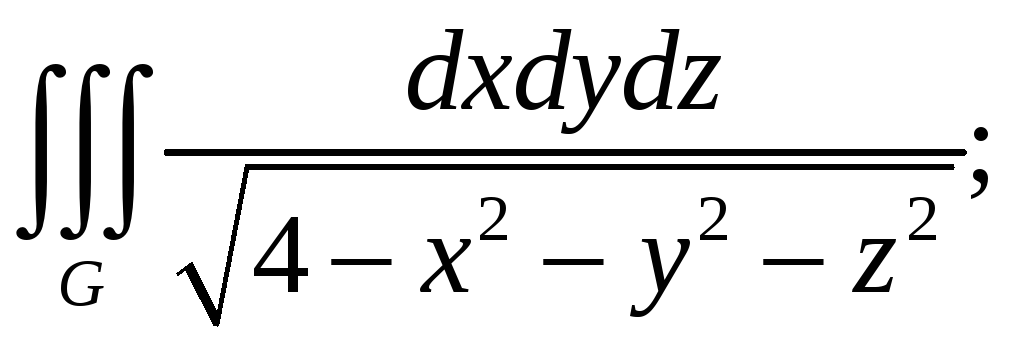
![]()
![]()
![]()
![]()
![]() .
.
5.
Найти площадь области, ограниченной
кривыми:![]()
![]()
6.
Найти объем тела, ограниченного
поверхностями: цилиндром
![]() и плоскостями
и плоскостями
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
7.
Вычислить:
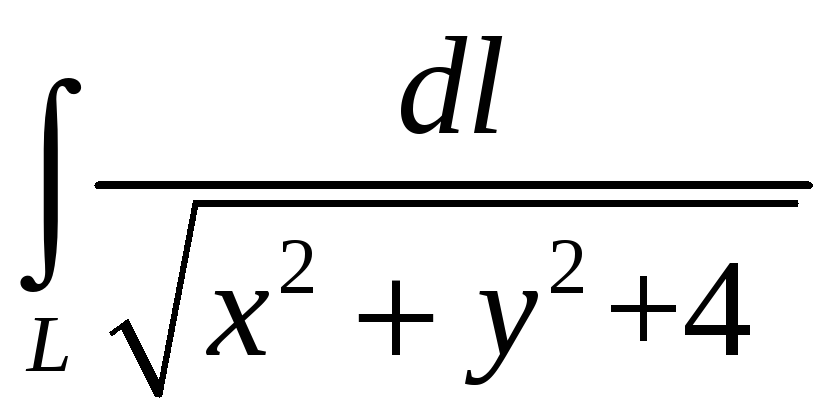 ,
где
,
где
![]() прямая,
соединяющая точки
прямая,
соединяющая точки
![]() и
и
![]() .
.
8.
Вычислить непосредственно и с помощью
формулы Грина:
![]() ,
где
,
где
![]() эллипс
эллипс
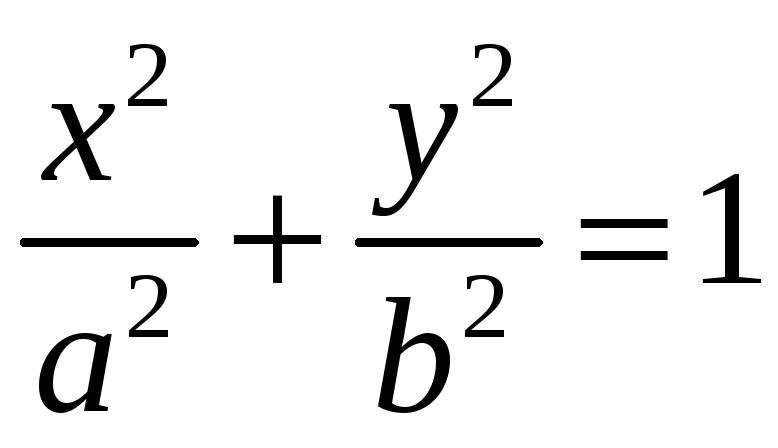 .
.
9.
Проверить, является ли данное выражение
![]() полным дифференциалом. Если да, то найти
полным дифференциалом. Если да, то найти
![]() .
.
10.
Вычислите поток векторного поля
![]() через внешнюю сторону границы области,
ограниченной поверхностями
через внешнюю сторону границы области,
ограниченной поверхностями
![]() ,
,
![]() ,
и
,
и
![]() (
(![]() ).
).
11.
Вычислить криволинейный интеграл
(циркуляцию)
![]() ,
где
,
где
![]() линия пересечения цилиндра
линия пересечения цилиндра
![]() с плоскостью
с плоскостью
![]() .
.
12.
Найти дивергенцию и ротор векторного
поля
![]() ;
выяснить, является ли данное поле
потенциальным или соленоидальным; если
да, то найти соответственно его скалярный
или векторный потенциал и сделать
проверку потенциала:
;
выяснить, является ли данное поле
потенциальным или соленоидальным; если
да, то найти соответственно его скалярный
или векторный потенциал и сделать
проверку потенциала:
![]()
Вариант 7
1.Расставить пределы интегрирования двумя способами в двойном интеграле
![]() в декартовых
координатах для области
в декартовых
координатах для области
![]()
![]()
![]()
![]()
2.
Вычислить двойной интеграл:
![]()
![]()
![]()
![]()
3.
Вычислить двойной интеграл:
![]()
![]()
![]()
