
Логика_РГР
.pdfПОВОЛЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
ЛОГИЧЕСКИЕ ОСНОВЫ ЭВМ
Методические указания к выполнению расчетно-графической работы для студентов радиотехнического факультета
Йошкар-Ола
2012
2
УДК: 681.3
Логические основы ЭВМ: Методические указания к выполнению расчетно-графической работы для студентов радиотехнического факультета / Сост. Т.А. Лежнина. – Йошкар-
Ола: ПГТУ, 2012. – 28 с.
Приведены теоретические сведения по разделу информатики – логическим основам вычислительной техники. Материал содержит описание основных логических функций и их реализаций в виде логических элементов. Рассмотрены основные законы алгебры логики и их применение для преобразования логических функций. Приведены варианты заданий по РГР.
Для студентов очной формы обучения, выполняющих РГР, и студентов заочной формы обучения, выполняющих контрольную работу по дисциплине « Информатика».
© ПГТУ, 2012
3
ВВЕДЕНИЕ
В рамках темы «Логические основы ЭВМ» рассматриваются основные понятия математической логики, необходимые при изучении базового курса информатики, а также их использование в схемотехническом аспекте.
Знание логических операций и умение строить логические выражения позволяют:
-легко и быстро освоить выражения и условные операторы любого языка программирования процедурного типа;
-эффективно использовать логические выражения и логические величины при работе с электронными таблицами и базами данных;
-ознакомиться с логическими схемами компонентов компьютера: вентилей, сумматоров, триггеров, предназначенных для обработки и хранения двоичной информации.
1. ЛОГИКА ВЫСКАЗЫВАНИЙ. ЭЛЕМЕНТАРНЫЕ ЛОГИЧЕСКИЕ ФУНКЦИИ
1.1. Основные понятия математической логики
Логика - это наука, изучающая методы установления истинности или ложности одних высказываний на основе истинности или ложности других высказываний. Основы логики как науки были заложены в IV в. до н.э. древнегреческим ученым Аристотелем. Правила вывода истинности высказываний, описанные Аристотелем (силлогизмы) оставались основным инструментом логики вплоть до второй половины XIX в., когда в трудах Дж.Буля, О. де Моргана и др. возникла математическая логика (алгебра логики), которая в отличие от обычной алгебры оперирует не числами, а высказываниями.
Высказывание - это любое утверждение, относительно которого можно сказать истинно оно или ложно, т.е. соответствует оно действительности или нет. Например, «треугольник – это геометрическая фигура» – истинное высказывание, а «1=2» – это ложное высказывание. Следовательно, истинность высказываний выражается через логические величины ИСТИНА (true) или ЛОЖЬ (false). Таким образом, по своей сути высказывания фактически являются двоичными объектами и поэтому часто
4
истинному значению высказывания ставят в соответствие 1, а ложному - 0. Например, запись А = 1 означает, что высказывание А истинно.
Логические переменные могут принимать значения только ИСТИНА или ЛОЖЬ. Логическое выражение – это простое или сложное высказывание. Сложное высказывание строится из простых с помощью
логических операций (связок).
В алгебре логики определены пять основных логических операций: конъюнкция, дизъюнкция, отрицание, импликация, эквивалентность. Первые три из них составляют полную систему операций, вследствие чего остальные операции могут быть выражены через них (нормализованы).
Логические связки, а также названия соответствующих им логических операций и обозначений приведены в таблице 1 [1].
|
|
Таблица 1 |
|
|
|
Логическая связка |
Названия логической операции |
Обозначения |
|
|
|
не |
Отрицание, инверсия |
– , ` , Ø |
|
|
|
и, а, но, хотя |
Конъюнкция, логическое |
&, × , Ù |
|
умножение, логическое И |
|
|
|
|
или |
Дизъюнкция, нестрогая |
Ú , + |
|
дизъюнкция, логическое сложение, |
|
|
логическое ИЛИ |
|
либо |
Разделительная (строгая) |
Å, D |
|
дизъюнкция, исключающее ИЛИ, |
|
|
сложение по модулю 2 |
|
если …, то |
Импликация, следование |
, ® |
тогда и только тогда, |
Эквивалентность, равнозначность |
Û , « , º , ~ |
когда |
|
|
|
|
|
|
|
|
1.2. Схемотехнический аспект математической логики
ЭВМ строятся из компонентов с двумя устойчивыми состояниями. Одно состояние обозначается нулем, другое – единицей. Под воздействием двоичных сигналов компоненты изменяют свои состояния. Очевидно, что компоненты ЭВМ, выполняющие арифметические и логические операции, можно рассматривать как преобразователи двоичной информации, а их
5
функционирование описывать логическими функциями. По этой причине алгебра логики находит непосредственное и широкое применение при разработке и использовании средств электронной вычислительной техники.
Дискретный преобразователь, который выдает после обработки двоичных сигналов значение одной из логических операций, называется
логическим элементом (вентилем).
Логические функции и, соответственно, работа логических элементов описываются так называемыми таблицами истинности. Таблица истинности – это таблица, устанавливающая соответствие между возможными наборами значений логических переменных (входных сигналов) и значениями функций (выходных сигналов).
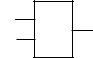
Для иллюстрации сказанного рассмотрим логический элемент (ЛЭ), представленный на рис. 1а.
x1 ЛЭ
F
x2
x1 |
x2 |
F |
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
|
|
а) б)
Рис. 1. Пример логического элемента и его таблицы истинности
На элемент воздействуют два входных двоичных сигнала, описываемые логическими переменными х1 и х2. Выходной сигнал F как функция
F= f (x1 , x2 ) принимает единичное значение при единичных значениях х1
их2 (х1=1, х2=1).
Во всех остальных случаях выходной сигнал принимает нулевое значение. Такому словесному описанию функционирования ЛЭ соответствует таблица истинности, представленная на рис. 1б. Возможным наборам значений логических переменных х1, х2 (00, 01, 10, 11) соответствуют десятичные цифры 0, 1, 2 и 3. Поэтому можно считать, что функция F принимает единичное значение на наборе 3. Количество возможных наборов переменных зависит от числа этих переменных. Если функция Z зависит от одной переменной, т. е. Z = f (x) , то всего наборов

|
|
6 |
значений х |
два (х=0, х=1). Для рассмотренной ранее функции |
|
F = f (x , x |
2 |
) , которая зависит от двух переменных, возможных наборов |
1 |
|
|
значений переменных четыре: 00, 01, 10, 11. Для некоторой логической функции от трех переменных Q = f (x1 , x2 , x3 ) возможных наборов
будет восемь: 000, 001, 010, 011,..., 111. Очевидно, что в общем случае количество N возможных наборов значений переменных логической
функции можно определить по формуле N = 2r , где r – количество переменных, от которых зависит логическая функция.
Сложные логические функции, как правило, выражаются через простые логические функции. Простые логические функции, зависящие от одной или двух логических переменных, называются элементарными. Далее логические переменные будут называться переменными.
1.3. Элементарные логические функции
Логическое отрицание (инверсия)
Отрицание – это логическая функция от одной переменной, которая принимает единичное значение при нулевом значении переменной и
наоборот. Возможные обозначения инверсии: ¬х; x; NOTx .
Таблица истинности этой функции представлена на рис. 2а. Функция логического отрицания описывает функционирование логического элемента «НЕ» (инвертора), условно– графическое обозначение которого приведено на рис. 2б [2]. Единичный сигнал на выходе инвертора появляется при нулевом сигнале на входе (x=0, F=1), и наоборот, нулевой сигнал на выходе появляется при единичном сигнале на входе (x=1, F=0).
x |
|
F |
|
|
|
|
|
|
x |
|
1 |
|
|
||
|
|
|
|
|
|
||
0 |
|
1 |
|
|
|
F |
|
|
|
|
|
||||
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
б) |
|||
Рис. 2. Элемент «НЕ»
7
Логическое умножение (конъюнкция)
Логическое умножение – это логическая функция, по крайней мере, от двух переменных, которая принимает единичное значение при единичных значениях всех переменных. Функция логического умножения называется также конъюнкцией. Возможные обозначения конъюнкции:
х1 И х2; х1 х2; х1&х2; х1·х2; х1 AND х2; х1х2 .
Элементарная конъюнкция зависит от двух переменных. Конъюнкция характеризуется таблицей истинности, представленной на рис. 3а, и описывает работу логического элемента (вентиля) «И» (рис. 3б). Единичный сигнал появляется на выходе этого элемента только при наличии единичного сигнала и на входе х1, и на входе х2.
В общем случае элемент «И» может иметь n входов (рис. 3в). При этом он реализует конъюнкцию от n переменных, т.е.
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
x1 |
x2 |
F |
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
0 |
0 |
|
x1 |
|
|
& |
|
F |
. |
|
|
F |
||
|
|
|
|
|
|||||||||||
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||
|
x2 |
|
|
|
. |
|
|
|
|||||||
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
. |
|
|
|
|||||
1 |
1 |
1 |
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
б) |
|
|
|
|
|
в) |
||
Рис. 3. Элемент «И»
Функция Шеффера
Это логическая функция, по крайней мере, от двух переменных, которая принимает нулевое значение при единичных значениях всех переменных. Таблица истинности функции представлена на рис. 4а. Эта функция читается как «x1 штрих Шеффера x2». Эта функция называется также функцией отрицания конъюнкции. Функция принимает единичные значения на наборах 0, 1, 2 и нулевое значение – только на наборе 3, т. е. тогда, когда обе переменные равны единице. Запись функции:
F = x1 |
|
x2 ; |
F = |
x1 × x2 |
|
F = |
|
; |
F = |
|
. |
|
; |
x1 x2 |
x1 x2 |

8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
x1 |
x2 |
|
F |
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
0 |
0 |
|
1 |
|
|
x1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
. |
|
|
F |
||||||||
|
|
|
|
|
|
|
|
|||||||||||
0 |
1 |
|
1 |
|
|
|
|
|
|
|
|
F |
|
|
||||
|
|
|
x2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
xn |
. |
|
|
|
|
1 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
б) |
|
|
|
|
в) |
|||
|
|
|
|
|
Рис. 4. Элемент «И– НЕ» |
|
|
|
|
|
||||||||
Функция |
Шеффера |
описывает |
работу |
элемента |
(вентиля) «И– НЕ» |
|||||||||||||
(рис. 46). В общем случае элемент «И– НЕ» может иметь n входов (рис. 4в). При этом он реализует функцию Шеффера от n переменных, т. е.
F = x1 x2 ... xn
Логическое сложение (дизъюнкция)
Логическое сложение – это логическая функция, по крайней мере, от двух переменных, которая принимает нулевое значение при нулевых значениях всех переменных. Функция логического сложения называется также дизъюнкцией. Возможные обозначения дизъюнкции:
x1 x2 ; x1 + x2 ; х1 ИЛИ х2; х1 OR х2.
Таблица истинности элементарной дизъюнкции представлена на рис. 5а. Элементарная дизъюнкция принимает единичное значение на наборах 1, 2, 3 и нулевое значение – только на наборе 0. Знак «плюс» не является алгебраическим, так как при х1=1, х2=1 дизъюнкция F = x1 + x2 = 1 , т. е.
она не может быть равной 2.
Дизъюнкция описывает функционирование элемента (вентиля) «ИЛИ» (рис. 5б). Единичный сигнал на выходе этого элемента возникает тогда, когда или на входе 1, или на входе 2, или на обоих входах есть единичные сигналы. И только в том случае, когда на оба входа поступают нулевые сигналы, на выходе элемента появляется нулевой сигнал. В общем случае элемент «ИЛИ» может иметь n входов (рис. 5в). При этом он реализует дизъюнкцию от n переменных.

9
x1 |
x2 |
F |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
. |
|
|
F |
||||||||
0 |
1 |
1 |
|
|
|
|
F |
|
|
||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
|
x2 |
|
|
|
. |
|
|
||||||||
|
|
|
|
||||||||||||
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
xn |
. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
б) |
|
|
|
|
|
в) |
||
Рис. 5. Элемент «ИЛИ»
Функция Пирса
Это логическая функция, по крайней мере, от двух переменных, которая принимает единичное значение при нулевых значениях всех переменных. Эта функция называется также функцией отрицания от дизъюнкции, функцией Вебба. Читается как «x1 стрелка Пирса x2». Элементарная функция Пирса зависит от двух переменных. Возможные варианты записи функции:
F = x1 ↓ x2 ; F = x1 x2 ; F = x1 + x2 .
Таблица истинности элементарной функции Пирса представлена на рис. 6а. Функция принимает единичное значение на наборе 0 и нулевые значения на наборах 1, 2, 3.
x1 |
x2 |
F |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
0 |
0 |
1 |
|
x1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
F |
. |
|
|
F |
|||||||
|
|
|
|
|
|||||||||||
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
||||
|
x2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
. |
|
|
||||||||
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
xn |
. |
|
|
|
||||
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
б) |
|
|
|
в) |
||||
|
|
|
Рис. 6. Элемент «ИЛИ– НЕ» |
|
|
|
|
|
|
||||||

10
Функция Пирса описывает работу элемента (вентиля) «ИЛИ– НЕ» (рис. 6б). Элемент «ИЛИ-НЕ» может иметь n входов (рис. 6в). При этом он
реализует функцию Пирса от n переменных, т. е. F = x1 Ú x2 Ú ... Ú xn .
Неравнозначность
Неравнозначность – это логическая функция от двух переменных, которая принимает единичное значение при разных по значимости переменных. Таблица истинности функции представлена на рис. 7а.
x1 |
x2 |
F |
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
F |
|
0 |
0 |
0 |
|
|
|
|||
|
=1 |
|
||||||
0 |
1 |
1 |
x2 |
|
|
|
|
|
|
|
|
|
|
||||
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
б) |
|
||
Рис. 7. Элемент «ИСКЛЮЧАЮЩЕЕ ИЛИ»
Неравнозначность ещё называют функцией сложения по модулю два. Сложить по модулю — это значит представить сумму в виде остатка от
деления ее на модуль. Запись функции: F = x1 Å x2 . Используя элементарные логические функции получим выражение: F = x1x2 + x1x2 .
Функцию неравнозначности ещё называют «ИСКЛЮЧАЮЩЕЕ ИЛИ». Эта функция реализуется одноименным элементом, условно-графическое обозначение которого представленным на рис. 7б [2].
Равнозначность (эквивалентность)
Равнозначность — это логическая функция от двух переменных, которая принимает единичное значение при одинаковых значениях переменных. Одинаковые по значению переменные называются равнозначными, поэтому функция носит название «равнозначность».
Запись функции: F = x1~x2. Используя элементарные логические функции получим выражение F = x1 x2 + x1 x2 = x1 Å x2 .
