Непрерывные случайные величины Функция и плотность распределения непрерывной случайной величины

Чтобы однозначно задать н.с.в., необходимо указать ее функцию распределения.

Определение. Случайную величину называют непрерывной, если ее функция распределения есть непрерывная функция с непрерывной производной.

Вероятность того, что н.с.в. примет значение из некоторого интервала, определяется формулой: .

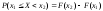Вероятность того, что непрерывная случайная величина примет некоторое конкретное значение равна нулю: .

Поскольку вероятность того, что н.с.в. примет конкретное значение, справедливо следующее равенство:

.

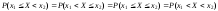Пример 1. Н.с.в. X задана функцией распределения 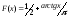. Найти вероятность того, что величина X примет значение, заключенное в интервале (0;1).

.

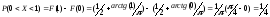Определение. Производная от функции распределения непрерывной случайной величины X называется плотностью распределения вероятностей X: .

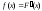Связь между функцией распределения и плотностью распределения:

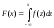
Свойства плотности распределения:

1. ;

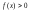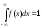2. (условие нормированности);

3. если все возможные значения н.с.в. лежат внутри интервала (a;b), то ;

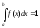4. вероятность того, что н.с.в. примет значение из некоторого интервала, равна .

Пример 2. Н.с.в. X задана плотностью распределения 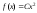на интервале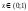. Найти константу C и вероятность того, что величина X примет значение, заключенное в интервале (0;0.5) и (0;2).

Исходя из условия нормированности н.с.в. .

.

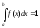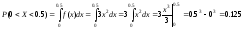
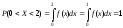
Числовые характеристики непрерывных случайных величин

Определение. Математическим ожиданием непрерывной случайной величины с плотностью распределения f(x) называется число:

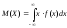, если указанный интеграл абсолютно сходится, в противном случае говорят, что математическое ожидание не существует.

Если н.с.в. определена на интервале (a;b), то математическое ожидание определяется по формуле:

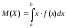
Все свойства математического ожидания дискретных случайных величин справедливы и для непрерывных случайных величин.

Определение. Дисперсией непрерывной случайной величины с плотностью распределения f(x) называется число:

.

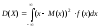Если н.с.в. определена на интервале (a;b), то дисперсия определяется по формуле:

.

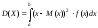Все свойства дисперсии дискретных случайных величин справедливы и для непрерывных случайных величин.

Для непрерывных случайных величин теорема 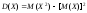может быть записана в виде: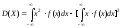

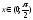Пример 3. Н.с.в. X задана функцией распределения на интервале. Найти математическое ожидание и дисперсию н.с.в. X.

Найдем плотность распределения: .

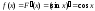Математическое ожидание: .

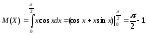Математическое ожидание квадрата с.в.: .

Дисперсия:

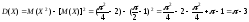
Определение. Мода – это значение абсциссы x_mod, при котором кривая плотности распределения имеет максимум. Мода указывает положение высоко вероятной области значений с.в.

Определение. Медиана – это значение абсциссы x_med, при котором фигура под кривой плотности распределения делится на две равновеликие части, площади которых равны по 0.5 каждая, то есть F(x_med)=0.5.

Определение. Квантиль – это значение абсциссы x_q, которое является решением уравнения F(x_q)=q.

Квантиль x_q называется q-ой или q·100-процентной квантилью функции распределения (или плотности распределения, или случайной величины). В частности медиана является 50-процентной квантилью.

Наиболее употребительные квантили:

квартиль - 25 - процентная квантиль, дециль - 10 - процентная квантиль.