05-04

!Taskfile kontr_СМ 2-05-04#Моменты инерции простых и сложных сечений

!De=kontr_СМ 2-05#Геометрические характеристики поперечных сечений стержня

!Task2

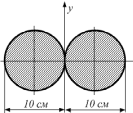
Момент инерции фигуры относительно оси y равен ____ см⁴.

!Solution

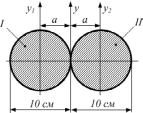
Разбивая фигуру на два круга и используя формулу, связывающую моменты инерции относительно параллельных осей, получаем

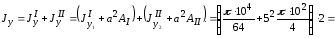
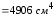
!True

!Task3

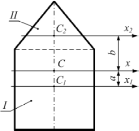
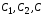− центры тяжестей прямоугольника, треугольника и всей фигуры. Момент инерции всей фигуры относительно оси x определяется по формуле …

!Solution

Сложную фигуру разбиваем на элементарные фигуры (прямоугольник и треугольник). Для элементарных фигур должны быть известны: положение центра тяжести; площадь; момент инерции относительно оси, проходящей через ее центр тяжести и параллельной оси x. Тогда, используя формулу, связывающую моменты инерции относительно параллельных осей, получаем

.

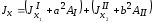!True

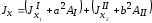
!Task5

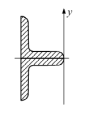
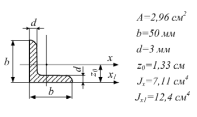
Поперечное сечение стержня составлено из двух равнобоких уголков. Характеристики поперечного сечения уголка известны. Момент инерции поперечного сечения стержня относительно оси y равен ___ см⁴.

!Solution

Разбиваем сечение на две элементарные фигуры (два уголка). Проводим оси y₁ и y₂, проходящие через центр тяжестей поперечных сечений углов и параллельные оси y. Оси y₁ и y₂ не совпадают с осью y, поэтому для вычисления момента инерции одного уголка относительно оси y используем формулу, связывающую моменты инерции относительно параллельных осей. Результат вычислений затем удваивается:

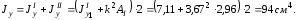
!True

!Task6

Размеры фигуры даны в мм. Момент инерции относительно оси x равен ___ мм⁴.

!Solution

Момент инерции определяем по формуле для прямоугольника

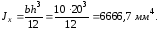
!True

6666,7

!Task7

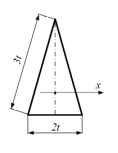
Момент инерции равнобедренного треугольника относительно оси x, проходящей через центр тяжести параллельно основанию, равен …

!Solution

Момент инерции определяем по формуле для треугольника

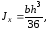где

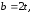
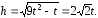
Подставляя значения b и h в формулу, получаем

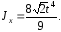
!True