Работа №7 потери напора на внезапном расширении

1. Цель и задачи работы

Задачей работы является экспериментальное изучение закономерностей потерь напора и распределения давлений в местных сопротивлениях, конкретным видом которых является внезапное расширение трубы. По результатам измерения строятся графики распределения давлений по длине трубы, определяется коэффициент местного сопротивления и строится участок графика его зависимости от числа Рейнольдса.

2. Основные положения и расчетные зависимости

Местные сопротивления представляют собой короткие участки трубопроводов, на которых скорости потока изменяются по величине и направлению в результате изменения размеров или формы сечений трубопровода.

Потери механической энергии в местных сопротивлениях, отнесенные к единице веса протекающей жидкости, называются местными потерями напора.

К местным сопротивлениям относятся: вход в трубу, расширение трубопровода (внезапное или постепенное), сужение трубопровода (внезапное или постепенное), поворот, колено, запорные устройства (краны, вентили, задвижки), решетки, фильтры и т. д.

Местные потери, так же как и потери по длине, обусловлены работой сил трения, но эти силы трения в узлах резко изменяющегося движения, свойственных «местным сопротивлениям», распределяются в потоке весьма неравномерно.

Такие места потока в общем случае характеризуются:

1. местными искривлениями линий тока и живых сечений,

2. уменьшением или увеличением живых сечений вдоль потока,

3. возникновением местных отрывов транзитной струи от стенок русла, а следовательно, появлением водоворотных областей.

В пределах такого рода узлов, а также в пределах некоторого расстояния за ними наблюдаем деформацию эпюр осредненных скоростей вдоль потока, повышение пульсации скоростей и давлений. Повышение пульсации скоростей обуславливает увеличение касательных турбулентных напряжений, что, в свою очередь, влечет за собой повышение потерь напора. Таковы условия возникновения местных потерь напора.

Местные потери обычно выражаются в долях скоростного напора и определяются по формуле Вейсбаха:

_{где ξ – коэффициент местного сопротивления, υ – средняя скорость в трубе обычно за сопротивлением.}

_{Коэффициенты местных сопротивлений ξ зависят от геометрических параметров того или иного местного сопротивления, являются величинами эмпирическими (за исключением внезапного расширения, которое можно определить по теореме Борда), их расчетные значения приведены в справочной и учебной литературе.}

_{Коэффициенты местных сопротивлений в трубопроводах мало меняются с изменением числа Рейнольдса поэтому считают, что они практически не зависят от Числа Рейнольдса.}

_{Экспериментально, в лабораторных условиях, местные потери напора можно определить из уравнения Бернулли, составленного для двух сечений, находящихся перед сопротивлением и после сопротивления.}

_{Определив экспериментально величину местных потерь и подставляя их в формулу Вейсбаха, можно определить экспериментальное значение коэффициента местного сопротивления.}

_{В данной работе предлагается определить коэффициент местного сопротивления внезапного расширения.}

Теорема Борда: Потеря напора при внезапном расширении равняется скоростному напору, отвечающему потерянной скорости: ,

где и - средние скорости в исследуемых сечениях. Используя уравнения неразрывности, эту формулу можно представить в виде

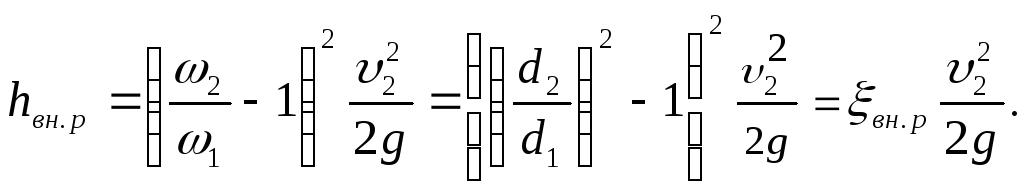
_или

,

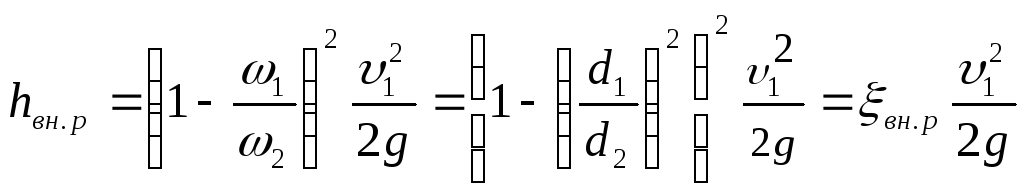где и- площади нормальных сечений;- коэффициент потерь на внезапном расширении.

Следует подчеркнуть, что последняя формула получена из теоретиче­ской схемы, в которой игнорируются потери трения, а также пред­полагается равномерное распределение скоростей в сечениях труб. Поэтому коэффициент оказывается независимым от числа Рейнольдса, а сама формула отражает лишь так называемый квадратич­ный участок кривой, где в реальных условиях влияние числа Рейнольдса отсутствует.

Существует, по крайней мере, два подхода к эксперименталь­ному определению коэффициента потерь при внезапном расшире­нии. Первый состоит в его определении по измерениям давлений и скоростей в двух контрольных сечениях. При таком способе учитывается не только потери на внезапном расширении, но и поте­ри трения на контрольном участке. Согласно другому подходу, из полного коэффициента исключаются потери на трение, что можно сделать с помощью построения линии энергии по длине участка расширения путем вычисления потерь на трение по формуле равно­мерного движения или по данным опытов на специально оборудо­ванной установке.