plan_exp

где t - критерий Стьюдента, определяемый по таблице приложения П4 в зависимости от числа степеней свободы n = N(m-1) и уровня значимости, который для инженерных расчетов принимается равным 5%.

В нашем случае

n = 16 (3 - 1) = 32

Поскольку в таблице П4 значение n = 32 отсутствует, рекомендуется находить t путем интерполяции между значениями этой величины для n = 30 и n = 40. Тогда t = 2,038, а

SAt = 0,394 × 2,038 = 0,803

Таким образом, значимы лишь те коэффициенты регрессии, которые по абсолютной величине удовлетворяют условию (29).

В нашем примере коэффициент, меньший этой величины, отбрасывается - это коэффициент А4. 17. Окончательно уравнение регрессии примет вид

y = А0 + А1Х1 + А2Х2 + А3Х3 + А12Х1Х2 + А13Х1Х3 + А14Х1Х4 +

+А23Х2Х3 + А24Х2Х4 + А34Х3Х4 = 110,8-1,96 Х1 + 3,88 Х2 -

-2,17 Х3 - 2,58 Х1Х2 - 3,38 Х1Х3 - 0,844 Х1Х4 + 1,46 Х2Х3 -

-1,46 Х2Х4 + 3,67 Х3Х4

18.Значения y после уточнения также приведены в таб. 6.

19.Дисперсия неадекватности определяется по формуле

где С - количество значимых коэффициентов регрессии

y€n - теоретическое значение выходной величины, в нашем примере рассчитывается по форму-

ле п.17.

20. Критерий Фишера

При этом количество значимых коэффициентов регрессии определяется из формулы п.17, а сумма квадратов отклонений определяется суммированием значений соответствующего столбца.

В свою очередь

F = sнад2 = 88,7 = 4,69

S2 18,9

Полученное расчетное значение критерия Фишера сравнивается с табличным, полученным в зависимости от числа степеней свободы n1 = N - C и n2 = N(m-1) по таблице приложения П5.

Если Fрасч £ Fтабл , то полученная математическая модель адекватно описывает процесс.

В нашем примере при n1 = 16-10 = 6 и n2 = 16 × 2 = 32, Fтабл = 2,32 и поэтому Fрасч > Fтабл, что говорит о том, что математическая модель неадекватно описывает процесс.

Какое решение должен принять экспериментатор? Как сделать модель адекватной? Обычно идут по линии усложнения моделей, т.е. повышения порядка полинома, для чего потребуются более сложные модели, о которых речь пойдет в дальнейшем.

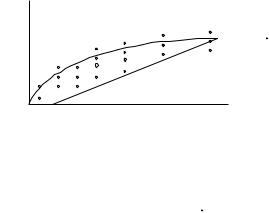
Следует также отметить, что оценка адекватности по Фишеру не всегда эффективна, т.к. в соответствии с этим критерием уравнение адекватно описывает процесс только в том случае, если кривая находится внутри зоны расположения экспериментальных точек (рис. 3).

разброс точек, тем труднее ему получить адекватное уравнение. Поэтому в ряде случаев исследователи отвергают подход Р. Фишера к определению адекватности модели и поль-зуются подходом Закгейма [35], который заключается в том, что задается допустимым отклонением величины y в %.

Если во всех точках плана отклонение расчетного значения у от экспериментального не превышает допустимого, то считают, что модель адекватно описывает процесс.

Таким образом при достаточно точном эксперименте следует пользоваться подходом Закгейма, при невысокой точности подходом Фишера.

В рассмотренном примере (табл.6), если задаться допустимой точностью модели5%, то лишь в двух точках 4 и 8 отклонения превышают заданные значения и только в этих точках уравнение неадекватно описывает процесс. Как правило экспериментатор этим удовлетворяется. В более ответственных случаях целесообразно найти уравнение поверхности, ограничивающей область адекватного представления модели.

2.5.Дробный факторный эксперимент (ДФЭ)

Сувеличением числа факторов количество необходимых для получения математической модели

опытов растет. Для плана полного факторного эксперимента, как было сказано выше, число опытов N=2к. Уже при к=6 N=26=64, что в большинстве случаев совершенно неприемлемо для экспериментатора. Поэтому возникает необходимость в уменьшении числа фактов.

Вместе с тем для определения коэффициентов регрессии можно обойтись меньшим количеством опытов, если, использовать планы дробного факторного эксперимента, которые представляют собой некоторую часть (1/2; 1/4; 1/8; 1/16) от полного факторного эксперимента. Примером такого плана может служить план для четырех факторов, представленный в таблице 7.

Таблица 7.

План ДФЭ для четырех факторов.

Основу плана составляет план для трех факторов типа 23. Столбец для фактора Х4 получается с помощью соотношения Х4=Х1Х2Х3. При этом предполагается, что тройным взаимодействием Х1Х2Х3 можно пренебречь. Можно также воспользоваться соответствием Х4=-Х1Х2Х3.

Произведение столбцов, дающее во всех строчках +1(или -1), называется определяющим контра-

стом. В нашем примере определяющий контраст ХХ Х Х =1. С его помощью нетрудно определить,

1 2 3 4

какие эффекты смешаны. Чтобы выяснить, например, с чем смешан эффект Х обе части определяю-

1

щего контраста умножают на Х1. Тогда Х1= Х2Х3Х4 (так как), X12 т.е. фактор Х1 смешан с взаимодействием Х2Х3Х4. Последнее равенство, как и равенство Х4= Х1Х2Х3 называется генерирующим соотношением. Т.к. практически тройным взаимодействием можно пренебречь, то применение таких планов вполне оправдано.

План, представленный в таблице 7, является частью, половиной полного факторного эксперимента для четырех факторов или, как говорят его дробной репликой. В общем случае дробной репликой называют 1/2n часть полного факторного эксперимента, полученную путем замены одного или -не скольких взаимодействий новым фактором. Условно тип дробного факторного эксперимента записывается как 2к-р, где к - число факторов, а р - количество линейных факторов, приравненных к эффектам взаимодействия.

Планы, у которых в определяющем контрасте больше факторов, имеют большую разрешающую способность. Иногда план ДФЭ, представленный в таблице 7 записывается в виде 24IV-1 , где римская цифра IV определяет разрешающую способность плана.

Пример: Пусть требуется составить план25V-1. Так как разрешающая способностьV, то определяющий контраст записывается в виде соотношения Х1Х2Х3Х4Х5=1, а генерирующее соотношение Х5 = Х1Х2Х3Х4.

Таблица 8.

План ДФЭ для пяти факторов.

Коэффициенты регрессии для планов ДФЭ определяются по тем же формулам, что и для ПФЭ. Однако, следует помнить, что для взаимодействий, которые коррелируют с какими-либо факторами, коэффициенты регрессии не рассчитываются. При корреляции двойных и тройных взаимодействий последние также не рассчитываются и т.д.

2.6. План взвешивания

Пусть требуется взвесить с достаточной точностью7 предметов. Предположим, что веса предметов Х1, Х2, Х3, Х4, Х5, Х6, Х7. Взвесим все предметы вместе. Тогда их общий вес

у1= Х1 + Х2 + Х3 + Х4 + Х5 + Х6 + Х7

Затем будем взвешивать по три предмета и получим

Каждый предмет находится на чаше весов4 раза. Благодаря этому повышается точность при том же числе взвешиваний. Кстати это не единственный способ четырехкратного взвешивания каждого предмета. Можно, например, начиная, со второго опыта взвешивать три следующих друг за другом предмета. Тогда

Точность взвешивания можно увеличить если при каждом взвешивании использовать все предметы. Для этого те из них, которые в предыдущей системе отсутствуют можно в нее добавить со знаком “ - ”. Тогда

Таблица 9.

План взвешивания (план Хаутелинга)