Лабораторная работа № 124 определение скорости звука в воздухе методом стоячих волн

Цель работы

Определение скорости звука в воздухе и отношения теплоемкостей для воздуха.

Теоретическое введение

Волны. Если источник колебаний находится в какой - либо упругой среде, то вследствие взаимодействия между ее частицами колебания будут передаваться от частицы к частице и перемещаться в пространстве с некоторой скоростью V_в. Процесс распространения колебаний в пространстве называется волной. Частицы среды, в которой распространяется волна, не перемещаются в пространстве поступательно вместе с волной, а лишь колеблются около своих положений равновесия. При этом происходит передача энергии от источника колебаний в пространство без переноса вещества.

В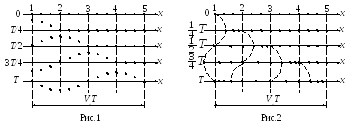олны бывают продольные и поперечные. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны (рис.1), а в продольной - вдоль направления распространения волны (рис.2).

В твердой среде могут возникать продольные и поперечные волны, в жидкостях и газах - лишь продольные волны. В жидкостях поперечные волны могут существовать только на поверхности, вследствие сил поверхностного натяжения.

Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны (или волновым фронтом). Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновых поверхностей существует бесконечное множество, в то время как волновой фронт в каждый момент времени только один.

В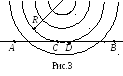простейших случаях волновые поверхности имеют форму плоскости или сферы. Соответственно волна называется плоской или сферической. Одна и также волна может считаться плоской или сферической в зависимости от условий опыта, как показано на рис.3. Если в опыте база наблюдения волны сравнима с радиусом кривизныR волновой поверхности или больше его, как это имеет место для базы АВ, то волну следует считать сферической.

Если база наблюдения значительно меньше радиуса кривизны, как в случае базы СD, волну следует считать плоской.

Звуковыми волнами (или звуком) называются упругие волны, распространяющиеся в среде и имеющие частоты от 20 до 20000 Гц. Звуковые волны, достигнув человеческого уха, вызывают ощущение звука.

Звуковые волны с частотами, меньшими 20 Гц, называются инфразвуком; волны с частотами, превышающими 20000 Гц, называются ультразвуком.

Звуковая волна в газе является продольной и представляет собой распространяющуюся в пространстве последовательность чередующихся областей сжатия и разрежения.

Уравнение волны. Уравнением волны называется выражение, которое дает зависимость смещения колеблющейся точки (около ее положения равновесия) от координат и времени.

Р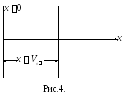ассмотрим плоскую волну, распространяющуюся вдоль осиХ(рис.4).

Пусть колебания точек, лежащих в плоскости x0, описываются уравнением

,

где a - амплитуда, ₀ - циклическая частота.

Если волна распространяется со скоростью V_в, то до точек, находящихся от этой плоскости на расстоянии x, колебания дойдут через время τ  x/V_в. Следовательно, в точках принадлежащих плоскости x они будут отставать по фазе на ₀τ от колебаний частиц в плоскости x  0. Уравнение колебания частиц, лежащих в плоскости x, будет иметь вид

,

или, с учетом τ  x/V_в:

.

Чтобы фаза волны была записана симметрично относительно t и x, внесем ₀ за скобки и введем обозначение k ₀/V_в, где k – волновое число:

.

Таким образом, уравнение плоской волны имеет вид

(1)

Найдем еще одно выражение для волнового числа k. Между периодом колебаний Т, частотой ν и циклической частотой ₀ имеется связь:

. (2)

За один период колебаний волна перемещается на расстояние, называемое длиной волны λ:

λ  V_вТ.

С учетом соотношений (2)

,

откуда следует

.

У сферической волны амплитуда колебаний убывает обратно пропорционально расстоянию r от источника колебаний: а  а₀/r, где а₀ – величина, численно равная амплитуде колебаний на расстоянии, равном единице длины от источника. Заменив x на расстояние r в фазе волны, можно записать уравнение сферической волны

. (3)

Уравнение (3) справедливо при r, значительно превышающем размеры источника, так как при стремлении r к нулю амплитуда колебаний неограниченно возрастает.

Скорость распространения упругих волн. Рассмотрим распространение продольной волны в упругом стержне безотносительно к материалу, из которого он состоит, в частности, это может быть столб газа в трубе. Пусть на поперечное сечение S стержня действует деформирующая сила F (рис.5), под действием которой за время Δt левый конец стержня сместился на расстояние . Скорость сместившихся частиц стержня равна

. (4)

Пусть за это время волна сжатия, распространяясь с большей скоростью, чем смещаются частицы, пройдет расстояние . Следовательно, скорость волны будет равна

. (5)

Д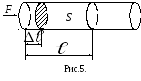ля деформированной части стержнясправедлив закон Гука

, (6)

где Е – модуль Юнга, равный усилию, которое нужно приложить к стержню единичной площади сечения, чтобы вдвое изменить его длину.

Импульс силы, деформировавшей стержень в течение времени Δt, равен

. (7)

За счет импульса силы деформированная часть стержня получила импульс движения , гдеm –масса частиц, пришедших в движение за время Δt . Массу частиц можно выразить через плотность стержня ρ следующим образом:

.

Тогда, с учетом формул (4) и (5),

. (8)

Так как импульс силы, действующей на тело, равен изменению импульса его движения , то, сравнивая правые части равенств (7) и (8), получим

. (9)

Таким образом, скорость волн в среде зависит от ее упругих свойств и плотности.

Термодинамика звуковых колебаний. Зная скорость звука в воздухе, можно определить важный термодинамический параметр – отношение теплоемкостей воздуха при постоянном давлении и постоянном объеме.

Запишем закон Гука (6) в следующем виде:

, (10)

где p  F/S представляет давление звуковой волны в области сжатия.

Если сжатие воздушного столба происходит без изменения его поперечного сечения, то справедливо следующее соотношение:

,

где V- объем воздуха, а ΔV- его изменение.