7. Доверительные интервалы для математического ожидания и дисперсии

В пункте 3 был рассмотрен вопрос об оценке неизвестного параметра распределения одним числом. Такую оценку называют точечной. Однако часто требуется найти не только приближенное значение параметра, но и оценить его точность и надежность. Для этого в математической статистике пользуются доверительными интервалами.

Пусть для параметра из опыта получена несмещенная оценкаЗададимся вероятностьюp, такой, что событие, происходящее с этой вероятностью, можно было бы считать практически достоверным (обычно эти значения берут равными 0,9; 0,95; 0,99) и найдем такое значение для которого

(9.28)

или

Интервал называютдоверительным интервалом, а p – доверительной вероятностью; число называютуровнем значимости. Границы интервала называют доверительными границами.

Надо отметить, что является случайным, так как случайно его положение на оси абсцисс, определяемое центромслучайна и его длинатак как величинаопределяется из опытных данных. Таким образом, величинуp можно интерпретировать как вероятность, с которой интервал накроет истинные значения параметраКроме того,можно считать множеством значений параметрасовместимых с опытными данными и не противоречащих им.

Пусть подтвердилась гипотеза о нормальном законе распределения случайной величины X. Тогда доверительный интервал для параметра или, что то же самое, (см.(7.25), (9.6) и (9.15)) для математического ожидания имеет вид

(9.29)

где – оценка параметра;– несмещенное среднеквадратичное отклонение;

n – объем выборки; – коэффициент, который находят, пользуясь табл.6 Приложения по выбранной доверительной вероятностиp и числу степеней свободы

Доверительный интервал для дисперсии в указанной выше ситуации имеет вид

(9.30)

где n – объем выборки; – несмещенная оценка дисперсии (см.(9.8));

p – доверительная вероятность; – значение, которое находят, пользуясь табл.3 (или 3.а) Приложения по вероятностии числу степеней свободы, равным

–значение, которое находят, пользуясь табл.3 или 3а Приложения по вероятности и числу степеней свободы

Пусть теперь случайная величина X имеет закон распределения, отличный от нормального. Тогда доверительный интервал для математического ожидания приближенно имеет вид

(9.31)

где – оценка математического ожидания;p – доверительная вероятность;

–среднее квадратическое отклонение выборочного среднего,

(9.32)

–коэффициент, который находят по табл.2 Приложения как значение аргумента, при котором функция Лапласа равна

Совершенно аналогично может быть построен доверительный интервал для дисперсии:

(9.33)

где – несмещенная оценка дисперсии (см.(9.8));– коэффициент, который находят так же , как в формуле (9.31);– среднее квадратическое отклонение несмещенной выборочной дисперсии .

Для нахождения можно воспользоваться тем, чтогдеn – объем выборки.

В этой формуле неизвестную DX можно заменить на приближенное значение – также можно заменить его оценкой:

Если нет оснований считать, что закон распределения случайной величины X резко отличается от нормального, то можно воспользоваться формулой

(9.34)

Кроме того, если подтвердилась гипотеза о равномерном законе распределения, то можно воспользоваться формулой

(9.35)

Далее приведены примеры, иллюстрирующие проверку гипотезы о законе распределения и построение доверительного интервала для математического ожидания и дисперсии.

Пример 3. Получена выборка из генеральной совокупности

42,54	48,56	62,55	69,26	52,12	56,16	61,17	58,97	64,45	56,28
66,28	58,07	65,04	62,72	63,96	56,72	64,96	55,80	48,31	35,84
49,90	45,53	48,26	46,24	63,18	44,89	57,23	68,22	54,04	73,46
53,91	46,38	71,06	49,27	40,48	69,86	75,85	51,32	42,93	55,00
72,77	61,13	60,40	63,71	38,82	61,02	75,92	53,44	76,33	35,26
38,88	70,45	53,61	65,08	51,59	53,07	51,41	62,40	50,81	65,11
51,99	63,58	61,00	51,38	61,38	54,90	58,05	48,70	66,70	43,37
53,52	45,04	55,81	55,99	60,60	57,75	48,89	58,00	50,22	54,84
58,84	61,38	46,34	43,26	64,91	32,68	53,00	46,72	52,72	63,82
48,88	52,70	52,21	72,72	53,24	52,72	45,23	49,79	43,43	68,50

По этой выборке получаем вариационный ряд

32,68	43,43	48,31	50,81	53,00	55,00	58,05	61,38	63,96	69,26
35,26	44,89	48,56	51,32	53,07	55,80	58,07	61,38	64,91	69,86
35,84	45,04	48,70	51,38	53,24	55,81	58,84	62,40	64,96	70,45
38,82	45,23	48,88	51,41	53,44	55,99	58,97	62,45	65,04	71,06
38,88	45,53	48,89	51,99	53,52	56,16	60,40	62,55	65,08	72,72
40,48	46,24	49,27	52,12	53,61	56,28	60,60	62,72	65,11	72,77
42,54	46,24	49,79	52,21	53,61	56,72	61,00	63,18	66,28	73,46
42,93	46,38	49,90	52,70	54,04	57,23	61,02	63,58	66,70	75,85
43,26	46,72	50,22	52,72	54,84	57,75	61,13	63,71	68,22	75,92
43,37	48,26	50,59	52,72	54,90	58,00	61,17	63,82	68,50	76,33

Диапазон наблюденных значений случайной величины X укладывается в интервал (32;77). Разбиваем интервал наблюдений значений случайной величины на 9 разрядов с шагом

Дальнейшие шаги рассмотрены ранее в пунктах 2-6. В результате, после их выполнения, получаем таблицу 5 и рис.5.

Таблица 5
1		3	3	13	16	22	15	16	6	6
2		0,03	0,03	0,13	0,16	0,22	0,15	0,16	0,06	0,06
3		0,006	0,006	0,026	0,032	0,044	0,030	0,032	0,012	0,012
4		34,5	39,5	44,5	49,5	54,5	59,5	64,5	69,5	74,5
5		-2,22	-1,70	-1,18	-0,66	-0,14	0,39	0,91	1,43	1,95
6		0,0339	0,0940	0,1989	0,3209	0,3961	0,3697	0,2637	0,1435	0,0596
7		0,004	0,010	0,021	0,033	0,041	0,039	0,028	0,015	0,006
8		0,020	0,050	0,105	0,165	0,205	0,195	0,140	0,075	0,030
9		2	5	10,5	16,5	20,5	19,5	14	7,5	3
10		-1		2,5	-0,5	1,5	-4,5	2	1,5	3
11		1		6,25	0,25	2,25	20,25	4	2,25	9

Комментарии к табл.5.

Используя информацию в строках 1-3, строим гистограмму, вид которой позволяет выдвинуть гипотезу о нормальном законе распределения исследуемой случайной величины.

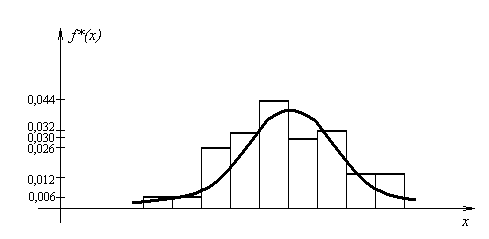
Рис.5. Гистограмма и выравнивающая ее функция плотности

Результаты расчетов в строках 4-7 дают возможность построить ни гистограмме выравнивающую кривую функции плотности. Отметим, что предварительно, для вычислений значений функции плотности, были найдены точечные оценки математического ожидания (см.(9.9)) и дисперсии (см.9.11)), что, согласно (9.15), позволило получить и оценки параметров и

Для данного примера имеем

В 8-й строке приведены результаты вычислений по формуле (9.27).

В первом и во втором разрядах оказалось менее 5 наблюдений, поэтому объединим эти разряды в один.

По результатам вычислений, приведенных в строках 9-11, вычисляем по формуле (9.23) значение

Определим по формуле (9.22) число степеней свободы - параметр распределения Учитывая, что число наложенных связей для нормального распределения равно 3, а число разрядов уменьшилось на один, то число степеней свободыВыберем уровень значимостии по таблице 3 Приложения длянайдемТак как наблюденное значениеоказалось меньше табличного значения, то есть произошло событиевероятность которого равна 0,95, то можно сделать вывод: выдвинутая гипотеза о нормальном законе распределения не противоречит опытным данным.

Построим доверительный интервал для математического ожидания по формуле (9.29). Зададимся доверительной вероятностью и, учитывая, что число степеней свободыпо табл.6 найдемтогдаили

Построим доверительный интервал для дисперсии по формуле (9.30). Зададимся доверительной вероятностью тогдачисло степеней свободыТогда по таблице 3а находимтаким образом,илиследовательно, истинное значениеслучайной величиныX находится в этом интервале с вероятностью 0,95.

Пример 4. В механическом цехе с десятью станками в течение определенного периода ежедневно регистрировали количество выбывших их строя станков, проведя 200 наблюдений. Предполагается, что случайная величина X – число отказавших станков – удовлетворяет распределению Пуассона, так как в нормальных условиях производства отказ станка можноь считать редким событием, которое не зависит от отказа других станков. Подтверждает ли выборка, представленная в табл.6, эту гипотезу?

Таблица 6
Число отказов станков,	Частота отказов,	Относительная часота отказов,
0	41	0,205
1	62	0,31
2	45	0,225
3	22	0,11
4	16	0,08
5	8	0,04
6	4	0,02
7	2	0,01
8	0	0
9	0	0
10	0	0
	n=200

Чтобы использовать критерий надо по значениям выборки найти значение параметраа распределения Пуассона и вычислить теоретические частоты Согласно (9.13), оценкойа будет выборочное среднее

Для примера 4 вычисленное по формуле (9.9):

Вероятности вычислены по формуле (9.21) с учетом того, что

Все промежуточные результаты для вычисления значения представлены в табл.7.

Таблица 7
Число отказов станков	Частота	Относит. частота	Вероятность	Теорет. частота
0	41	0,2050	0,1653	33,06	7,94	63,0436	1,91
1	62	0,3100	0,2975	59,5	2,5	6,25	0,11
2	45	0,225	0,2678	53,56	8,56	72,2736	1,37
3	22	0,1100	0,1607	32,14	10,14	102,8196	3,2
4	16	0,0800	0,0723	14,46	1,54	2,3716	0,16
5 6 7 8 9 10		0,0400	0,0260		6,72	45,1584	6,2
		0,0200	0,0078
		0,0100	0,0020
		0	0,0005
		0	0,0001
		0	0,0000
	200	1	1	200

В этом примере объдинены последние 6 разрядов. Число степеней свободы, с учетом (9.22), так как по выбоке оценивался неизвестный параметра. Выбираем уровень значимости Пользуясь табл. 3 Приложения поинаходимТак както гипотезу о распределении Пуассона надо отвергнуть, следовательно, выборка взята из генеральной совокупноти, распределение которой не подчиняется закону Пуассона.

На рис. 6 представлены многоугольники распределения относительных частот и вероятностей.

Рис.6. Многоугольник распределения;

многоугольник распределения .

Построим доверительные интервалы для MX и DX. С учетом формул (7.20) имеем: Тогда по формуле (9.32) получаемВозьмем доверительную вероятностьи по табл. 2 Приложения найдем значениекак значение аргумента, при котором функция Лапласа равнатогда, используя формулу (9.31), получаем доверительный интервал дляMX: или

Для построения доверительного интервала для дисперсии по формуле (9.34) найдем

Тогда доверительный интервал для дисперсии, найденный по формуле (9.33), имеет вид

или

Пример 5. Имеем результаты наблюдений изучаемой случайной величиныX

0,03	0,11	0,64	0,35	0,13	0,01	0,27	0,01	0,22	0,92
0,01	0,64	0,77	0,92	0,48	0,03	0,04	0,25	0,39	0,97
0,06	0,19	0,47	0,32	0,48	0,11	0,11	0,19	0,80	0,26
0,12	0,11	0,20	0,98	0,56	0,08	0,01	0,57	0,47	0,84
0,05	0,49	0,12	0,14	0,36	0,19	0,06	0,37	0,09	0,98
0,07	0,09	0,07	0,07	0,34	0,02	0,04	0,68	0,27	0,53
0,01	0,23	0,84	0,21	0,63	0,55	0,05	0,36	0,15	0,84
0,18	0,01	0,66	0,74	0,36	0,08	0,22	0,57	0,35	0,12
0,21	0,52	0,25	0,03	0,11	0,78	0,07	0,34	0,93	0,04
0,14	0,02	0,12	0,35	0,50	0,24	0,03	0,70	0,68	0,21

Расположим эти наблюдения не в порядке получения, а в порядке их возрастания, получим вариационный ряд.

0,01	0,03	0,07	0,11	0,18	0,23	0,35	0,48	0,63	0,80
0,01	0,03	0,07	0,11	0,19	0,24	0,35	0,48	0,64	0,84
0,01	0,04	0,07	0,12	0,19	0,25	0,35	0,49	0,64	0,84
0,01	0,04	0,08	0,12	0,19	0,25	0,36	0,50	0,66	0,84
0,01	0,04	0,08	0,12	0,20	0,26	0,36	0,52	0,68	0,92
0,01	0,05	0,09	0,12	0,21	0,27	0,36	0,53	0,68	0,92
0,02	0,05	0,09	0,13	0,21	0,27	0,37	0,55	0,70	0,93
0,02	0,06	0,11	0,14	0,21	0,32	0,39	0,56	0,74	0,97
0,03	0,06	0,11	0,14	0,22	0,34	0,47	0,57	0,77	0,98
0,03	0,07	0,11	0,15	0,22	0,34	0,47	0,57	0,78	0,98

Исходные данные удобно разбить на 10 разрядов с шагом Выполняя последовательно пункты этого параграфа, получим таблицу 8.

Таблица 8
1		27	18	12	11	6	6	7			6
2		0,27	0,18	0,12	0,11	0,06	0,06	0,07	0,04	0,03	0,06
3		2,7	1,8	1,2	1,1	0,6	0,6	0,7	0,41	0,31	0,62
4		0,05	0,15	0,25	0,35	0,45	0,55	0,65	0,75	0,85	0,95
5		2,604	1,923	1,421	1,049	0,775	0,572	0,423	0,312	0,231	0,170
6		0,253	0,187	0,138	0,102	0,075	0,056	0,041	0,030	0,022	0,017
7		25,259	18,656	13,780	10,178	7,517	5,552	4,101	3,029	2,237	1,7
8		3,031	0,431	3,167	0,676	2,302	0,201	8,404	0,943	0,582	18,49
9		0,120	0,023	0,230	0,066	0,306	0,036	2,049			10,876

Пояснения к табл.8.

В-первых трех строках последовательно определены выборочные частоты относительные частотыи высотыстолбцов гистограммы по формулам (9.4), (9.5) соответственно. По результатам вычислений третьей строки построена гистограмма, представленная на рис.7.

Рис.7. Гистограмма и выравнивающая ее кривая функции плотности

Исходя из вида гистограммы, выдвигаем гипотезу о показательном законе распределения, функция плотности которого имеет вид (7.21).

Найдем оценки MX и DX по формулам (9.9), (9.11) соответственно. Так как

то

С учетом формулы (7.22), имеем оценку параметра закона распределения:Значения функции плотности получаем по формуле (7.21), заменяяего оценкойи беря в качествеx для i-го разряда Вероятностинаходим по формуле (9.27). Вычисления, выполненные в 7-й, 8-й и 9-й строках очевидны.

По формуле (9.23) находим значение а по формуле (9.22) определяем число степеней свободыr с учетом объединения разрядов и числа параметров закона распределения, оцениваемых по выборке: Возьмем уровень значимостипо табл. 3 найдем критическое значениеа по формуле (9.22) определяем число степеней свободыr с учетом объединения разрядов и числа параметров закона распределения, оцениваемых по выборке: Возьмем уровень значимостипо табл. 3 найдем критическое значениеСогласно (9.24), произошло событие, вероятность которого равна 0,05, то есть гипотеза о показательном распределении противоречит опытным данным, а потому должна быть отвергнута.

Найдем доверительные интервалы для MX и DX. По формуле (9.32) а по формуле (9.34)Тогда для доверительной вероятностинайдем значениепо табл. 2 Приложения как значение аргумента функции Лапласа, при котором она равнаИ по формулам (9.31) и (9.33) получаем соответственноилииили