Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алматинский университет энергетики и связи

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Кванттык механикагакириспе

.pdf

Скачиваний:

Добавлен:

01.05.2015

Размер:

1.3 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

w = w(к0 ) + к - к0 )

¶w

к = к

(к - к0 )2

¶2 w

к = к0

+ ... = w0 + w1 + w2 ...

¶к

¶к2

(2.12)-ші қатардың алғашқы

екі

мүшесімен

шектелелік, w = w0

ретті аз шама деп ескермеген мүшеміз:

w2	=	(к - к	0 ) 2	¶2 w
		2		¶к2

Сонда (2.11) толқындық функция мынадай түрге келеді:

Y(x, t) = Be−i( w0t −к0 x)

мұнда B = A sinξ ξ

(2.12)

+ w1 . Екінші

(2.13)

(2.14)

(2.15)

ξ =	к (x - w¢		× t)	(2.16)
	2	0
	2

(2.15), (2.16)-шы қатынастардан микробөлшек қозғалысын сипаттайтын толқындық пакеттің кеңістікте де, уақыт бойынша да тұрақты болмайтындығын көреміз. Енді толқыңдық пакеттің қозғалыс жылдамдығын табу үшін амплитуданың белгілі бір мəнінде ξ

ξ =

соnst

(2.17)

w¢

деп қарастырып, бұдан жылдамдық U

= ∂x = w¢ =

∂w

(2.18)

¶t

¶к

Толқындық

пакеттің кеңістікте

шоғырлануын

қарастыралық. (2.17)-ші

өрнектен

t = 0 деп алсақ, онда

ξ =

к x

(2.19)

Толқындық пакеттің амплитудасының квадраты, өзінің максимум мəніне ξ ® 0

болғанда жетеді:

B 2 = A2

(2.20)

Амплитуда

квадратының

басқа

салыстырмалы

максимумдерінің

мəндері

ξ = ±

3π

,±

5π

,±

7π

... үшін амплитудалар:

3π

5π

, B

= A

,...

(2.21)

9π 2

25π 2

Ал, ξ = ±π ,±2π ,... мəндерінде толқындық пакеттің амплитудасы нольге тең.

Толқындық пакеттің кеңістікте шоғырлануының негізгі облысы [-π ,+π ] аралығы.

Яғни

ξ =

(2ξ 0 ) =

Dk × Dx = π

(2.22)

Бірақ толқындық пакеттің амплитудасы бұл облыстың сыртында да нольден өзгеше болатындықтан (2.22) теңдікті теңсіздікпен алмастыралық:

Dk × Dx ³ 2π

(2.23)

(2.23)-шы өрнектен монохроматты жазық толқындардан кұрылған толқындық пакеттің микробөлшектердің қозғалысын сипаттай алмайтындығын көреміз. Енді толқындық пакеттің уақыт бойынша шоғырлануын қарастыралық, ол үшін (2.16) қатынастан х = 0 деп алсақ

	ξ = -			k × w			(2.24)
				2
Жоғарыдағы талдауды қайталасақ, төмендегі қатынасқа келеміз
	Dw × Dt ³ 2π						(2.25)
Толқындық пакеттің кеңістікте таралуында екінші ретті аз							шама деп ескерілмеген
мүшенің толқындық процеске тигізетін əсерін қарастыралық:
w2 =	(k - k	0 )2	×	¶2 w	k	= k 0

	2!			¶k 2

Егер толқындық пакеттің дисперсиясы болмай, яғни пакет тек монохроматты жазық толқындардан тұрса, онда (2.13) теңдеуді ескермеуіміз дұрыс. Себебі, мұндай кеңістікте пакет өзгермейді, тұрақты фазалық жылдамдықпен қозғалады. Керісінше, дисперсия құбылысы болса, онда (2.13) мүшені ескермеу мүмкін емес, себебі мұндай толқындық пакеттің фазалық жылдамдығы тұрақты болмайды, толқындық пакеттің формасы уақыт бойынша өзгеріп, сейіле бастайды.

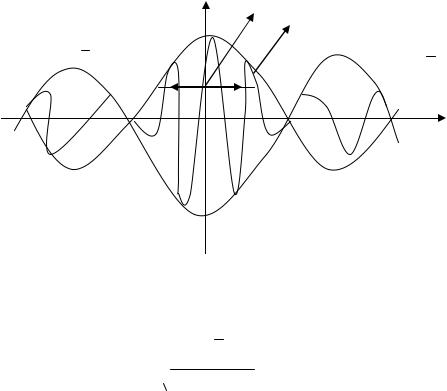
Осы алынған нəтижелерді де Бройль толқындарына қолданайық (2.3 сурет). (2.18)-ші қатынас бойынша толқындық пакеттің жылдамдығы мынаған тең:

	Dξ = Р Dx ~ π
	2H
группалық жылдамдық	фазалық жылдамдық
u = v	U = c
	v

ξ = Р x

-2π

-π

2π

-1

Сурет 2.3. Де Бройль толқындарынан кұрылған толқындық пакеттің кеңістіктегі t уақыт моментіндегі формасы.

υ	=	∂w =	∂Е	(2.26)
		¶k	¶Р

Ал бөлшектің энергиясы E = 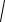p 2 c 2 + m 2 c 4 бұдан

	=	pc2	=	mvc2	= v	(2.27)
v
		E		mc2

яғни де Бройль толқындарынан тұратын толқындық пакеттің топтық жылдамдығы бөлшектің қозғалыс жылдамдығына тең. (2.24) қатынасты түрлендіру нəтижесінде

2π	=	h	,	Dк =	2π p	(2.28)
к					h
		p

мұндай өрнекке келуге болады:

Dp × Dx ³ h

(2.29)

(2.29) теңсіздік кванттық механикада анықталмаған қатынас деп аталады, оны В. Гейзенберг тағайындаған. Бұл қатынас бойынша микробөлшектердің координаталары мен импульстерін нольге тең дəлдікпен анықтау мүмкін емес. Сондықтан кванттық механикада классикалық физиканың негізгі ұғымдарының бірі– материалдық нүктенің траекториясы ұғымы өзінің мағынасын жояды. Мысалы, атомдағы электронның траекториясының болмауы, оның басқа да динамикалық характеристикаларының жойылуына соқтырады. Бұл тек кванттық объектілерден тұратын жүйелерден логикалық тұйықталған механика кұруға болмайтындығын көрсетеді. Электронның қозғалысын сандық тұрғыдан сипаттау үшін классикалық механика заңдылықтарына бағынатын физикалық объектілер қажет болады. Егер электрон мұндай "классикалық объектімен" əсерлессе, онда бұл объектінің де күйі өзгереді. Бұл өзгерістің түрі мен мөлшері электронның күйіне байланысты болады. Сондықтан кванттық механикада классикалық объектіні — " прибор" деп, ал оның электронмен əсерлесуін "өлшеу" деп атайды. Бірақ мұндай "өлшеу" физик-экспериментатордың өлшеу процесімен бірдей емес екендігін ескерген дұрыс. Кванттық механикада "өлшеу" деп бақылаушыға байланысты емес жəне тəуелсіз жүретін классикалық жəне кванттық объектілердің арасындағы кез келген əсерлесуді айтады. Сонымен, "прибор" деп жұмыс принципі классикалық физика заңдылықтарына бағынатын физикалық объектіні айтамыз.

Енді бөлшектердің толқындық қасиетінің бөлшектердің құрылымымен тікелей қатынасы бар ма, жоқ па соны қарастыралық. Э. Шредингер толқындық қасиет микробөлшектердің құрылымымен тікелей байланысты жəне бөлшектің кеңістікте "қожырауы" - (ΨΨ )-ге тең деген интерпретация ұсынды. Мұндай түсініктің қате екені тағайындалды. Анықталмағандық қатынастан толқындық пакеттің сейілу уақыты

t =	m0	( x)2	(2.30)

	H

теория бойынша өлшемі микробөлшектің радиусына жуық толқындық пакетті кұрастыруға əр уақытта да болады. Бірақ мұндай бөлшек орнықты болмайды. Себебі пакетті құрайтын əрбір монохроматты жазық толқынның фазалық жылдамдығы толқындық санға не импульске тəуелді болады. Сондықтан толқындық пакет уақыт өткен сайын ұлғайып, сейіле бастайды. Егер қарастырылып отырған бөлшек макробөлшек болса, мысалы массасы т = 1 г., мөлшері х = 0,1 см, бұл жағдайда толқындық пакеттің сейілу уақыты t = 1025 с. яғни мұндай толқындық пакет іс жүзінде сейілмейді. Керісінше, бөлшек – электрон болса, m =10-31 г., х = 10 см., онда сейілу уақыты t = 10-26 с. Мұндай толқындық пакет лезде сейіледі, яғни, электрондарды жеке толқындардың жиыны деп қарастыруға болмайды.

Қазіргі уақытта толқындық функцияның М. Борн ұсынған статистикалық интерпретациясы қабылданған. Борн бойынша толқындық функцияның модулінің квадраты

Ψ 2 бөлшектің кеңістіктің əртүрлі нүктелерінде болу ықтималдылығының тығыздығын сипаттайды:

W ~ Ψ 2

Статистикалық интерпретация бойынша толқындық қасиет бөлшектің структурасымен тікелей байланысты емес, сондықтан электрондарды немесе басқа да бөлшектерді нүктелік бөлшек деп қарастыра беруге болады. Толқындық функцияның уақыт бойынша өзгеруі микробөлшектердің кеңістіктің əртүрлі нүктелерінде болу

ықтималдылығының өзгеруін көрсетеді. Ал микробөлшектің кұрылымы Борн интерпретациясында мүлдем қарастырылмайды. Бірақ бұл интерпретация жеке микробөлшектердің қозғалысын түсіндіре алмады.

3 ТАРАУ.

КВАНТТЫҚ МЕХАНИКАНЫҢ НЕГІЗГІ ¦ҒЫМДАРЫ

§1. Еркін қозғалыстағы бөлшектің толқындық функциясы

Классикалық механикада бөлшектің қозғалысы динамикалық айнымалылар деп аталатын координата, импульс сияқты физикалық шамалар арқылы сипатталады. Əрбір уақыт моментінде бұл физикалық шамалар нақты мəндерге ие болады. Сондықтан классикалық механикада бөлшектің қозғалысын сипаттаудың негізгі мақсаты осы динамикалық айнымалылардың уақытқа тəуелділігін тағайындау болып табылады. Ал, кванттық механикада динамикалық айнымалылардың əртүрлі мəндерінің ықтималдылығы мен олардың орта мəндері ғана қарастырылады.

Кванттық механикада атомдық объектілердің қасиеттері толқындық функция немесе күй фунциясы деп аталатын арнайы функциямен сипатталады. Жалпы жағдайда, толқындық функция координаталар мен уақытқа байланысты күрделі функция ψ (x, y, z, t) . Толқындық функция микробөлшектердің қозғалысын сипаттайтын белгілі бір дифференциялық теңдеуді қанағаттандыруы қажет. Бұл тендеу Шредингер теңдеуі деп аталады. Шредингер теңдеуінің кванттық механикадағы орны классикалық физикадағы Ньютон заңдарымен шамалас.

Массасы m0 , импульсі р, энергиясы Е = р2/2m0 релятивті микробөлшектің еркін

қозғалысын қарастырайық. Мысал ретінде потенциал айырмашылық U электрондық түтінше арқылы өтетін электрондар ағынының қозғалысын алайық. Бұл электрондардың

Импульсі p = 2m0 e0U

мұнда е0 - электронның заряды, т0 - массасы.

Дэвидсон-Джермер тəжірибелерінің нəтижесінде электрондар ағыны периодтық құрылымды денелермен (кристалдар, фольга) əсерлескенде электрондардың кеңістікте үлестірілуін бақылауға болатындығы тағайындалған еді. Бұл толқындық процесті сипаттайтын толқындардың ұзындығы мен электрондардың қозғалыс жылдамдығы арасындағы байланыс

λ =	h	=	2π	(3.1)
	m0 v		k

Осы тəжірибелік деректерге сүйене	отырып, импульсі			p электронның еркін

қозғалысына де Бройльдің жазық толқындарын сəйкестендіруге болады:

		R			RR		(3.2)
		R			−i( wt −kr )
	Ψ(r , t) = Ae				−i( wt −kr )
мұнда						R
			p 2			R
	E		p 2		R	k
w =		=		,	p =		(3.3)
w =		=		,	p =		(3.3)
	H		2m0 H			H

Сонымен белгілі бір энергиясы мен импульсі бар еркін бөлшектің қозғалысы (3.2) формуламен өрнектелетін толқындық функциямен сипатталады.

§2. Кванттық механикадағы суперпозиция принципі

Кванттық механиканың негізгі ұғымдарының бірі – күйлерді суперпозициялау принципі. Қысқаша түрде бұл қағида мынадай екі тұжырымнан тұрады:

1. Егер система Ψ1 жəне Ψ2 толқындық функцияларымен сипатталатын кванттық

күйлерде болса, онда система осы функциялардың сызықтық түрлендіруі болатын мынадай күйде де бола алады

Ψ = a1Ψ1 + a2 Ψ2

(3.4)

a1 , a2 — уақытқа тəуелсіз, кез келген комплекс сандар.

2. Егер бір күйді сипаттайтын толқындық функцияны кез келген, нольге тең емес комплекс санға көбейтсек, жаңа алынған В функция да сол күйді сипаттайды.

Күйлердің суперпозициялық қағидасы орындалуы үшін толқындық функциялар қанағаттандыратын Шредингер теңдеулері сызықтық теңдеулер болуы қажет. Жалпы жағдайда, жүйе бірінен бірі айырмашылығы аз физикалық шамалармен сипатталатын күйлерден тұрьш, олар Ψ1 , Ψ2 , Ψ3 - толқындық функциялармен өрнектелсе, кванттық

суперпозиция қағидасы бойынша,

Ψ = a1Ψ1 + a2 Ψ2 + a3 Ψ3 +... + an Ψn		(3.5)
немесе
n	ai Ψi	(3.6)
Ψ = ∑	ai Ψi	(3.6)
i=1

толқындық функциямен сипатталатын күрделі күйде де болуы қажет. Егер суперпозицияға енетін күйлердің бірінен бірінің айырмашылығы шексіз аз шама болса, (3.6)-шы формуладағы қосындыны интегралға ауыстыру қажет. Мұндай жағдайдың мысалы ретінде Ψ(x, y, z, t ) функциясымен сипатталатын кез келген

толқындық өрісті де Бройль толқындарының суперпозициясы ретінде қарастыруға болатындығын көрсетейік:

		1		R R
		1	−i ( Et − pr )
	Ψp (x, y, z, t )= (2πH)3 / 2		e	H		(3.7)

Кез келген кванттық күйдің толқындық функциясы
	Ψ(x, y, z, t )= ∫	−∞				(3.8)
	Ψ(x, y, z, t )= ∫	∫ ∫ a(px , p y , pz , t )Ψp (x, y, z, t)dpx dp y dpz				(3.8)
мұнда a(px , p y , pz		+∞
мұнда a(px , p y , pz	) мен p(px , p y , pz ) - де Бройль толқындарының амплитудасы жəне
	R
импульсі.
(3.5)-ші қатынас Ψ(x, y, z, t )		функциясын үшінші ретті Фурье қатарына жіктеумен
пара-пар. Бұл тұжырымды дəлелдеу үшін мынадай белгілеу
	ϕ(px , p y , pz , t )= a(px , p y , pz , t )e−i				Et	(3.9)
	ϕ(px , p y , pz , t )= a(px , p y , pz , t )e−i				H	(3.9)

Сонда (3.7)-ші өрнектің негізінде (3.8)-ші теңдеуді былай жазуға болады:

-¥	i	px ×x+ py ×y + pz ×z	dpx dp y dpz	(3.10)
-¥	i		dpx dp y dpz
Y(x, y, z, t ) = ∫ ∫ ∫ ϕ (px , p y , pz , t )e		H
+¥			(2πH)3 / 2

Сонымен, кванттық суперпозиция принципі бойынша кезкелген күйді де Бройль

толқындарының импульсі R( ) бөлшек күйлерінің суперпозициясы ретінде p px , py , pz

қарастыруға болады.

§ 3. Микробөлшектердің кеңістіктің əртүрлі нүктелерінде болу ықтималдылығы

Кванттық механикада жүйенің күйін сипаттау үшін Y(x, y, z, t ) толқындық функция берілсін. Осы функцияның модулінің квадраты

Y(x, y, z, t )Y* (x, y, z, t ) =		Y		2	(3.11)

бөлшектің кеңістіктің белгілі бір бөлігінде болу ықтималдылығына пропорционал

болады. Ал, бөлшекті q1 , q2 ,...qn нүктесінің төңірегінде						dϑ = dq1 × dq2 ,...dqn кішкене
көлемде табу ықтималдылығы:					2 dϑ
dW = Y* × Ydq × dq	,...dq	n	=	Y		(3.12)
dW = Y* × Ydq × dq	,...dq		=	Y		(3.12)
1 2

Жеке жағдайда, бір бөлшек үшін декарт координаталар жүйесінде (3.12)-ші қатынасты былай жазуға болады:


dW = Y* (x, y, z)× Y(x, y, z)dxdydz =	Y(x, y, z)	2 dxdydz			(3.13)

Кванттық механиканың негізгі ерекшілігі – жүйенің күйі комплексті толқындық
функциямен сипатталады жəне оның модулінің квадраты			Y	2	= Y × Y* бөлшектердің

кеңістіктің белгілі бір бөлігінде болу ықтималдылығының тығыздығына тең болады. Бұл тұжырымнан мынадай екі салдар шығады: біріншіден, Ψ − функцияны кез келген l фазалық көбейткішке көбейткеннен бөлшектердің кеңістікте болу ықтималдылық тығыздығы:

dw =		Y		2	(3.14)

жəне толқындық функция сипаттайтын физикалық шаманың мағынасы өзгермейді. Мұнда l − кез келген нақты сан. Екіншіден, микробөлшекті кез келген V-көлемде табу ықтималдылығы (3.14)- ші формула бойынша

W = ∫ dw = ∫	Ψ	2 dv	(3.15)

γ

Егер соңғы өрнектегі интеграл бүкіл кеңістік бойынша алынса, онда ықтималдылық анықтыққа ауысады, бөлшек кеңістікте қалай да табылады. Сондықтан, Ψ − функцияны бірге нормалай аламыз:

+¥	Ψ	2	dv = 1	(3.16)
+¥		2
∫
-¥

Сонымен, толқындық функция нормалануы қажет, яғни оның модулінің квадраты интегралдануы керек. Бұл шарт толқындық функцияның шексіздікте өте тез кемитін (өшетін) функция болуы керек екендігін талап етеді.

4 ТАРАУ.

КВАНТТЫҚ МЕХАНИКАНЫҢ МАТЕМАТИКАЛЫҚ АППАРАТЫ

§1. Физикалық шамаларды сызықтық, өзара түйіндес операторлармен сипаттау

Кванттық механиканың математикалық аппаратының негізіне – кванттық жүйе координаталарға тəуелді Ψ(x, y, z, t ) функциясымен сипаттальш, осы функцияның

модулінің квадраты координаталар мəндерінің кеңістікте үлестірілуінің ықтималдылығын көрсетеді деген тұжырым жатыр.

Көптеген тəжірибелер кейбір физикалық шамалардың белгілі бір жағдайларда үзілісті мəндерге ие болатынын көрсетеді. Классикалық физикада мұндай жағдай белгісіз еді. Сондықтан классикалық физикада физикалық шамалар үзіліссіз, дифференциалданатын функциялармен сипатталады. Ал кванттық механикада физикалық шамалар үзіліссіз де, дискретті де мəндерге ие болуы мүмкін. Мысалы: бос электрондардың координатасы, импульсі үзіліссіз мəндерге, ал атомдардағы электронның энергиясы Е мен импульс моменті М дискретті мəндерге ие болады.

Мысалы, Бор теориясы бойынша сутегі атомындағы электронның энергиясының мəндері үзілісті:

E = −	m0 Z 2 e04	, n = 1,2,3...	(4.1)
	2H 2 n 2

Үзіліссіз, дифференциалданатын функциялармен дискретті мəндерге ие болатын физикалық шамаларды сипаттау мүмкін емес. 1925 жылы алдымен Гейзенберг, кейін Дирак кванттық механикадағы физикалық шамалардың математикалық көрінісі ретінде функцияларды емес, операторларды пайдалану керек екендігін тағайындады.

Математикада функция деп белгілі бір нақты сандарға басқа бір сандарды сəйкестендіруді айтады. Ал, операторлар деп белгілі бір функцияларға басқа белгілі функцияларды сəйкестендіруді айтамыз.

			ˆ				(4.2)
Мысалы: L =	∂x		LU (x) = v(x)			онда v(x) = 2x,1/ x, e	(4.2)
Мысалы: L =	∂x	,	U (x) = x	, ln x, e	,	онда v(x) = 2x,1/ x, e
ˆ	∂		2	x			x

Классикалық механикада қозғалыстың үзіліссіз болуына байланысты пайдаланылатын функциялар белгілі бір талаптарға сəйкес болу керек. Үзіліссіз, дифференциалданатын, шектелген жөне модулінің квадраты интегралданатын функцияларды регуляр функциялар деп атайды. Осы сияқты кванттық механикадаға операторлар да белгілі бір талапқа жауап беруі кажет. Кванттық механикада күйлерді суперпозициялау кағидасы бұзылмауы үшін тек сызықтық жөне өзара түйіндес

операторлар ғана пайдаланылады. Оператор ˆ сызықтық деп аталады, егер төмендегі

шарт орындалса:

Оператор

Мысалы ˆ

ˆ	(x) + C2U 2	ˆ	ˆ	(x)	(4.3)
L[C1U1		(x)] = C1 LU1	(x) + C2 LU 2

ˆ өзара түйіндес деп аталады, егер мынандай теңдік орындалса

∫ U	*	ˆ	(x)dx =∫ U 2	ˆ*	*	(x)dx	(4.4)
	1	(x)LU 2		(x)L U	1

= −iH ∂ операторының өзара түйіндес оператор екендігін дəлелдейік:

∂x

+∞	*		¶U 2		*			¶U1* (x)	+∞	ˆ * *
+∞	*		¶U 2		*			¶U1* (x)	+∞	ˆ * *
- iH ∫ U	1	(x)		dx = -iHU	1	(x)U 2 (x)	+ ¥ + iH∫ U 2 (x)	dx =	∫ U	2 (x)Px U 1(x)dx
−∞			¶x					¶x	−∞

мұнда U1*U 2 ± ¥ = 0 .

Сызықтық жəне түйіндес операторлар эрмиттік операторлар деп аталады.

L операторының өзара түйіндестігін сипаттайтын (4.4)-ші функционалдық
ˆ
теңдеуді қысқаша мынадай түрде жазуға болады:
					ˆ	ˆ*			(4.5)
					L = L				(4.5)
Сызықтық операторлардың негізгі қасиеттері:
1.	C операторы	A жəне B операторларының қосындысы деп аталады, егер
	ˆ	ˆ	ˆ
мынадай қатынас орындалса:
			ˆ	ˆ	ˆ	ˆ	ˆ	ˆ	(4.6)
			СY = AY + BY,			C	= A + B		(4.6)
2.	С операторы А жəне В операторларының көбейтіндісі болады, егер
				ˆ	ˆ ˆ				(4.7)
				СY = A(BY)					(4.7)

шарты орындалса.

Операторларды қосуға, көбейтуге, тағы басқа амалдарды қолдануға болады, бірақ олардың орындарын ауыстыруға болмайды. Ψ-толқындық функциясымен сипатталатын кванттық күйдегі физикалық шама L-дің орта мəні кванттық механикада мынадай қатынас бойынша анықталынады:

L = ∫ Y

(4.8)

(x)LY(x)dx

Мұнда L - физикалық шама L – ге сəйкес келетін сызықтық, өзара түйіндес оператор.

(4.8)-ші теңдеудің комплекс түйіндесін анықталық:

= ∫ Y

(x)dx

(4.9)

(x)L Y

(4.8)-ші жəне (4.9)-шы теңдеулерді (4.4) – ші теңдеуімен салыстырсақ:

(4.10)

Яғни, кванттық механикада физикалық шаманың орта мəні əр уақытта да нақты

болады. Сонымен кванттық механикада					барлық физикалық	шамаларға сызықтық
(суперпозиция қағидасы сақталуы үшін) жəне өзара түйіндес						(физикалық шаманың
орта мəні нақты болуы қажет) операторлар сəйкестендіріледі.
Физикалық шаманың орта		мəні			жайындағы қосымша		деректерді орташа
						ˆ	ˆ

квадраттық ауытқу деп аталатын шама арқылы да алуға болады: DL = L - L
	2	= ∫ Y			ˆ 2		(4.11)

(DL)				(x)(DL) Y¢(x)dx
					³ 0		(4.12)
			DL2

осы

(4.12) теңсіздікті дəлелделік.

(4.11) теңдеуге сызықтық операторлардың өзара түйіндестік қасиетін

пайдалансақ:

= ∫ Y

³ 0

(x)(DLY(x))dx = ∫

(DLY(x)) dx

енді

қарастырылып

отырған

физикалық

шама

бір ғана

мəнге ие болсын, онда

ˆ ˆ

немесе,

L = L, DL = L - L = 0,

L = 0,

DLY = 0

(L - L)Y = 0 бұдан

(4.13)

LY(x) = LY(x)

Кванттық механикада көбінесе L операторы дифференциалдық оператор түрінде берілетін болғандықтан (4.13) теңдеу операторына сəйкес келетін меншікті мəндерді анықтауға мүмкіндік беретін дифференциалдық теңдеу болып табылады. Ал,

дифференциалдық теңдеулердің шешуі L операторының кез келген мəндерінде бола бермейді. (4.13)-ші дифференциалдық теңдеудің шешуі болатын мəндер: L1, L2, L3,... L- операторының меншікті мəндері деп, ал оларға сəйкес келетін теңдеудің шешулері: Ψ1, Ψ2, Ψ3,...– меншікті функциялар деп аталады. Мысал ретінде екі жағынан бекітілген сымның тербелісін қарастыралық. Тербеліс теңдеуі:

∂2U (x)+ K 2U (x)= 0

∂x 2

U (x) = 0, егер x=0 жəне x=1 болса, осы қатынасты (4.3) теңдеумен салыстырсақ:

∂x 2

−оператор:

меншікті функциялар. Ln

= K

π 2 n 2

− операторының

меншікті

L = −

∂x 2

l 2

мəндері.

Ln : π 2

4π 2

9π 2

,...егер n=1,2,3,…

болса

Ψn

: sin π x, sin

2π

x, sin

3π

x,...

меншікті

l 2

функциялары.

Оператордың меншікті мəндерінің жиыны спектр деп аталады.

Егер оператор

дискретті меншікті мəндерге ие болса,

онда оның

спектрі дискретті болады. Ал,

оператордың меншікті мəндері үзіліссіз болса, онда оның спектрі де біртұтас немесе үзіліссіз болғаны. Кейбір операторлар кей жағдайда дискретті, кей жағдайда үзіліссіз

меншікті мəндерге де ие болуы мүмкін.	L, M операторлары коммутативті деп аталады,
	ˆ	ˆ
егер төмендегі қатынас орындалса
ˆ	ˆ	ˆ ˆ ˆ ˆ	(4.14)
[L, M ]= LM − ML = 0			(4.14)

р физикалық шамалар L жəне М бір мезгілде нақты мəндерге ие болса, онда олардың

операторлары коммутативті болады. Егер осы екі ˆ жəне ˆ операторлар

L M

коммутативті болса, оларға ортақ меншікті функция пайдалануға болады

ΨL = ΨM = ΨLM

(4.15)

Сонымен, оператордың коммутативтілігі физикалық шамалардың бір мезгілде өлшенетіндіктерінің керекті жəне жеткілікті шарты болып табылады.

Теорема: Ψm , Ψn меншікті функциялары өзара ортогоналды болады, егер

	Ψm* Ψn dx = 0			(4.16)
қатынас орындалса.	LΨn	= Ln Ψn
Дəлелделік:	LΨn	= Ln Ψn
	ˆ	= Lm Ψm
	L Ψm	= Lm Ψm
	ˆ*	*
жоғары теңдікті сол жағынан	Ψm * − функциясына, ал төменгі теңдікті дəл солай Ψn −
функциясына көбейтіп, екі теңдікті бірінен бірін алып, интегралдасақ:
* ˆ	ˆ	*	*	(4.17)
∫ Ψm LΨn dx −∫ Ψn LΨm dx = (Lm			− Ln )∫ Ψm Ψn dx	(4.17)

(4.17)-ші теңдеудің сол жағын (4.4) қатынасымен салыстыралық, сонда (4.17)-ші теңдеудің сол жағы нольге тең, демек

(Lm − Ln )∫ Ψm* Ψn dx = 0

егер m ¹ n болса, ∫ Ym* Yn dx = 0

(4.18)

ал, егер т = п болса (4.17)-ші қатынастан ∫ Ym* Yn dx = 1 бұл толқындық функцияларды нормалау шарты. (4.16) жəне (4.18) қатынастарды біріктіріп жазуға болады:

			∫ Ym* Yn dx = δmn						(4.19)
(4.19) меншікті функциялардың ортонормалдық шарты деп аталады.
Мұнда:					m ¹ n
				егер
			0	егер					(4.20)
			δmn	егер	m = n				(4.20)
δmn - Кронекер белгісі.			1	егер	m = n
δmn - Кронекер белгісі.
ˆ	ˆ
L жəне	M операторлар өзара түйіндес операторлар болсын, яғни олар үшін (4.4)-ші
шарт орындалсын. Енді осы			операторлардың						ˆ
шарт орындалсын. Енді осы			операторлардың			көбейтіндісін қарастырайық: L -
операторы өзара түйіндес болғандықтан
		*	ˆ ˆ		ˆ	ˆ*	*
		∫U1 (x)LMU 2 (x)dx =∫ (MU 2 )(x)L U					1 (x)dx
ˆ
Ал M операторының өзара түйіндестігінен:
	ˆ	ˆ* *	ˆ* *	ˆ	2 )dx =∫U		ˆ * ˆ* *		(x)dx
	∫ (MU	2 )L U1 dx =∫ (L U1		)(MU	2 )dx =∫U	2 (x)M L U1			(x)dx
Бұдан			ˆ ˆ		ˆ * ˆ*
		*	ˆ ˆ		ˆ * ˆ*			*
		∫U1	(x)LMU 2 (x)dx =∫U 2 (x)M L U					1 (x)dx

Демек, екі өзара түйіндес операторлардың көбейтіндісі де өзара түйіндес оператор болуы үшін бұл операторлар коммутативті болуы қажет.

§2. Негізгі физикалық шамалардың операторлары

Динамиканың айнымалыларды сипаттайтын операторлар сызықтық жəне өзара түйіндес операторлар болуы қажет. ψ * (x) × Y(x) - шамасы бөлшектің кеңістіктің х- нүктесінде болу ықтималдылығын көрсетеді. Сонда, координатаның орта шамасы

x = ∫ Y* (x)xˆ Y(x)dx (4.21)

(4.8)-ші қатынасты (4.21) теңдікпен салыстырсақ, х координата операторының кез келген f (x) функциясына əсері осы функцияны х − қа көбейткенмен бірдей:

	ˆ
	Xf (x) = Xf (x)
демек бұдан х шамасының операторы осы координатаның өзіне тең болғаны
		X = X
Координата		ˆ		(4.22)
Координата	X = X ,Y = Y , Z = Z			(4.22)
	ˆ	ˆ	ˆ

координаталардың операторлары сол шамалардың өзіне тең болады. Сонда, тек

координаталарға байланысты функция ˆ = - потенциялық энергия

U (x, y, z) U (x, y, z)

операторы. Импульстің операторын анықтау үшін, де Бройль болжамы бойынша Р

импульсі бар микробөлшекке толқындық саны K =	P	жəне жиілігі w =	E	жазық

	H		H

толқын сəйкестендірілетіндігін пайдаланайық. Ал, импульстің меншікті мəндерін анықтайтын

ˆ Y = Y (4.23)

Px Px

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.20151.6 Mб14каз яз ргр №2.docx
#
01.05.201563.47 Кб26каз яз.docx
#
01.05.20151.04 Mб141Казахский язык.pdf
#
01.05.201546.33 Кб12карамель.docx
#
01.05.2015687.36 Кб18Квантовая+физика.pdf
#
01.05.20151.3 Mб44Кванттык механикагакириспе.pdf
#
01.05.201571.76 Кб49Кедейшілік жне оны белгілері.docx
#
10.03.2016168.96 Кб1КИБ-Б416-5В100200-ru-150702-Зуева Е.А. Информатика.doc
#
01.05.2015214.02 Кб30Коллоквиум Квантовая.doc
#
01.05.2015145.92 Кб51Коллоквиум Колебания.doc
#
10.03.201670.81 Кб47КОЛЛОКВИУМ.docx