Конспект лекций по алгебре
.pdf
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
|
Идентификационный |
|
Контрольный экземпляр |
Лист |
|
|
номер: |
|
находится на кафедре |
стр. 61 из 172 |
Дегтярева Н.Е. |
|
|
|
Алгебры, геометрии и |
|
|
|
|
|
анализа |
|
Неполные уравнения прямой |
|
|
|
||
Если |
Ax By C 0 и |
A 0, B 0, C 0, то |
уравнение |
||
называется полным, рассмотрим неполные уравнения прямой. |
|
||||
С 0, следовательно, прямая имеет вид: Ax By 0, т.е. прямая проходит через начало координат;
B 0, следовательно, прямая имеет вид: Ax C 0. Откуда
x C т.е. получили прямую параллельную оси OY : x a;
A
A 0, следовательно, прямая имеет вид: By C 0, Откуда
y C т.е. получили прямую параллельную оси OX : y b;
B
A 0, |
C 0, следовательно, прямая имеет вид: |
определяет ось OX ;
B 0, |
C 0, следовательно, прямая имеет вид: |
определяет ось OY .
By 0
Ay 0
и
и
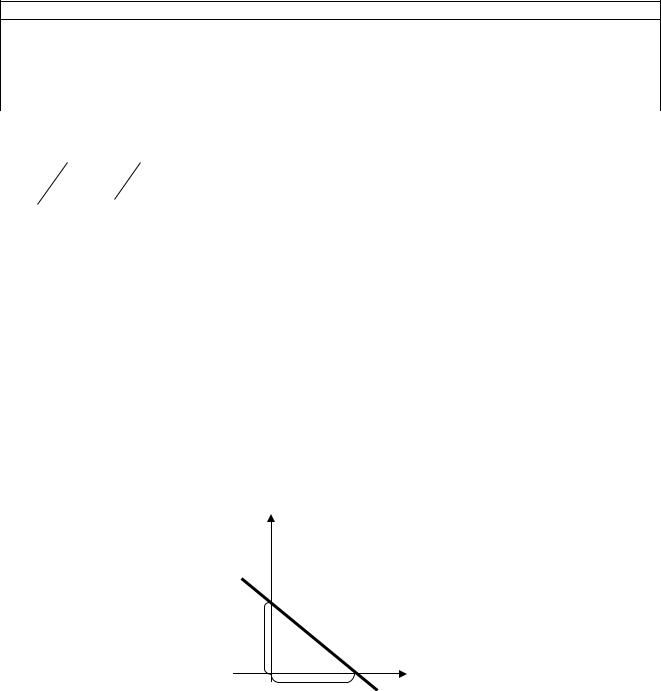
Уравнение прямой в отрезках
Пусть Ax By C 0 – полное уравнение. Перенесем свободный член вправо Ax By С и, в случае если C 0, поделим на него
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 62 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
x |
|
|
|
|
y |
|
1. В сокращенных уравнениях мы уже ввели обозначения |
||||||||||||
_C |
|
|
C |
|
|||||||||||||||
|
|
|
|
B |
|
|
|
|
|
|
|||||||||
|
|
A |
|
|
|
|
|
|
|
||||||||||
a |
C |
, |
|
b |
C |
, тогда получим уравнение в отрезках: |
|
||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
A |
|
|
|
|
B |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
1 |
|
(7.3) |
||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
||||
|
Здесь |
a |
C |
, |
b |
C |
отрезки отсекаемые |
прямой на |
|||||||||||
|
|
B |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
||||
соответствующих координатных осях (рис.7.2)
y
|
|
|
|
b |
|
|
|
|
|
||
|
|
|
|
|
a |
x |
|
|
|
|
|
|
|
|
|
|
|
Рис.7.2 |
|
|
|
|
|
Уравнение прямой с угловым коэффициентом |
|
|
|
|
|||||||
Из общего уравнения Ax By C 0, выразим |
у |
А |
х |
С |
|||||||
В |
В |
||||||||||
|
|
|
|
|
|
|
|
|
|||
Обозначим k |
A |
, |
b |
C |
, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
B |
|
B |
|
|
|
|
|
|||
|
|
|
у kх b |
|
|
|
(7.4) |
||||
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 63 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
где b- отрезок, отсекаемый данной прямой от оси ординат OY , а k -
угловой коэффициент прямой. Уравнение (7.4) называется уравнением прямой с заданным угловым коэффициентом .
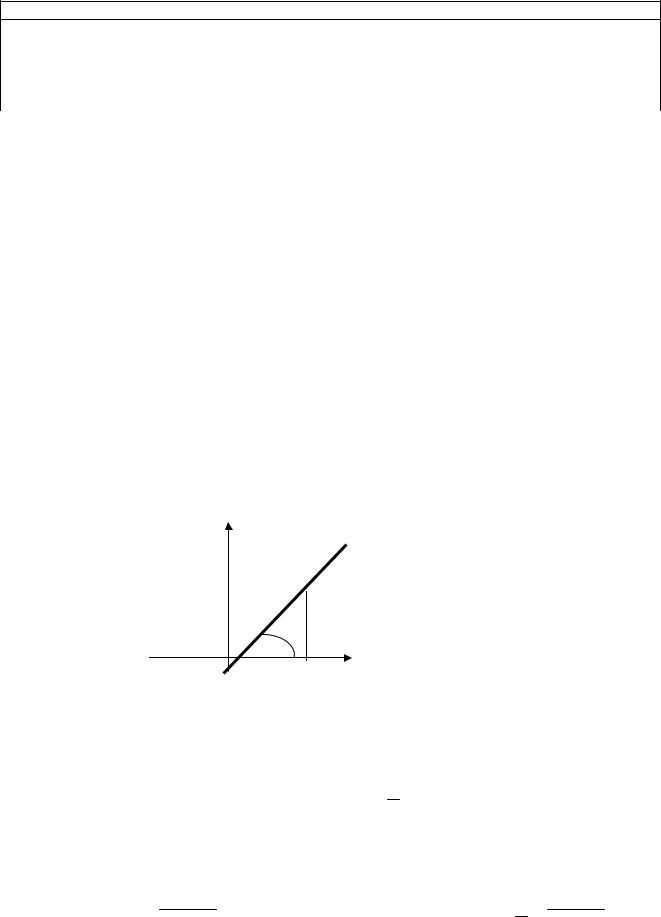
Рассмотрим вектор |
|
(х |
х0, у |
у0), |
не параллельный оси OY . |
|||||
М0М |
||||||||||
из АРМ0 |
(рис. |
7.4) |
имеем tg |
y y0 |
, |
тогда |
||||
|
||||||||||
|
|
|
|
|
|
|
|
x x0 |
|
|
у у0 tg (x x0), |
|
y tg x y0 |
tg x0, |
обозначим |
||||||
tg k, y0 |
tg x0 |
b получим |
у kх b уравнение прямой с |
|||||||
угловым коэффициентом. |
|
|
|
|
|
|
|
|
||
М0(х0,у0)
α
x
А Р
Рис. 5.4
Уравнение прямой через точку и направляющий вектор
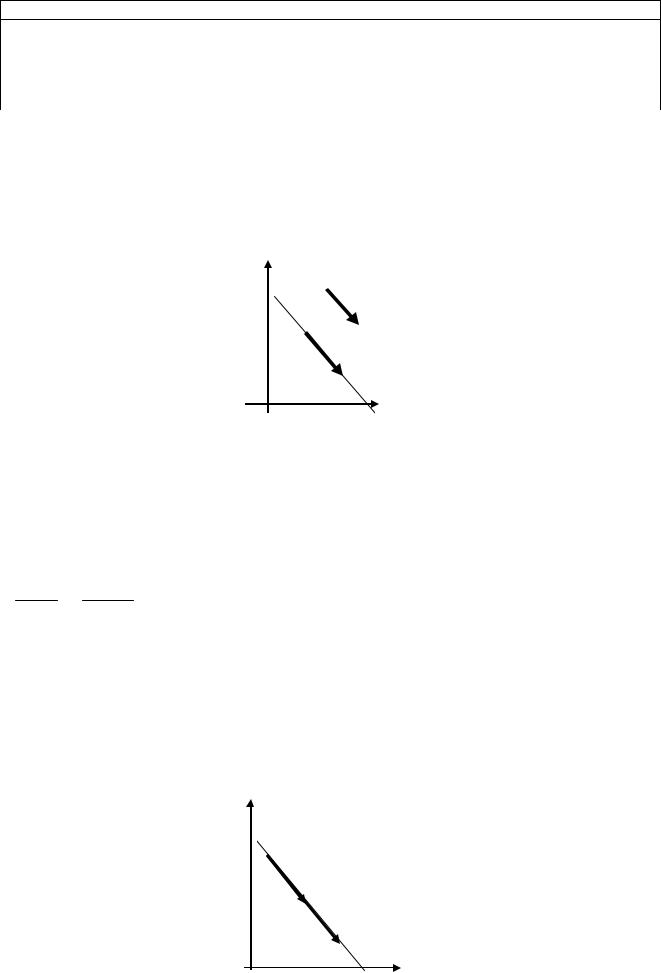
Определение: Всякий ненулевой вектор a || L с координатами (l;m)
параллельный указанной прямой называют направляющим вектором этой прямой (рис. 7.3). Выберем на прямой произвольную точку M(x; y) L и
построим вектор M0M (x x0; y y0). Т.к. векторы a || M0M , то из условия коллинеарности векторов имеем пропорцию:
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
|
Контрольный экземпляр |
Лист |
||||
|
номер: |
|
|
|
находится на кафедре |
стр. 64 из 172 |
||
Дегтярева Н.Е. |
|
|
|
|
|
Алгебры, геометрии и |
|
|
|
|
|
|
|
|
анализа |
|
|
|
|
x x0 |
|
y y0 |
|
|
(7.4) |
|
|
|
|
|
|
|
|||
l m
Которая дает нам каноническое уравнение прямой.
y
а
M0
M
x
Рис.7.3
Уравнение прямой проходящей через две точки
Через любые две несовпадающие точки M1(x1; y1), M2(x2; y2)
можно построить прямую. Пользуясь условием параллельности векторов
M1M и M1M2 (рис.7.4), где M(x; y) L получаем:
x x1 |
|
y y1 |
(7.5) |
|
х2 х1 |
у2 у1 |
|||
|
|
уравнение прямой, проходящей через две точкиМ1 и М2.
y
M1
M
M2
Рис.7.4. x
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 65 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Параметрическое уравнение прямой
Рассмотрим каноническое уравнение прямой (7.4) Оно описывает пропорциональность координат. Введем коэффициент пропорциональности
x x0 y y0 t и распишем два равенства
l m
x x0 tl .
y y0 tm
x x0 tl ,
y y0 tm
(7.6)
Полученное уравнение называется параметрическим уравнением
прямой .
Если t- время, отсчитываемое от некоторого начального момента, то можно считать, что параметрическое уравнение прямой определяет значение движения материальной точки по прямой с постоянной скоростью
v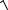 
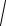l2 m2 .
Уравнение прямой через точку с заданным угловым
коэффициентом
Из канонического уравнения прямой: x x0 y y0 , получаем l m
m
(у у0) l (x x0 ), где отношение координат направляющего вектора
дает угловой коэффициент прямой m k, тогда уравнение l
(у у0) k(x x0) |
(7.7) |
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 66 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Есть уравнение прямой, проходящей через точку M 0(х0, у0) с
заданным угловым коэффициентом k.
Определение: Угловой коэффициент прямой, есть отношение координат нормального или направляющего векторов и равен тангенсу угла наклона прямой относительно положительного направления оси Ox.
Нормированное уравнение прямой
Пусть п- единичная нормаль заданной прямой , т.е. п 1. Возьмем на
прямой произвольную точку M(x; y), координаты ее радиус вектора совпадают с координатами точки. Выразим уравнение прямой L через угол
|
|
|
|
|
|
|
|
|
радиус вектор p |
|
|
|
|
|
|
|
|
|
п |
|
1, то его |
|||
Q ( |
n |
,Ox) |
и |
|
OP |
|
(рис. |
7.5). |
Т.к. |
|
|
|||||||||||||
координатами являются направляющие косинусы |
|
n |
(cosQ;sinQ). |
Т.к. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Q (n,Ox) |
и |
90 Q ( |
n |
, Oy), то cos(90 |
Q) sinQ, |
и |
||||||||||||||||||
следовательно |
n |
(cosQ,sinQ). |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Точка M L, ее проекция на вектор нормали равна радиус вектору |
|||||||||||||||||||||
пр |
|
|
|
р. |
Но, проекцию точки на вектор |
можно вычислить через |
||||||||||||||||||
п |
ОМ |
|||||||||||||||||||||||
скалярное произведение (формула 5.7) пр |
|
|
|
|
|
OM |
n |
. |
Приравнивая |
|||||||
п |
|
ОМ |
||||||||||||||
|
|
|
||||||||||||||
|
|
п |
|
|
1 получим |
|
|
|
n |
|
|
|
|
|||
|
|
|
x cosQ y sinQ p. |
|||||||||||||
правые части и учитывая, что |
|
|
||||||||||||||
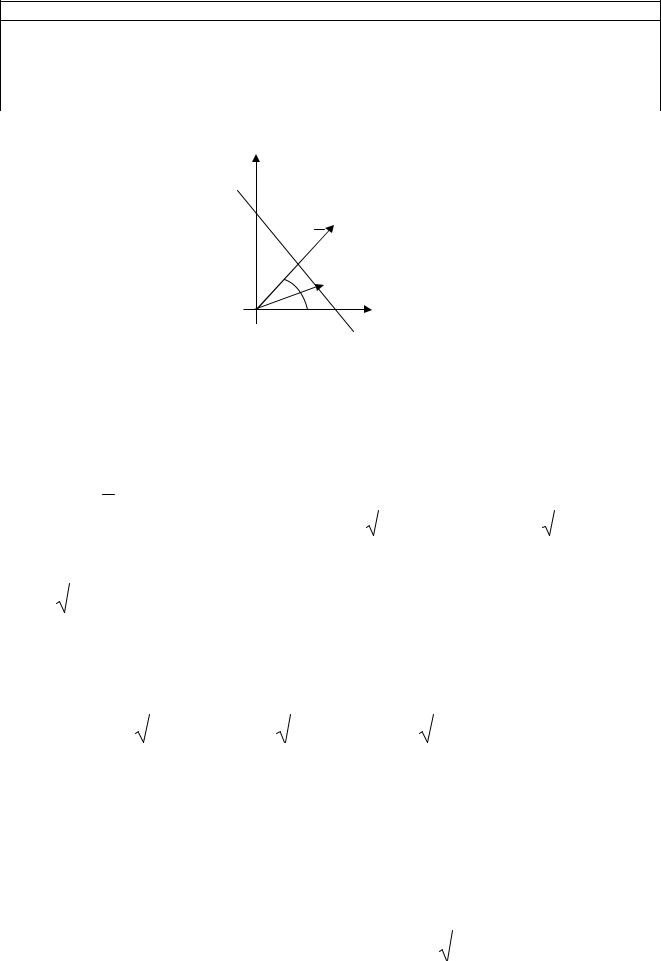
x cosQ y sinQ p 0 |
|
|
|
|
|
|
|
(7.10) |
||||||||
– нормированное уравнение прямой.
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 67 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
у
L
п
Р
QМ
Ох
Рис. 7.5
Установим связь между нормированным и общим уравнением прямой.
|
Если |
|
дано |
L: Ax By C 0, |
то |
At cosQ, |
|
|
Bt sinQ, |
||||||||||||||||||||||||||
tC p. |
|
n |
(A; B), |
поэтому cosQ |
|
|
|
|
|
A |
|
|
, sinQ |
|
|
B |
|
, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 B2 |
|
|
|
|
A2 B2 |
|
|
||||||
p |
|
|
C |
|
|
|
, |
где знак выражения зависит от |
C(противоположный C), |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
A2 B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
следовательно, получается нормированное уравнение |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
х |
|
A |
|
|
|
|
|
у |
|
|
С |
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
A2 B2 |
|
A2 B2 |
|
|
|
|
|
|
|
A2 B2 |
|
|
|
|
|
|
|
|
|||||||||
|
Определение. Совокупность лежащих на данной плоскости |
прямых, |
|||||||||||||||||||||||||||||||||
проходящих через точку M ,называютпучкомпрямыхсцентром вточке M . |
|
|
|||||||||||||||||||||||||||||||||
|
Теорема. |
Если |
A1x B1y C1 |
0 |
и |
|
A2x B2y C2 0 |
||||||||||||||||||||||||||||
уравнения двух различных прямых, пресекающихся в некоторой точке M , |
а |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0, |
|
||||||||||||||||||||||||||
и |
|
произвольные |
числа, |
причем |
|
|
2 2 |
тогда |
|||||||||||||||||||||||||||
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
|
Лист |
|
номер: |
находится на кафедре |
|
стр. 68 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
|
анализа |
|
|
( A1x B1y C1) (A2x B2y C2) 0 есть уравнение |
прямой, |
|||
проходящей через точку M . Более того, какова бы ни была наперед
заданная проходящая через точку M прямая, она определяется выше
записанным уравнением при некоторых и .
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 69 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Лекция 8
Условия параллельности и ортогональности прямых, угол между прямыми, пучок прямых. Уравнения плоскости в пространстве.
Цель: Изучить условия расположения прямых на плоскости, метод вычисления угла между прямыми. Изучить уравнения плоскости в пространстве и основные характеристики.
Расположение прямых на плоскости определяется по взаимному расположению их направляющих векторов или отношением угловых коэффициентов.
1. |
Пусть |
прямые |
заданы |
в |
общем виде. L1: A1x B1y C1 0 и |
||||||||||||||||
|
L2: A2x B2 y C2 |
0, |
где |
n1 (A1; B1), |
n |
2 (A2; B2) |
|||||||||||||||
соответствующие им векторы нормали. |
|
|
|
||||||||||||||||||
|
|
Если L1 || L2, то |
n1 || |
n |
2 |
и |
координаты векторов пропорциональны |
||||||||||||||
|
A1 |
|
B1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A2 |
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Если L1 L2, то |
n1 |
|
n |
2 и значит, скалярное произведение векторов |
|||||||||||||||
равно |
нулю |
n1 |
n |
2 0. |
В |
координатной форме это запишется как |
|||||||||||||||
|
A1A2 B1B2 0. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Если - угол между прямыми |
L1, L2, то он |
равен углу между |
|||||||||||||||||
векторами |
n |
1, |
n |
2 и тогда |
|
|
|
|
|
|
|
|
|
||||||||
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 70 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
cos |
|
n1 |
|
n |
2 |
|
|
|
A1A2 B1B2 |
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n1 |
|
|
|
|
n |
2 |
|
A12 B12 A22 B22 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
2. Пусть прямые заданы каноническим уравнением. L1: x x1 y y1 и l1 m1
L2:x x2 y y2 , где а1 (l1;m1), а2 (l2;m2) соответствующие им l2 m2
направляющие векторы.
Если L1 || L2, |
то |
|
а1 || |
а |
2 |
|
|
и |
их соответствующие координаты |
|||||||||||||||||
пропорциональны |
|
m1 |
|
l1 |
. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
m2 |
l2 |
|
|
|
|
|
|
|
|||||||||
Если L1 L2, |
то |
а1 |
а |
2 |
|
|
и |
их скалярное произведение равно |
||||||||||||||||||
нулю |
а1 |
а |
2 0. В координатной форм |
l1l2 m1m2 0. |
||||||||||||||||||||||
Если - угол |
между прямыми L1, L2 то |
он равен |
углу между |
|||||||||||||||||||||||
векторами |
a1, |
a |
2 |
и тогда |
|
|
|
|
|
|
|
|||||||||||||||
cos |
|
|
l1l2 m1m2 |
|
|
|
. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
l2 |
m2 |
|
l2 m |
2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
|
|
1 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||
3. Пусть уравнения |
прямых |
|
заданы через |
угловой |
коэффициент. |
|||||||||||||||||||||
L1: у k1х b1 и |
L2: у k2х b2 (или в виде (7.7)). Тогда угол между |
|||||||||||||||||||||||||
прямыми, определяется как разность углов наклона прямых к
положительному направлению оси Ox: 1 |
2 подставляя это в |
формулу тангенса разности, получим: |
|