
Конспект лекций по алгебре
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего профессионального образования
«Дальневосточный федеральный университет»
(ДВФУ)
<ШКОЛА ЕСТЕСТВЕННЫХ НАУК>
КОНСПЕКТЫ ЛЕКЦИЙ
Аналитическая геометрия и алгебра
160100.65 – Самолето и вертолето строение
г. Владивосток
2012

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 2 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Лекция 1
Конечные суммы и их свойства. Вычисление определителя
2 2 и 3 3. Системы координат: декартовая, полярная.
Цель: Изучить понятие конечной суммы и ее свойства,
понятие определителя и простейшие методы его вычисления. Знать декартовую и полярную системы координат.
В математике часто рассматривают суммы большого числа слагаемых которые имеют один и тот же вид, но различаются индексами. Для них используют символ суммы (от латинского слова umma). Под символом суммы ставится «индекс суммирования» (любая буква) и значение от которого наш индекс изменяется (некоторое целое число) сверху над символом ставится значение, до которого данный символ изменяется – это пределы суммирования. После символа суммы ставится суммируемое выражение.
n
Определение. Символ , после которого стоит некоторое k 1
выражение, содержащее индекс k, обозначает сумму этих выражений для всех значений индекса k от 1 до n (n N) и называется конечной суммой
n
и записывается ak или |
ak . |
k 1 |
1 k n |

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 3 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Здесь символ k - индекс суммирования, интервал (1,...,n) - интервал
суммирования, ak - суммируемое выражение.
Очевидно, что вместо k может быть взята любая другая буква, т.е.
n |
n |
|
Pk |
PS . Если |
n 0 или n 0, то значение суммы равно нулю. |
k 1 |
S 1 |
|
Примеры:
5
1) ak a1 a2 a3 a4 a5;
k 1
3
2) j j 1 1 2 2 3 3
j 1
Замечание. Иногда вместо 1 k n пишут k(i), тогда символ
ai означает сумму всех таких ai , что целое число i удовлетворяет k(i)
условиям . Если таких целых i нет, сумма считается равной 0. Наконец,
если k(i) включает два или больше условий, это означает, что все условия должны выполняться одновременно.
Свойства конечных сумм
nn
1)Pk Pk ;
k 1 |
k 1 |

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
|
|
Идентификационный |
Контрольный экземпляр |
Лист |
|||
|
|
|
номер: |
|
|
находится на кафедре |
стр. 4 из 172 |
|
Дегтярева Н.Е. |
|
|
|
|
|
Алгебры, геометрии и |
|
|
|
|
|
|
|
|
|
анализа |
|
n |
|
|
|
|
n |
n |
|
|
2) (Pk Qk ) Pk Qk ; |
|
|||||||
k 1 |
|
|
|
|
k 1 |
k 1 |
|
|
n |
m |
|
m |
n |
|
|
|
|
3) Pik Pik , |
|
|
||||||
k 1 i 1 |
|
i 1 k 1 |
|
|
||||
где |
двойная |
сумма |
может быть записана как |
|||||
n |
n |
|
n |
|
|
|
|
|
Pik |
|
Pik ; |
|
|
||||
k 1 i 1 |
|
k,i 1 |
|
|
|
|||
n |
m |
|
|
m |
n |
|
|
|
4) Qk Pi Qk Pi ; |
|
|
||||||
k 1 |
i 1 |
i 1 k 1 |
|
|
||||
n |
|
|
|
n |
aj |
, (замена индекса). Причем i p( j) - взаимно |
||
5) ai |
|
|
||||||
k(i) 1 k(p( j)) |
|
|
|
|||||
однозначная функция. |
|
|
|
|
||||
Иногда требуется записать сумму всех слагаемых кроме одного или двух. Если пропущено слагаемое с номером l, это записывается в виде
ai
k(i) l
Вычисление определителя
Определитель (детерминант) матрицы – это число, (обозначаемое det A, ∆, A, 
 A
A
 ) которое сопоставляется квадратной матрице и может быть вычислено по ее элементам в соответствии со следующими правилами.
) которое сопоставляется квадратной матрице и может быть вычислено по ее элементам в соответствии со следующими правилами.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
|
Идентификационный |
Контрольный экземпляр |
|
Лист |
||||||||||||||
|
|
номер: |
|
|
|
|
|
находится на кафедре |
|
стр. 5 из 172 |
|||||||||
Дегтярева Н.Е. |
|
|
|
|
|
|
|
|
|
|
Алгебры, геометрии и |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
анализа |
|
|
|
|
|||
1) |
Детерминантом |
матрицы |
A a11 |
порядка 1 |
называется |
||||||||||||||
единственный элемент этой матрицы: |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
det A a11 |
|
|
(1.1) |
|||||||||
2) Для матрицы второго порядка мы имеем следующую формулу: |
|||||||||||||||||||
|
|
det A |
|
|
|
a11 |
a12 |
|
|
|
a |
|
a |
22 |
a |
21 |
a |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
a21 |
a22 |
|
|
|
11 |
|
|
12 |
|
|
|||
|
(1.2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из произведения элементов главной диагонали вычитаем произведение элементов побочной диагонали.
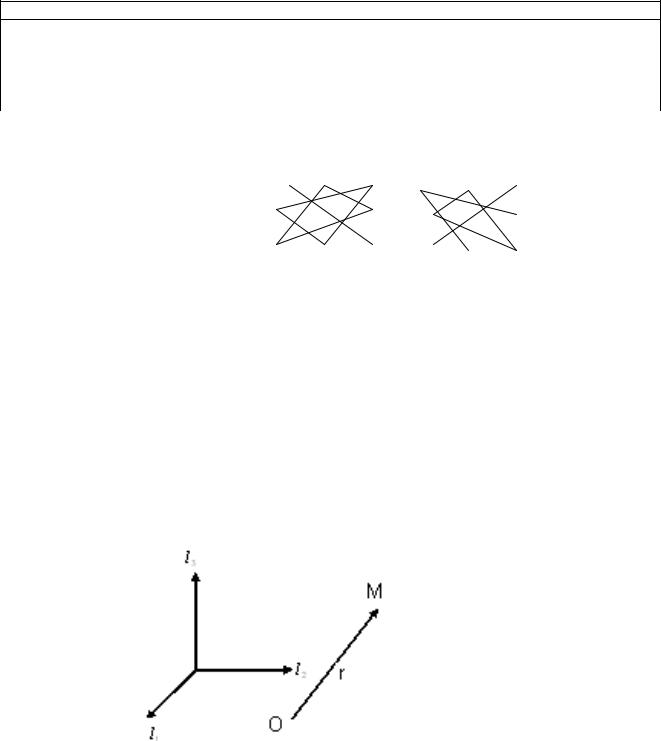
3) Для определителя третьего порядка применяют следующее правило:
1) Правило параллельного переноса.
|
|
|
|
|
|
|
|
|
|
|
a11 |
a12 |
a13 |
a11 |
a12 |
|
|
det A |
|
a21 |
a22 |
a23 |
a21 |
a22 |
|
|
|
|
a31 |
a32 |
a33 |
a31 |
a32 |
|
(1.3) |
а11а22а33 а12а23а31 а21а32а13 а13а22а31 а21а12а33
а11а23а32.
т.е. дописываем первые два столбца определителя матрицы. Далее суммируем произведения элементов главной диагонали и двух параллельных и вычитаем из них произведения элементов побочной диагонали и двух ей параллельных (над верхними элементами диагоналей проставлены соответствующие знаки).
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
|
Контрольный экземпляр |
|
Лист |
|||||||||||||||
|
|
|
номер: |
|
|
|
|
|
|
|
|
находится на кафедре |
|
|
стр. 6 из 172 |
|||||
Дегтярева Н.Е. |
|
|
|
|
|
|
|
|
|
Алгебры, геометрии и |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
анализа |
|
|
|
|
||||
2) Правило треугольника. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
a11 |
a12 |
a13 |
|
|
|
|
|
a11 |
a12 |
a13 |
|
|
|
a11 |
a12 |
a13 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
det A |
|
a21 |
a22 |
a23 |
|
|
|
|
|
a21 |
a22 |
a23 |
|
|
|
a21 |
a22 |
a23 |
|
|
|
|
a31 |
a32 |
a33 |
|
|
|
|
|
a31 |
a32 |
a33 |
|
|
|
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.4) |
|
а11а22а33 а12а23а31 а21а32а13 а13а22а31 а21а12а33
а11а23а32.
Системы координат
1. Декартова система координат.
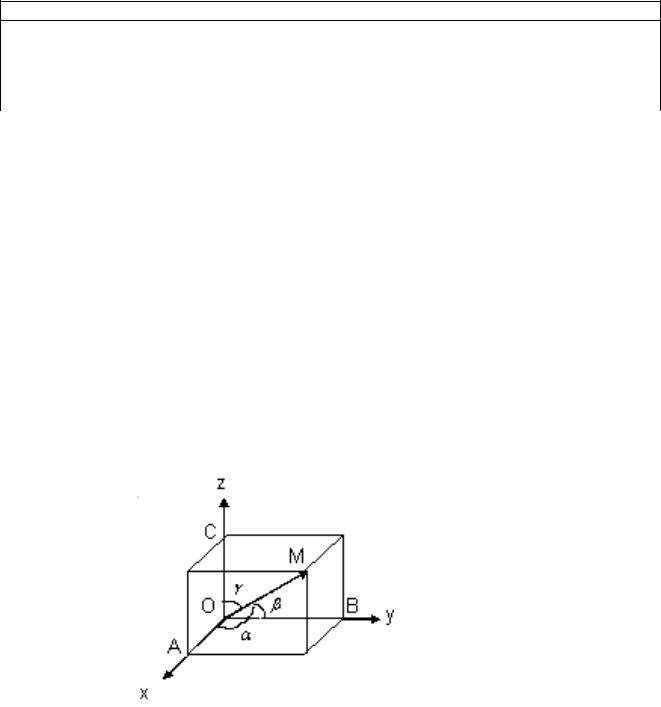
Рис.1.1
Возьмем в пространстве произвольную точку O и рассмотрим некоторую точку М . Соединив эти точки мы получим вектор, который
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 7 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
называется радиус-вектором точки М по отношению к точке O. Если в пространстве выбрать какой-либо базис (рис 1.1), то точке М можно поставить в соответствие упорядоченную тройку чисел – компоненты ее радиус-вектора.
Определение: Декартовой системой координат в пространстве называется совокупность точки и базиса. Итак, рассматриваем три взаимно ортогональные оси в трехмерном пространстве, исходящие из общей точки
O (начала координат и образующие правую тройку).
Рис.1.2.
Оси Ox, Oy, Oz называются осями координат: абсцисса, ордината и аппликата. Плоскости xOy, xOz, yOz называются координатными плоскостями, которые делят все пространство на октаны. Мы рассматриваем радиус-вектор точки М .
Определение: |
Под декартовыми прямоугольными координатами |
x, y, z точки М |
понимаются проекции ее радиус-вектора r на |

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
|
Лист |
||||
|
номер: |
|
|
находится на кафедре |
|
стр. 8 из 172 |
||
Дегтярева Н.Е. |
|
|
|
Алгебры, геометрии и |
|
|
||
|
|
|
|
анализа |
|
|
|
|
соответствующие |
оси |
координат, |
т.е. |
x прОхr OA, |
||||
y прОy r OB, |
z прОzr OC |
(рис.1.2.). |
Для |
краткости их |
||||
просто называют прямоугольными координатами.
Легко видеть, что при заданной системе координат координаты точки определены однозначно. И наоборот, каждая упорядоченная тройка чисел определяет единственным образом точку в пространстве.
Радиус-вектор является диагональю параллелепипеда. Поэтому
r |
x2 y2 z2 |
(1.1) |
Если обозначить через , , углы, образованные радиус-вектором с координатными осями (рис.1.2.), то будем иметь:
x rcos , |
y rcos , |
z rcos |
(1.2)
Эти косинусы называются направляющими косинусами радиус-вектора точки M . Из (2), учитывая (1), получаем важное соотношение:
cos2 cos2 |
cos2 |
x2 |
|
y2 |
|
z2 |
|
|||||||
r2 |
r2 |
r2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
x2 |
y2 z |
2 |
|
r |
2 |
1 |
|
|
|
|
(1.3) |
||
|
r2 |
|
r |
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
т.е. сумма квадратов направляющих косинусов радиус-вектора точки пространства равна единице.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 9 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Из формулы (2) следует, что координата точки М положительна, если радиус-вектор этой точки образует с осью острый угол, и отрицательна, если этот угол тупой.
Измерения x, y, z параллелепипеда равны расстояниям точки М
соответственно от координатных плоскостей Ox, Oy, Oz.
Определение: Декартовые прямоугольные координаты точки М пространства представляют собой расстояния от этой точки до координаты плоскостей, взятые с надлежащим знаком.
Кроме прямоугольной декартовой системы координат используют полярную систему координат. Эта система определена на плоскости, если существует точка O, называемая полюсом и исходящий из этого полюса луч l, который называется полярной осью.
M
r
l
O
Рис.1.3.
В данной системе положение точки фиксируется двумя числами:
радиус-вектором точки r и углом между полярной осью и вектором
OM , т.е. M(r, )

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 10 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Угол называется полярным, отсчитывается от полярной оси в направлении против часовой стрелки. У плюса точки O r 0, а угол не определен. У всех остальных точек r 0 и изменяется в пределах от 0
до 2 , измеряется в радианах.
Если мы поместим полярную систему координат полюсом в начало прямоугольной декартовой системы координат, то декартовы координаты будут выражаться через полярные по формулам:
x rcos , y rsin (1.4)
Полярные координаты через декартовые выражаются соотношениями:
|
|
, |
arctg |
y |
|
|
r |
x2 y2 |
(1.5) |
||||
x |
||||||
|
|
|
|
|
