
Конспект лекций по алгебре
.pdf
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 71 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
tg tg( 1 2) |
|
|
tg 2 tg 1 |
|
(8.1) |
|||
1 tg 2 |
tg 1 |
|||||||
|
|
|||||||
Или через угловые коэффициенты прямых |
|
|||||||
tg |
|
|
k2 k1 |
|
|
|
(8.2) |
|
|
1 k2 k1 |
|||||||
|
|
|
||||||
Из соотношения (7.9) легко определяются условия ортогональности и коллинеарности прямых.
Если L1 || L2, то угол между ними равен нулю 0 и, следовательно
tg 0, что возможно только при обращении в нуль числителя в формуле
(7.9) k1 k2 0 и значит, для параллельных прямых k1 k2.
Если L1 L2, то 90 |
|
|
, |
и следовательно tg не определен, |
|
||||
|
2 |
|
|
|
т.е. знаменатель формулы (7.9) обращается в нуль :1 k2 k1 0. Откуда
получаем условие ортогональности прямых: k1 1.
k2
Расстояние от точки до прямой
Выразим расстояние от произвольной точки на плоскости М0(х0; у0)
до прямой L: Ax By C 0. Пусть нам известны n (A; B) и
М1(x1, y1) лежащая на прямой. Тогда, расстояние от точки до прямой
можно выразить через проекцию d npn M1M0 . И по формуле

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
|
Идентификационный |
|
|
Контрольный экземпляр |
|
Лист |
||||||||||||||||||
|
|
|
|
номер: |
|
|
|
|
|
|
|
|
|
находится на кафедре |
|
стр. 72 из 172 |
|||||||||
Дегтярева Н.Е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Алгебры, геометрии и |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
анализа |
|
|
|
|||
определяем: d |
|
|
A(x0 |
x1) B(y0 |
y1) |
|
|
. |
|
|
|
||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
A2 B2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Раскрывая скобки получим: |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
d |
|
Ax0 By0 С |
|
|
|
|
|
|
|
|
(8..3) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
A2 B2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Если |
дано |
нормированное |
|
|
|
уравнение |
прямой, |
то |
|||||||||||||||
d |
|
cosQ x0 sinQ y0 p |
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Определение. Если в пространстве задана произвольная плоскость и
фиксирована произвольная декартова система координат, то плоскость определяется в этой системе координат уравнением первой степени (и
наоборот: всякое уравнение первой степени с тремя неизвестными x, y, z
определяет плоскость относительно данной системы координат).
Уравнение плоскости проходящей через точку и вектор нормали
Определение: Всякий ненулевой вектор |
|
|
п |
ортогональный |
|||||||||||
плоскости, с координатами (A; B;С), называется нормалью к плоскости. |
|||||||||||||||
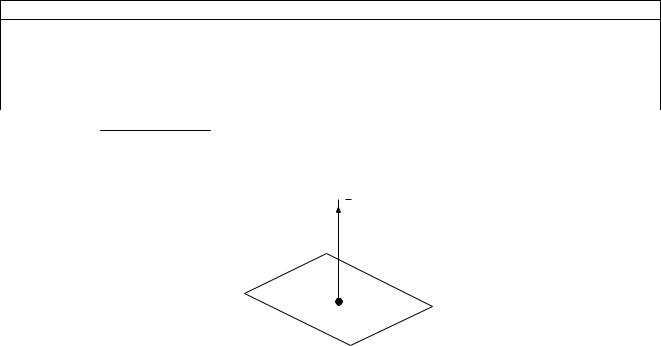
Пусть на плоскости задана некоторая точка |
M(x0; y0; z0) и вектор |
||||||||||||||
нормали |
n |
(A; B;С). Если |
вектор |
n |
, |
то |
n |
ортогонален любой |
|||||||
прямой этой плоскости (рис. 8.1), следовательно, |
|
n |
|
|
|
, |
тогда их |
||||||||
|
M0M |
||||||||||||||
скалярное произведение обращается в ноль |
|
n |
|
|
0. |
Записывая |
|||||||||
|
M0M |
||||||||||||||
последнее равенство в координатной форме получим: |
|
|
|
|
|
|
|
||||||||
|
|
A(x x0) B(y y0) C(z z0) 0 |
(8.4) |
||||||||||||
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 73 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
где 
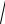 A2 B2 C2 0.
A2 B2 C2 0.
 n(A,B,C)
n(A,B,C)
M0(x0, y0,z0)
Рис. 8.1.
Общее уравнение плоскости
Раскроим скобки в уравнении (8.4) и обозначим константу
Ax0 By0 Cz0 D. Получим уравнение:
Ax By Cz D 0 |
(8.5) |
– общее уравнение плоскости.
Если Ax By Cz D 0 и A1x B1y C1z D1 0
определяют одну и ту же плоскость, то существует действительное число t,
такое, что A tA1, B tB1, C tC1, D tD1.
Неполные уравнения плоскости |
|
Ax By Cz D 0 – называется полным, если |
A, B,C, D 0, |
рассмотрим различные неполные уравнения плоскости: |
|
1) D 0– плоскость проходит через начало координат O(0; 0; 0)
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
|
Идентификационный |
|
Контрольный экземпляр |
|
Лист |
||||
|
|
|
номер: |
|
|
находится на кафедре |
|
стр. 74 из 172 |
||
Дегтярева Н.Е. |
|
|
|
Алгебры, геометрии и |
|
|
|
|||
|
|
|
|
|
|
анализа |
|
|
|
|
2) |
A 0– |
плоскость |
параллельная |
оси |
Ox, |
так |
как |
|||
n |
(0; B;C) Ox; |
|
|
|
|
Oy, |
|
|
||
3) |
B 0– |
плоскость |
параллельная |
оси |
так |
как |
||||
n |
(A; 0;C) Oy; |
|
|
|
|
|
|
|
||
4) |
C 0– |
плоскость |
параллельная |
оси |
Oz, |
так |
как |
|||
n |
(A; B; 0) Oz. |
|
|
|
|
|
|
|
||
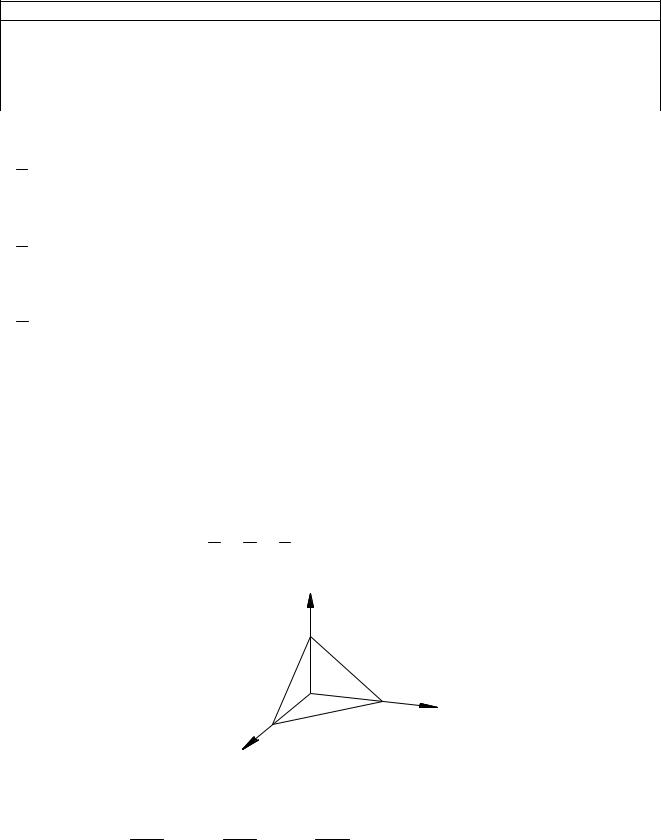
Уравнение плоскости в отрезках
Если дано полное уравнение плоскости Ax By Cz D 0, тогда с помощью преобразований аналогичных уравнению прямой можно получить
уравнение плоскости в отрезках (рис.8.2):
|
x |
y z 1. |
(8.6) |
|
|
a |
b |
c |
|
|
|
|
z |
|
|
|
|
с |
|
|
|
|
b |
y |
|
x |
a |
|
|
|
|
|
|
|
|
|
|
Рис 8.2 |
|
где a D, |
b D, |
c D - |
отрезки, которые отсекает |
|
A |
B |
C |
|
|
плоскость от координатных осей Ох, Оу и Оz соответственно (рис. 8.2),
могут быть меньше нуля.
Уравнение плоскости, проходящей через три различные точки
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
|
Идентификационный |
|
Контрольный экземпляр |
Лист |
||
|
|
номер: |
|
|
находится на кафедре |
стр. 75 из 172 |
|
Дегтярева Н.Е. |
|
|
|
|
Алгебры, геометрии и |
|
|
|
|
|
|
|
анализа |
|
|
Даны |
три |
точки: |
M1(x1; y1; z1), |
M2(x2; y2; z2), |
|||
M3(x3; y3; z3).
Чтобы произвольная точка пространства M(x; y; z) принадлежала плоскости, т.е. M,M1,M2,M3 , необходимо и достаточно, чтобы
M1
M3
M
M2
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8.3 |
|
|
|||
|
векторы |
|
|
|
|
, |
|
были |
компланарны |
(рис. 8.3), |
|||||||
M1M, |
M2M |
M3M |
|||||||||||||||
следовательно, |
смешанное произведение векторов должно равняться нулю |
||||||||||||||||
|
|
|
|
|
|
|
0. Записывая данное равенство в координатной форме |
||||||||||
|
M1M |
M2M |
M3M |
||||||||||||||
получим уравнение плоскости проходящей через три точки: |
|
||||||||||||||||
|
|
|
|
|
x x1 |
|
y y1 |
z z1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x2 x1 |
y2 y1 |
z2 z1 |
|
0 |
|
(8.7) |
|||||||
|
|
|
|
x3 x1 |
y3 y1 |
z3 z1 |
|
|
|
|
|||||||
Уравнение плоскости через точки и направляющие вектора
Определение: Два произвольных неколлинеарных вектора, лежащих в
указанной плоскости или параллельных ей, называются направляющими
векторами данной плоскости.
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 76 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
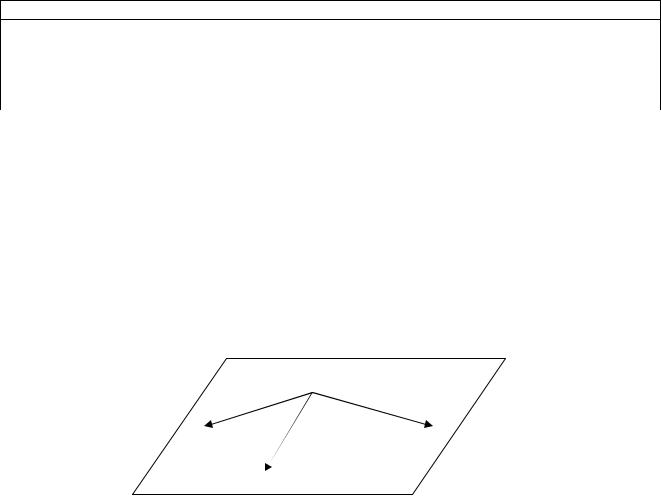
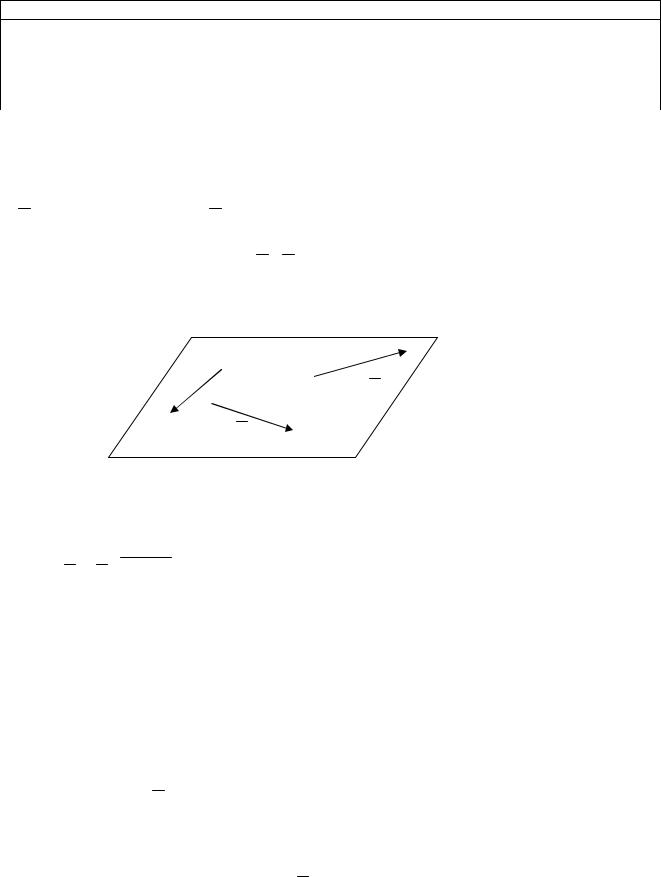
Для того, чтобы записать уравнение плоскости, проходящей через
заданную точку M0(x0; y0; z0) и два направляющих вектора плоскости
p |
(l1; m1; n1), |
q |
(l2; m2; n2) |
воспользуемся |
условием |
|||||
компланарности векторов |
p |
, |
g |
, |
M0M |
(рис.8.4), где |
M(x; y; z) |
|||
произвольна точка пространства принадлежащая плоскости. |
|
|||||||||
M0
g
M p
Рис.8.4
p g M0M 0 или в координатной форме:
|
|
|
|
|
|
x x0 |
y y0 |
z z0 |
|
|
|
|
|
|
|
|
l1 |
m1 |
n1 |
0 |
(8.8) |
|
|
|
|
|
|
l2 |
m2 |
n2 |
|
|
Нормированное уравнение плоскости |
|
|
||||||||
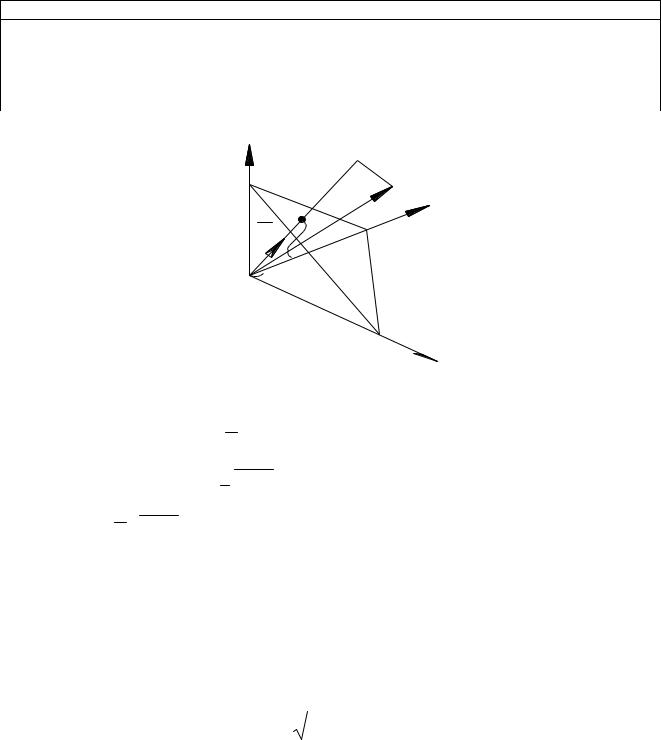
Пусть дана |
|
n |
– единичная нормаль |
и расстояние от точки P до начала |
||||||
координат p |
|
|
|
, выразим уравнение плоскости |
через: p и углы |
|||||
|
OP |
|
||||||||
, , между осями и вектором n (рис. 8.5).
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 77 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
z |
|
Q |
|
|
|
|
|
M |
|
P |
y |
|
|
n
 p
p
 x
x
Рис. 8.5
Координаты вектора n(cos ,cos ,cos ), очевидно M тогда и
только тогда, когда прn OM p, следовательно, должно выполняться
равенство |
n |
OM p, отсюда получаем |
нормированное уравнение |
плоскости cos x cos y cos z p 0. |
|||
Чтобы |
привести полное уравнение |
Ax By Cz D 0 к |
|
нормированному виду, нужно каждый коэффициент уравнения умножить на
нормирующий множитель t |
|
1 |
|
, |
знак |
зависит от D. |
||
|
|
|
||||||
|
|
A2 B2 C2 |
|
|
|
|
||
Знак выбираем противоположный D, т. к. p t D |
|
t |
p |
. |
||||
|
||||||||
|
|
|
|
|
|
|
D |
|
Расстояние от произвольной точки пространства до указанной плоскости определяется аналогично расстоянию от точки до прямой :
d |
cos x0 cos y0 cos z0 p |
(8.9) |

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 78 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Определение. Совокупность всех плоскостей, проходящих через одну и ту же прямую L, называется пучком плоскостей (с центром в L).
Теорема. Если даны две не параллельные плоскости
1 : A1x B1y C1z D1 0, 2 : A2x B2y C2z D2 0 и
1 2 L, а и – какие угодно числа неравные нулю одновременно,
то A1x B1y C1z D1 A2x B2 y C2z D2 0
есть уравнение плоскости, проходящей через прямую L.
Определение. Совокупность всех плоскостей, проходящих через данную точку M0(x0; y0; z0), называется связкой плоскостей (с центром в
M0). |
|
Теорема. Уравнение связки с центром в |
M0(x0; y0; z0) имеет вид |
A(x x0) B(y y0) C(z z0) 0, где |
A, B,C и не равны |
нулю одновременно. |
|
Угол между двумя плоскостями. Условия параллельности
и перпендикулярности плоскостей
Пусть даны |
|
две |
плоскости: 1 : A1x B1y C1z D1 |
0 и |
|||||||||||||||||||
2 : A2x B2y C2z D2 |
|
|
|
|
|
|
|
|
|||||||||||||||
0, где |
( 1, 2) ( |
n1, |
n |
2)- |
угол |
||||||||||||||||||
между |
|
|
|
нормальными |
векторами |
плоскостей, |
тогда |
||||||||||||||||
cos |
|
n1 |
n |
2 |
|
|
|
A1A2 B1B2 C1C2 |
|
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
n1 |
|
|
|
|
n |
2 |
|
A12 B12 C12 |
A22 B22 C22 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
|
|
|
Идентификационный |
|
|
Контрольный экземпляр |
Лист |
||||||||||||||||||||
|
|
|
|
номер: |
|
|
|
|
|
|
|
|
|
находится на кафедре |
|
стр. 79 из 172 |
||||||||||||
Дегтярева Н.Е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Алгебры, геометрии и |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
анализа |
|
|
|
|
|
|
|
|||
Если |
1 |
|| |
2 |
то |
n |
|
|| |
n |
2 |
и |
|
A1 |
|
|
B1 |
|
C1 |
. |
|
|
|
|||||||
|
|
A |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
B |
2 |
|
C |
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если |
1 |
|
2 |
то 90 |
|
и A A |
|
B B |
2 |
C C |
2 |
0. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
1 |
|
1 |
|
|
||||||||||
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 80 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Лекция 9
Уравнение прямой в пространстве. Прямая и плоскость в пространстве,
разные задачи
Цель: изучить уравнения прямой в пространстве и их характеристики,
методы определения взаимного расположения прямой и плоскости.
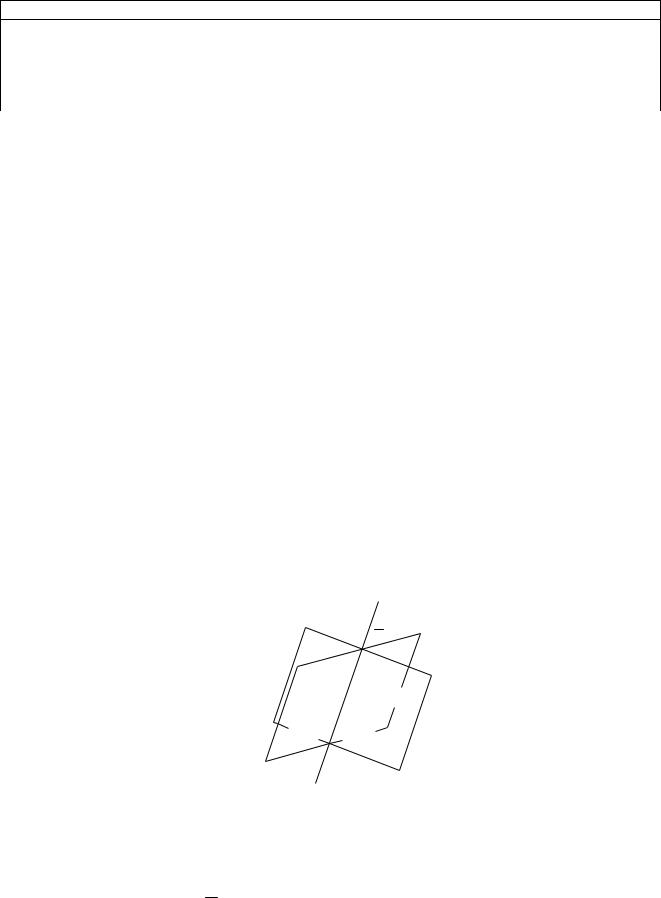
Прямая как пересечение двух плоскостей
Прямую в пространстве можно задать как пересечение двух непараллельных плоскостей 1, 2 (рис.9.1)
|
A x B y C z D 0 |
(9.1) |
|||
L: |
1 |
1 |
1 |
1 |
|
A2x B2 y C2z D2 0 |
|
||||
L
 a
a
1
2
Рис. 9.1
Каноническое уравнение прямой
Ненулевой вектор a параллельный заданной прямой Lбудем называть
направляющим вектором этой прямой (рис. 9.2). Выведем уравнение прямой,
