
Конспект лекций по алгебре
.pdf
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 41 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
a AB (x2 x1; y2 y1; z2 z1), где A(x1; y1; z1),
B(x2; y2; z2) (рис. 5.4).
y
yB |
|
B |
|
A
yA
O |
xA |
xB |
x |
Рис. 5.4
|
|
|
|
|
|
|
|
|
|
|
||
Найдем координаты точки M , которая делит |
AB в отношении |
|||||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||
( , 0). Отношение |
|
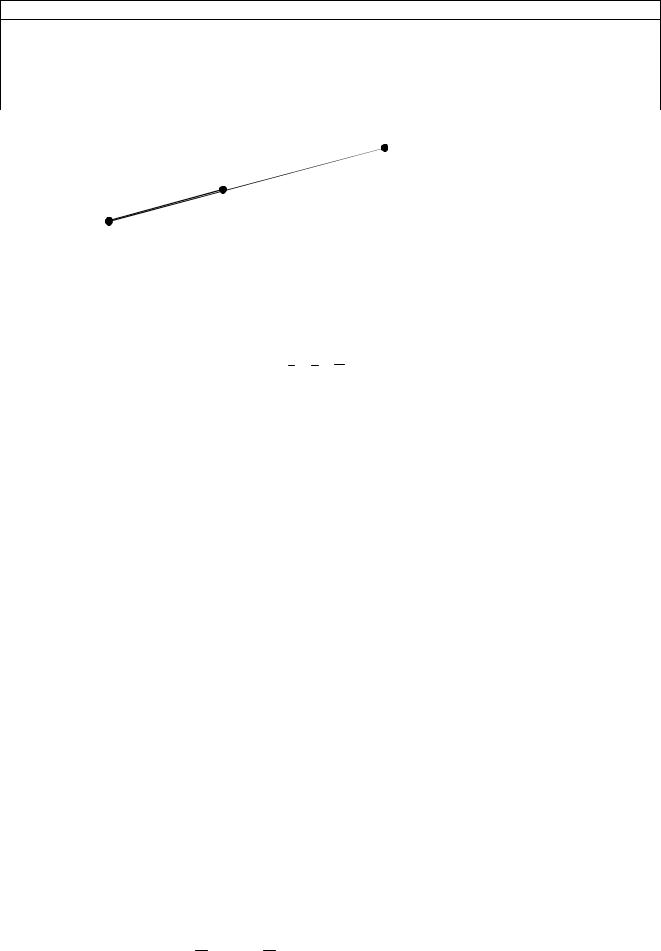
, в котором произвольная точка M x; y; z делит |
||||||||||
|
|
|||||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
отрезок M1M2 (Рис. 5.5) |
|
|
|
|
|
. |
||||||
удовлетворяет равенству |
M1M |
MM2 |
||||||||||
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
|
Идентификационный |
Контрольный экземпляр |
Лист |
|
|
номер: |
находится на кафедре |
стр. 42 из 172 |
Дегтярева Н.Е. |
|
|
Алгебры, геометрии и |
|
|
|
|
анализа |
|
|
|
|
M2 x2; y2;z2 |
|
|
M x; y;z |
|
|
|
M1 x1; y1;z1
Рис.5.5.
Пусть A(x1; y1; z1), B(x2; y2; z2), а M x; y; z , тогда разложим обе части равенства по базису i, j, k , тогда (x x1) (x2 x1),
(y y1) (y2 y1),
(z z1) (z2 z1)
т.к. 0, следовательно
x |
x1 x2 |
,. |
y |
y1 y2 |
, |
z |
z1 z2 |
|
|||||||
|
|
||||||
|
|
|
|
|
|||
(5.1) |
|
|
|
|
|
|
|
Когда M делит отрезок пополам, имеем:
x |
x1 x2 |
, |
y |
y1 y2 |
, |
z |
z1 z2 |
. |
(5.2) |
|
|
||||||||||
|
||||||||||
|
|
|
||||||||
2 |
|
2 |
|
2 |
|
|
||||
Скалярное произведение векторов
Определение. Скалярным произведением двух векторов называется число
(скаляр) равное произведению длин этих векторов на косинус угла между ними:
|
|
|
|
|
|
|
|
|
|
|
a |
b |
a |
|
b |
cos |
(5.3) |
||||
|
|
|
|
|
|
|
|
|
|
|
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 43 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
где - угол между векторами a, b . Обозначают скалярное произведение
как a b (a,b).
Т.к. прbа a cos , то скалярное произведение можно вычислить по
формуле
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
b |
пр |
|
|
а |
или |
|
a |
b |
|
a |
|
|
пр |
|
b |
(5.4) |
|||||||
|
b |
|
|
|
|
|
a |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Физический смысл скалярного произведения: работа постоянной силы при прямолинейном перемещении ее точки приложения. A F s.
Свойства скалярного произведения
1) a b b a (коммутативность).
Непосредственно следует из коммутативности произведения чисел;
2) (a b)c a c b c (дистрибутивность).
Для доказательства этого свойства воспользуемся линейным свойством проекции и формулой, связывающей скалярное произведение и проекцию.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку пр |
|
|
|
( |
а |
b) пр |
|
|
а |
пр |
|
b |
и |
a |
b |
b |
пр |
|
а |
, тогда |
||||||||||||||||||||||
c |
c |
|
c |
b |
||||||||||||||||||||||||||||||||||||||
( |
a |
|
|
) |
c |
|
|
|
c |
|
|
пр |
|
( |
а |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
b |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
с пр c а с пр c b = a c b c;
2)Скалярный квадрат вектора равен квадрату модуля этого
вектора:
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
||||||||
|
номер: |
находится на кафедре |
стр. 44 из 172 |
||||||||
Дегтярева Н.Е. |
|
|
|
|
|
|
|
Алгебры, геометрии и |
|
||
|
|
|
|
|
|
|
|
анализа |
|
||
|
|
a |
|
a |
|
|
|
a |
|
2 |
(5.5) |
|
|
|
|
||||||||
Выполняется для любого вектора a, следует из определения, поскольку угол между вектором a и a равен нулю, тогда cos 1;
4) Скалярный множитель можно выносить за знак скалярного произведения
a ( b) (a b)
где - произвольное действительное число.
|
Доказывается по |
аналогии со |
|
|
свойством 2. |
Поскольку |
||||||||||||||||||
пр |
|
( |
а |
) пр |
|
|
а |
|
|
|
a |
|
|
|
|
|
|
|
|
пр |
|
а |
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
и |
|
b |
b |
тогда |
||||||||||||||||
b |
b |
|
|
|
|
|
|
|
b |
|||||||||||||||
a( b) a прa ( b) a прa (b) (a b);
5)Скалярное произведение равно нулю тогда и только тогда, когда их скалярное произведение равно нулю.
a |
|| b |
a |
b 0 |
(5.6) |
|
|
||||||
Доказательство. Докажем, что если векторы ортогональны, то их |
||||||||||||
|
|
|
|
|
|
a |
и |
|
|
|||
скалярное произведение равно нулю. Действительно, если |
|
b |
||||||||||
ортогональны, следовательно, - угол между векторами |
a |
, |
|
|
равен 90 , |
|||||||
b |
||||||||||||
тогда cos 0, тогда из определения следует, что a b (a,b) 0.
Докажем теперь, что если скалярное произведение векторов a, b равно нулю, то они ортогональны. Пусть оба вектора ненулевые, (т.к. в
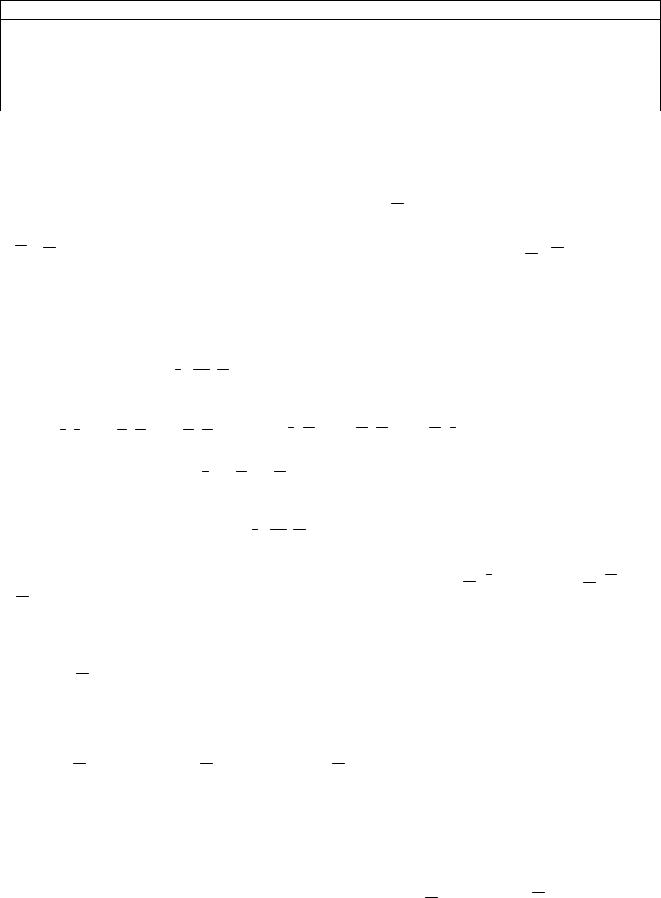
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 45 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
противоположном случае доказательство тривиально, поскольку нулевой вектор не имеет определенного направления и его можно считать
|
|
|
|
|
|
|
ортогональным любому вектору). Тогда |
a |
0 и |
b |
0, поэтому |
||
|
|
|
|
|
|
|
a b 0 только в том случае, если cos 0, т.е. векторы a, b должны быть ортогональны.
6) векторы ортонормированного базиса декартовой прямоугольной
системы координат i, j, k удовлетворяют соотношениям:
(i,i) ( j, j) (k,k) 1, (i, j) ( j,k) (k,i) 0 т.к. векторы
попарно ортогональны i j k .
Если базисные векторы i, j, k ортогональны, то для каждого вектора
|
a |
координаты в данном базисе будут равны: |
1 |
|
( |
a |
,i) |
, |
|
2 |
|
( |
a |
, j) |
, |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
3 |
( |
a |
, |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
2 |
|
|
|
|
|
|
j |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
k |
|
|
|
|
|
|
|
, |
|
|
|
– ортонормированный |
|
|
||||||||||||||||||||||||||||||||||
, |
поскольку |
i |
j, |
k |
|
базис, тогда |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 ( |
a |
, |
|
), |
|
2 ( |
a |
, |
|
), |
|
3 ( |
a |
, |
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
i |
|
j |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Геометрический смысл скалярного произведения: с помощью скалярного
произведения можно вычислить проекцию вектора a на вектор b, и косинус угла между векторами:

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 46 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
|
|
|
|
пр |
|
|
|
а |
|
|
a |
|
|
cos |
|
|
a |
|
|
|
|
a |
|
|
b |
|
a |
|
|
|
b |
|
(5.7) |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
b |
|
|
|
|
|
|
|
(5.8) |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
1 |
|
2 |
|
3 |
|
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
Теорема. Если базис ортонормированный и |
|
i |
j |
k |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
2 |
|
3 |
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
b |
i |
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
1 1 |
2 2 |
3 3 |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
b |
(5.9) |
|
|
|||||||||||||||||||||||||||||||||||||||||||
где a ( 1; 2; 3), b ( 1; 2; 3)– координаты векторов в
ортонормированном базисе.
Доказательство. |
Поскольку |
a |
1i 2 j 3k |
и |
b 1i 2 j 3k, тогда найдем скалярное произведение векторов используя свойства дистрибутивности и ассоциативности:
a b ( 1i 2 j 3k) ( 1i 2 j 3k)=
=1 1i i 1 2i j 1 3i k
2 1 j i 2 2 j j 2 3 j k
3 1k i 3 2k i 3 3k k 1 1 2 2 3 3.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 47 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
|
|
|
|
Следствие. Необходимым и достаточным |
|
условием ортогональности |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
a |
1 |
|
2 |
|
|
3 |
|
|
|
|
|
|
1 |
|
2 |
|
|
3 |
|
|
|
|||||||||||||
векторов |
i |
j |
k |
|
и |
b |
i |
|
j |
k |
является |
|||||||||||||||||||||||||||||
условие 1 1 2 2 3 3 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
Следствие. |
|
|
|
|
Длина |
|
|
|
(модуль) |
|
вектора |
|
|
|
|
a |
|
равна |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
a |
|
( )2 ( |
2 |
)2 ( |
3 |
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Следствие. |
cos |
|
|
|
1 1 2 2 |
3 3 |
|
|
|
|
, где |
- угол |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
2 |
2 |
2 |
2 |
2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
3 |
|
|
|
1 |
2 |
|
|
|
3 |
|
|
|
|
|
|||
между векторами a, b .
Следствие. Если A(x1; y1; z1), B(x2; y2; z2), тогда:
AB 
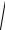 (x2 x1)2 (y2 y1)2 (z2 z1)2 .
(x2 x1)2 (y2 y1)2 (z2 z1)2 .
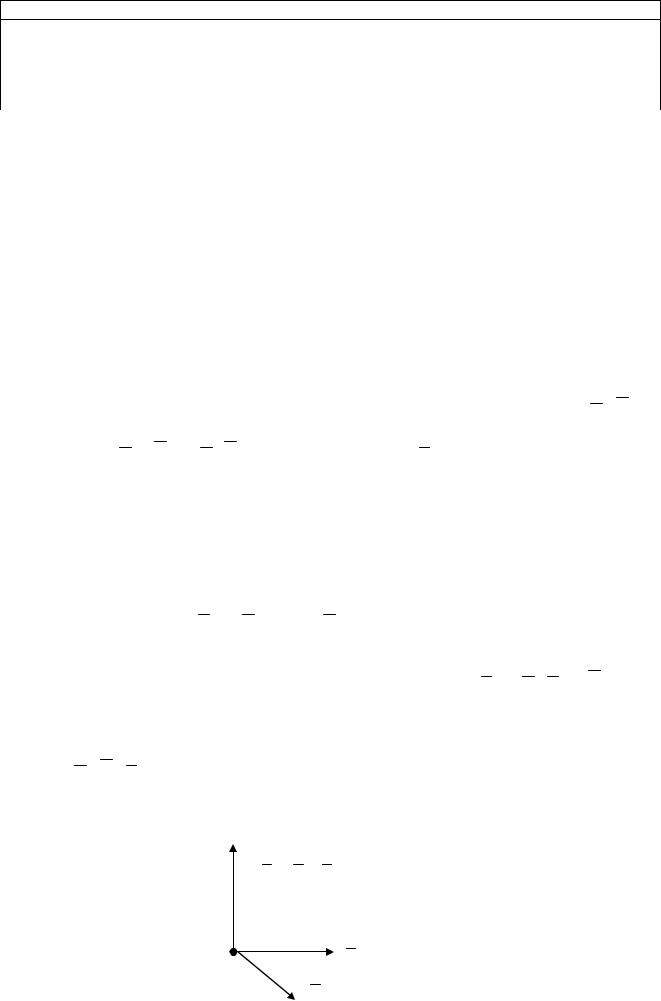
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 48 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Лекция 6 |
|
|
|
|
Векторное произведение векторов, смешанное |
произведение |
|||
векторов, |
основные |
свойства. |
Условия |
ортогональности, |
коллинеарности, компланарности векторов.
Цель: Изучить векторное и смешанное произведение векторов, их свойства, методы вычисления, условия ортогональности, компланарности и коллинеарности векторов.
Определение. Векторным произведением двух векторов a, b ,
обозначают |
a |
b [ |
a |
,b] называется вектор |
c |
удовлетворяющий трем |
||||||||||||||||||||
условиям: |
|
|||||||||||||||||||||||||
1) Модуль вектора равен площади параллелограмма, построенного на |
||||||||||||||||||||||||||
этих векторах |
|
|||||||||||||||||||||||||
|
|
|
|
c |
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
sin |
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
b |
|
|
b |
(6.1) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Вектор ортогонален перемножаемым векторам: c a, c b т.е.
ортогонален плоскости построенного на этих векторах параллелограмма
3) a, b, c составляют правую тройку векторов (рис.6.1).
c a b
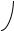 b
b
a

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 49 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Рис. 6.1
Свойства векторного произведения
1) |
a |
b b |
a |
(антикоммутативность) |
|
|||||||||||||||||||||||
|
|
Свойство следует из перемены ориентации векторов; |
|
|||||||||||||||||||||||||
2) |
|
|
|
|
|
Скалярный |
множитель |
можно вынести |
за скобку |
|||||||||||||||||||
( |
a |
) |
|
|
|
( |
a |
|
|
); |
|
|
|
|
|
|
|
|
|
|
||||||||
b |
b |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
( |
a |
|
|
) |
c |
|
a |
|
c |
|
|
|
c |
|
|
||||||||||||
3) |
b |
b |
(дистрибутивность); |
|
||||||||||||||||||||||||
|
|
4) Векторный квадрат равен нуль-вектору: |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a |
0 |
(6.2) |
|||
Свойство непосредственно вытекает из определения векторного произведения
Теорема. Чтобы векторы a и b были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулю.
a |
b 0 |
a |
|| b |
(6.3) |
|
|
||
Доказательство. Докажем, что если векторы коллинеарны, то их |
||||||||
|
|
a |
и |
|
|
|||
векторное произведение равно нулю. Действительно, |
т.к. векторы |
b |
||||||
коллинеарны, значит, угол между ними составляет |
0 либо 180 . Тогда |
|||||||

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 50 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
sin 0, т.е. длина вектора, полученного в результате перемножения
коллинеарных векторов, равна нулю, это возможно только у нулевого вектора.
Докажем теперь, что если векторное произведение равно нулю, то векторы коллинеарны. Пусть оба вектора a и b ненулевые (в противном случае доказательство тривиально), тогда a 0 и b 0, поэтому
a b 0 только в том случае, если sin 0, т.е. векторы a, b должны быть коллинеарны.
Теорема. В ортонормированном базисе декартовой прямоугольной системы координат i, j, k компоненты векторного произведения могут
быть вычислены по формуле:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
j |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
b |
|
|
|
1 |
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.4) |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
a |
1 |
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
3 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
i |
|
j |
k |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
где |
|
, |
b |
i |
j |
k |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Доказательство. Поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k k 0 |
и |
|||||||||||||||||||||||||||||||||||||||||||||
i |
i |
|
j j |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
i |
j k , |
|
|
j i k , |
|
|
|
j k i , |
|
k j i , |
k i j, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i k j
тогда a b ( 1i 2 j 3k) ( 1i 2 j 3k)
