Конспект лекций по алгебре

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

( )a a a (дистрибутивность).

3.Умножение векторов на число дистрибутивно относительно сложения векторов (a b) a b

4.1 a a.

Применяя линейные операции над векторами мы можем составлять суммы векторов умноженных на некоторые вещественные числа.

комбинацией векторов a1, a2, , ak.

С помощью введенных выше линейных операций мы можем преобразовать выражения, составленные из линейных комбинаций:

раскрывать скобки, приводить подобные члены, переносить некоторые слагаемые в другую часть равенства с противоположным знаком.

Свойства линейной комбинации

1.Если a1, a2, , ak– параллельны, то каждая их линейная комбинация параллельна им.

2.Если a1, a2, , ak – компланарны, то каждая их линейная комбинация компланарна с ними.

только при условии, что 1 2 ... k 0, тогда линейная комбинация

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

1a1 2a2 ... kak 0 – нетривиальная линейная комбинация, то

говорят, что a1, a2,...ak - линейно зависимы. В противном случае, т.е. если

1a1 2a2 ... kak 0 – тривиальная линейная комбинация, то

a1, a2,...ak – линейно независимы.

Теорема. Векторы a1,a2,...ak линейно зависимы тогда и только тогда,

1a1 2a2 ... k ak 0.

a1 является линейной комбинацией остальных.

Достаточность. Докажем, что если один из векторов a1, a2,...ak

является линейной комбинацией остальных, то векторы линейно зависимы.

Пусть a1 2a2 3a3 ... kak – линейная комбинация остальных

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

векторов, тогда a1, a2,...ak – линейно зависимы, поскольку

a1 2a2 ... kak 0 при том, что 1 1 0.

Теорема.

1.Если хотя бы один из векторов a1, a2,...ak , является нулевым, то эти векторы линейно зависимы.

2.Любые два коллинеарных вектора линейно зависимы, и наоборот, два линейно зависимых вектора коллинеарные.

3.Каждые три компланарных вектора линейно зависимы, и наоборот,

три линейно зависимых вектора компланарны.

4. Каждые четыре вектора линейно зависимы.

Доказательство. (Приведем доказательство 1–го и 2–го утверждений теоремы, остальные доказываются аналогично).

1.Поскольку среди векторов есть нулевой, значит, в их линейной комбинации перед нулевым вектором может стоять любой ненулевой элемент, а перед остальными векторами будут стоять нулевые элементы, это

иозначает линейную зависимость векторов.

2.Докажем, что если два вектора a,b коллинеарны, то они линейно

зависимы. Если хотя бы один из векторов a,b нулевой, то они линейно зависимы в силу предыдущего утверждения теоремы.

Если оба вектора ненулевые, то из свойства коллинеарности векторов a,b следует, что существует действительное число такое, что

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

или ( 1)a b 0, поскольку и 1 отличны от нуля a и b линейно зависимы.

Докажем теперь, что два линейно зависимых вектора - a и b

коллинеарны. Поскольку a и b линейно зависимы, следовательно, по

произведения вектора на число, это и означает коллинеарность векторов a и

b.

Базис.

Определение. Базисом на прямой называется любой ненулевой вектор

лежащий на этой прямой или коллинеарный с ней.

Определение. Базисом на плоскости называются два неколлинеарных вектора лежащих на этой плоскости или параллельных ей, взятые в

пространства можно представить как линейную комбинацию этих векторов,

т.е. a 1e1 2e2 3e3. Числа 1, 2, 3 называются

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

1.Каждый вектор, параллельный какой-либо прямой, может быть разложен по базису на этой прямой.

2.Каждый вектор, параллельный какой-либо плоскости, может быть разложен по базису на этой плоскости.

3.Каждый вектор может быть разложен по базису в пространстве.

4.Компоненты вектора в каждом случае определяются однозначно.

Доказательство.

1. Поскольку вектор, параллельный прямой, и вектор, лежащий на прямой, ненулевые, существует число α такое, что a e,положим, что

a

. e

параллелепипеда, построенного на векторах 1e1, 2e2, 3e3.

4.Доказательство единственности разложения вектора по

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Определение. Аффинные координаты в пространстве определяются

заданием базиса и некоторой точкой O, называемой началом

координат. Аффинными координатами точки М называются координаты вектора OM (относительно базиса a,b, c).

Определение. В случае декартовой прямоугольной системы координат

Т.е. векторы i, j, k являются ортонормированным базисом декартовой

системы координат. Базисные векторы имеют координаты i (1,0,0),

j (0,1,0), k (0,0,1).

Тогда каждый вектор a может, и притом единственным образом, быть разложен по декартовому прямоугольному базису i, j, k , т.е. существует

такая тройка чисел x, y, z, что справедливо равенство a xi yj zk ,

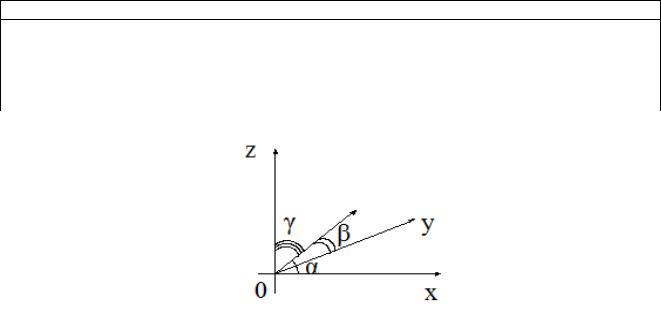
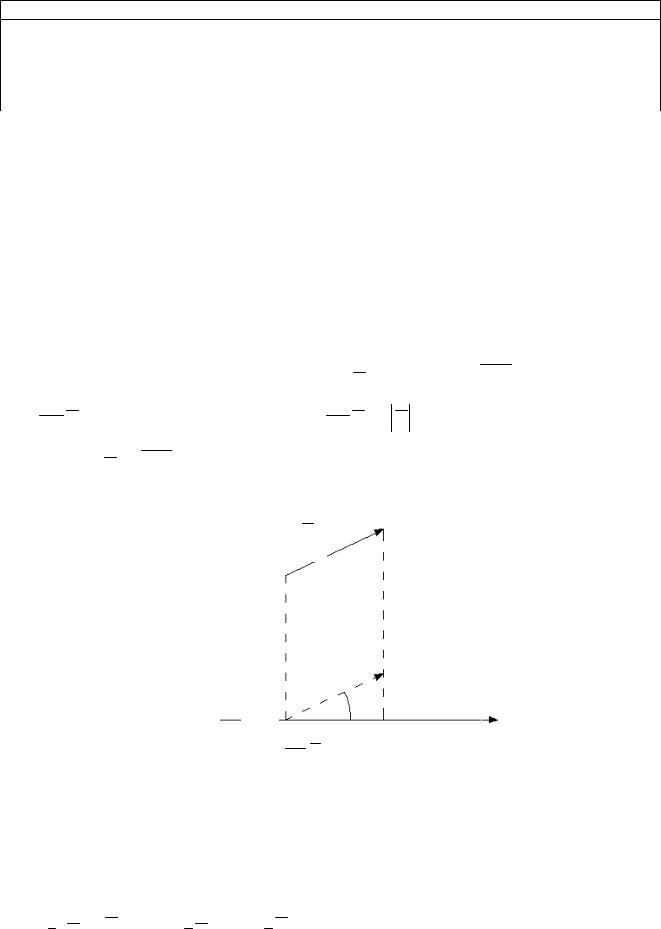
z a cos где , , – углы между вектором a и осями Ox,Oy, Oz

соответственно (рис. 4.5), а косинусы называются направляющими косинусами вектора.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Рис. 4.5

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Лекция 5

Проекция вектора и ее свойства. Деление отрезка в заданном отношении. Скалярное произведение векторов

Цель: Изучить понятие проекции и ее свойства, методику деления отрезка в данном отношении, скалярное произведение векторов, его свойства, физическое приложение.

Определение. Проекцией вектора a на вектор OB, обозначается

прOBа называется число, равное прOBа a cos где – угол между

векторами a и OB (рис.5.1).

a

прOBa

Рис. 5.1.

Свойства проекции

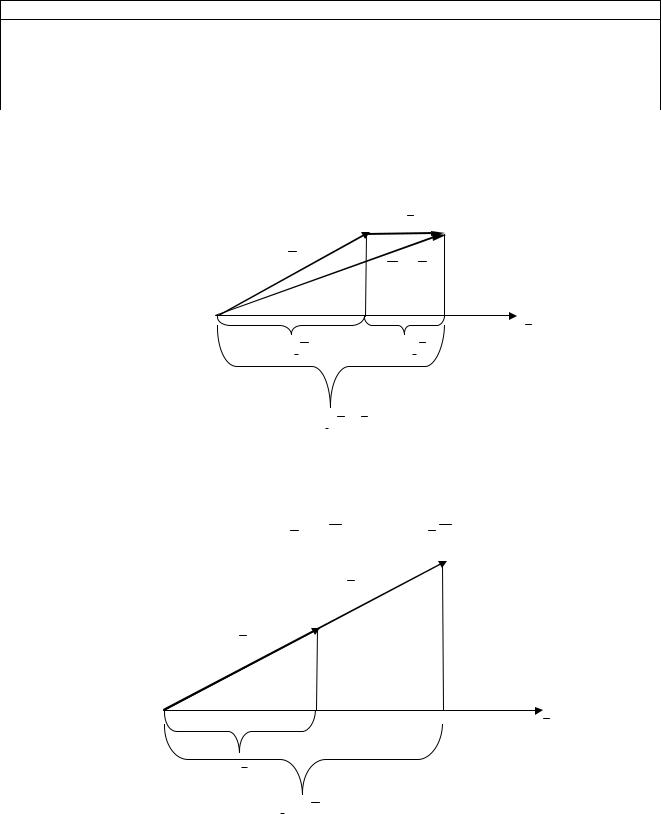
1)Проекция суммы векторов равна сумме проекций составляющих

пр c(а b) пр cа пр cb (рис. 5.2).