
Конспект лекций по алгебре
.pdf
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 21 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
w 3 |
|
1(cos |
0 2 |
|
isin |
0 2 |
) |
3 |
|
1 |
i; |
||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
3 |
|
3 |
|
|
|
2 |
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
0 4 |
|
0 4 |
|
|
|
|
|
|
1 |
i. |
||||||||
w 3 |
|
1(cos |
isin |
) |
|
|
3 |
||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
k |
|
3 |
|
3 |
|
|
|
2 |
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
Полученные значения являются вершинами правильного треугольника
вписанного в окружность радиуса 3
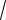 1.
1.
|
Пример. |
Корни |
|
n-ой |
степени |
из |
единицы |
|||||
wk |
n |
|
cos |
2k |
isin |
2k |
,k 0,1,2...,n 1 есть |
вершины |
правильного |
|||
1 |
||||||||||||
n |
|
|||||||||||
|
|
|
|
|
|
n |
|
|
|
|||
n-угольника, вписанного в единичный круг.
Определение. Многочленом одной переменной называется функция
f (z) anzn an 1zn 1 ... a1z a0, где a0,...an - действительные или комплексные коэффициенты, а n - целое неотрицательное число. Если an 0, n называют степенью многочлена и обозначают n deg f (z), а an- старшим коэффициентом. Многочлен f (z) называется нулевым, если все его коэффициенты равны нулю. Коэффициент a0 при z в нулевой степени называют постоянным или свободным членом.
Многочлены степени 1,2,3 называются соответственно линейными,
квадратичными (или квадратными), кубичными и т.д. В дальнейшем рассматриваются только действительные коэффициенты an.
Определение. |
Корнем многочлена |
f (z) anzn ... a1z a0 |
называется такое c |
, при котором f (c) 0. |
|

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 22 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Основная теорема алгебры. Всякий многочлен положительной степени имеет, по крайней мере, один корень действительный или
комплексный.
Деление многочленов. Из курса элементарной алгебры известен метод деления уголком для целых чисел, аналогичный алгоритм имеет место и для многочленов.
Пусть даны два многочлена: f (z) apz p ap 1z p 1 ... a0 и
g(z) b zq ... b , |
где |
a |
p |
,b 0, |
p q |
и, |
тогда |
||
q |
0 |
|
|
|
q |
|
|
|
|
многочлену f (z) |
сопоставляется |
одна |
|
и |
только одна пара |
многочленов |
|||
h(z), r(z), |
для |
которых |
|
f (z) h(z)g(z) r(z), |
|||||
degr(z) degg(z), |
h(z) называют |
частным |
деления, |
а |
r(z) - |
||||
остатком. |
|
|
|
|
|
|
|
|
|
Если r(z) 0, тогда говорят, что |
f (z) делится на g(z). |
|
|||||||
Если многочлены имеют действительные коэффициенты, то h(z) и r(z) также имеют действительные коэффициенты.
Пример. Проверить, делится ли многочлен z3 6z2 12z 8 на
z 2.
Решение. Разделим многочлены столбиком, т.е.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 23 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
|
|
|
|
_ |
z3 6z2 12z 8 |
|
|
z 2 |
|
|
|
|
|
|||||
|
|
|
|
z3 2z2 |
|
|
|
z2 4z 4 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
4z2 12z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4z2 8z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4z 8 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4z 8 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0: |
|
|
|
|
|
|
|
|
|
|
|
Итак, |
многочлен z3 6z2 12z 8 делится на |
z 2 и может быть |
||||||||||||||||
представлен в виде z3 6z2 |
12z 8 (z 2)(z2 |
4z 4). |
|
|||||||||||||||
Теорема |
Безу. |
Число |
z c |
является |
корнем |
многочлена |
||||||||||||
f (z) a |
n |
zn |
a |
n 1 |
zn 1 ... a z a |
0 |
тогда |
и |
только |
тогда, |
когда |
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
f (z) делится на линейный многочлен ( z c). |
|
|
|
|
|
|
|
|||||||||||
Доказательство. |
В результате деления |
f (z) |
на |
( z c) |
имеем |
|||||||||||||
f (z) (z c)h(z) r(z). |
Степень |
r(z) 1, |
значит |
r(z) const |
||||||||||||||
тогда подставим c в f (z), |
получим r f (c), следовательно |
f (c) 0 и |
||||||||||||||||
f (z) (z c)q(z). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Теорема. |
При делении |
f (z) на (z a), остаток r(z) f (a), т.е. |
||||||||||||||||
f (z) (z a)h(z) f (a).

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
|
Лист |
|
номер: |
находится на кафедре |
|
стр. 24 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
|
анализа |
|
|
Пример. Проверить, делится ли многочлен 7z4 12z2 |
10z 8 на |
|||
z 2. |
|
|
|
|
Решение. Разделим многочлены столбиком, т.е.
7z4 12z2 10z 8 |
|
z 2 |
_ |
|
|
|
7z3 14z2 40z 70 |
|
7z4 14z3 |
|
14z3 12z2
_
14z3 28z2
40z2 10z
_
40z2 80z
70z 8
_
70z 140
148;
степень остатка меньше степени делителя, останавливаем деление.
Итак, многочлен 7z4 12z2 10z 8 |
не делится на z 2 и может |
||
быть представлен в виде (z 2)(7z3 14z2 |
40z 70) 148. |
||
Проверить, правильно ли выполнено деление можно, используя |
|||
предыдущую |
теорему, |
согласно которой |
f (2) 148, действительно, |
f (2) 7 24 |
12 22 |
10 2 8 112 48 20 8 148, значит |
|
деление выполнено правильно.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 25 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Определение. |
Число c называется k– кратным корнем многочлена |
||||||||||
f (z), если |
f (z) |
делится |
|
на (z c)k, |
но не делится на (z c)k 1. |
||||||
Корень кратности 1 называют простым корнем. |
|
|
|
||||||||
Теорема. |
Если |
c1,...,cr - корни многочлена |
f (z)степени |
n – |
|||||||
кратности |
k1,...,kr |
соответственно |
и |
k1 k2 |
... kr n, |
тогда |
|||||
f (z) (z c )k1 |
...(z c |
r |
)kr h(z), |
где |
h(z) |
– |
многочлен степени |
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
((n (k1 |
kr )) такой, что h(ci) 0,i 1,...,r. |
|
|||||||||
Доказательство данной теоремы следует из теоремы Безу.
Правило определения кратности корня
Пусть c– корень кратности k многочлена |
f (z) степени n, тогда |
|
|||||
f (z) (z c)k h(z), |
f (c) 0, где h(c) 0`и degh(z) n k` |
||||||
|
k 1 |
|
|
|
k |
|
где |
f (z) k(z c) |
|
h(z) h (z)(z c) |
|
, f (c) 0, |
|||
degh1(z) n k 1, продолжая вычислять производные на k– ом шаге получим,
f (k)(z) k!h(z) h~1 |
(z)(z c) h~ |
(z)(z c)k |
, |
т.к. |
|
k |
|
|
|
h(c) 0, следовательно, |
f (k)(c) 0, тогда можно |
предложить |
||
следующее правило для вычисления кратности корня многочлена.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 26 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Для того чтобы определить кратность корня c |
многочлена f (z), |
вычисляем значения производных f (z) в точке |
c и как только |
f (k)(c) 0, тогда k - кратность корня. |
|

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 27 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Лекция 4
Векторная алгебра. Понятие вектора, координаты, модуль вектора.
Линейные операции над векторами. Базис
Цель: Изучить понятие вектора, равенства векторов, как определяются координаты вектора его модуль, линейные операции над векторами и их свойства, понятие базиса.
Определение. Направленный отрезок (упорядочивающий пару точек)
будем называть вектором и обозначать a, AB, где точку A называют
началом вектора, а B– его концом (рис.4.1).
Необходимо знать, что в печатных изданиях часто векторные величины и векторы обозначают жирным шрифтом, без стрелки
Вектор, у которого начало и конец совпадают, будем называть нулевым
вектором
В
a
А
Рис. 4.1
Расстояние между началом и концом вектора называется его длиной,
модулем или абсолютной величиной вектора и обозначают a , AB .
Векторы называются коллинеарными, если существует прямая, которой эти векторы параллельны, пишут a ||b . Коллинеарные векторы могут быть

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 28 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
сонаправленными (направлены в одну сторону), и противоположно направленными. Обозначается соответственно a b, a b.
Векторы называются компланарными, если существует плоскость,
которой они параллельны.
Нулевой вектор считается коллинеарным любому вектору т.к. не имеет направления.
Свойство. Если вектор a коллинеарен ненулевому вектору b, то существует действительное число такое, что a b.
Определение. Два вектора a,b считаются равными, если выполнено три условия: 1) их модули равны, 2) они параллельны, 3) направлены в одну сторону.
О равенстве векторов стоит поговорить отдельно, т.к. оно существенно отличается от равенства чисел. Два равных числа могут рассматриваться как одно и тоже. С векторами все иначе.
Из курса физики известно, что сила может быть изображена вектором.
Но, силы изображаемые равными направленными отрезками производят,
вообще говоря различные действия. Так сила действующая на упругое тело изображается направленным отрезком, который не может быть никуда перенесен из данной точки. Т.е. он характеризуется направлением и точкой приложения и называется приложенным вектором.
Сила действуещая на абсолютно твердое тело, изображается скользящим вектором, который может быть перенесен не в любую точку пространства, а
лишь вдоль прямой на которой он лежит.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 29 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Все остальные равные вектора (множество направленных отрезков,
равных данному) называются свободными векторами, с которыми мы и будем работать.
Линейные операции над векторами
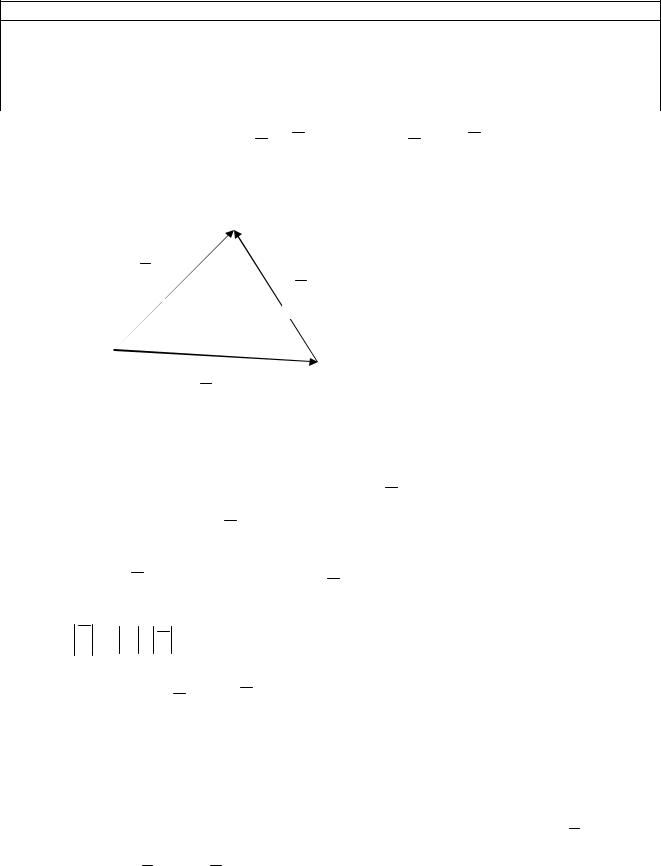
Определение. Суммой a b c называется вектор c , который может быть найден по следующим правилам (рис.4.2).
Свойства сложения векторов:
1)a b b a , (коммутативность);
2)a (b c) (a b) c, (ассоциативность);
3)прибавление нулевого вектора к любому другому не меняет последнего a 0 a;
4)вектор, противоположный вектору a, обозначается a. Их сумма дает нулевой вектор a ( a) 0.
a |
|
|
b |
|
|
|
|
|
|
|
b |
a |
|
|
|
|
|
|
|||
|
a |
b |
||||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
b |
|
|
||
Правило треугольника |
Правило параллелограмма |
Рис. 4.2
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 30 из 172 |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
|
|
|
анализа |
|
Определение. Разность a b есть сумма a ( b) (рис.4.3).
a  a b
a b
b
Рис.4.3
Определение. Произведением вектора a на вещественное число называется любой вектор b, удовлетворяющий следующим условиям:
а) вектор b коллинеарен вектору a;
б) b a ;
в) векторы a и b направлены одинаково если 0, и
противоположно направлены если 0,
Свойства умножения вектора на число
1.Для любых действительных чисел , и любого вектора a верно равенство ( )a ( a).(ассоциативность)
2.Умножение векторов на число дистрибутивно относительно сложения
чисел
