Файловый архив студентов. Файловый архив студентов.
1302 вуза, 5124 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Дальневосточный федеральный университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Конспект лекций по алгебре

.pdf
Скачиваний:
15
Добавлен:
01.05.2015
Размер:
1.08 Mб
Скачать
☆

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:

 

 

 

Идентификационный

 

Контрольный экземпляр

Лист

 

 

 

 

 

 

 

 

 

номер:

 

 

 

 

 

находится на кафедре

стр. 161 из

Дегтярева Н.Е.

 

 

 

 

 

 

 

 

 

 

 

Алгебры, геометрии и

172

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

анализа

 

 

 

x1 x2

x

 

 

 

 

 

 

 

 

 

 

 

 

x

oo

C

1 ;x

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1/

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

2

 

 

 

 

 

 

 

 

 

 

 

2

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x1

 

1 ( 1)

 

 

2 e1

 

 

 

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1/

2

 

 

 

б)x2, соответствующий. 1,

x2 ?

 

2

2

~ 2

2 rangA 1

 

 

2

 

2

 

 

 

2x1 2x2 0

x1 x2 x

 

 

 

 

1

 

1

 

 

 

xoo C ;x2

 

 

 

 

 

 

 

 

1

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

2

 

 

 

2 2

 

 

 

 

 

 

 

 

 

1/

 

 

x1

 

1 1

2 e2

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

1/

2

 

3) Составим матрицу перехода Q:

 

 

1/

2

1/

2

 

Q e1'

e2

'

 

 

 

 

.

2

1/

2

 

 

1/

 

Перепишем старые координаты через новые. X=QX’

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:

Идентификационный

 

 

 

 

Контрольный экземпляр

Лист

 

 

 

номер:

 

 

 

 

 

 

 

 

 

находится на кафедре

стр. 162 из

Дегтярева Н.Е.

 

 

 

 

 

 

 

 

 

 

 

Алгебры, геометрии и

172

 

 

 

 

 

 

 

 

 

 

 

 

 

 

анализа

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

x'

 

x

 

 

 

 

 

 

 

 

x'

 

 

 

 

 

 

 

y'

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1/ 2

 

 

 

 

 

 

 

2

2

 

1/ 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

,

 

 

 

 

 

 

1/2

1/ 2

y'

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

x'

 

 

 

 

 

 

 

y'

 

 

 

 

 

 

 

 

 

 

2

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Перепишем уравнение кривой второго порядка в новых координатах.

5x'2 y'2

 

 

 

1

 

 

 

1

 

 

 

 

 

1

 

 

1

 

 

 

 

6

 

 

 

x'

 

 

 

 

 

 

 

y'

4

 

 

 

 

x'

 

 

 

y'

7 0,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

2

 

 

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

2

 

1

2

 

 

 

 

 

 

 

 

 

 

 

5 x'

 

 

 

 

y'

 

 

 

 

 

 

10,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

x" x'

 

 

 

 

 

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

выполним

параллельный перенос и

получим

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y" y'

 

 

 

 

 

 

;

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

следующее уравнение

 

 

x"2 y"2

10,

 

 

5

 

 

 

x"2

 

 

y"2

 

1- уравнение гиперболы.

 

10

 

 

 

 

 

 

10

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:

Идентификационный

Контрольный экземпляр

Лист

 

номер:

находится на кафедре

стр. 163 из

Дегтярева Н.Е.

 

Алгебры, геометрии и

172

 

 

анализа

 

Поверхности второго порядка

Поверхности второго порядка определяются уравнением второй степени. Рассмотрим вращение линий второго порядка вокруг их осей симметрии.

. Поверхность S называется плоскостью вращения с осью d, если она составлена из окружностей, которые имеют центры на прямой d и лежат в плоскостях, перпендикулярных этой прямой.

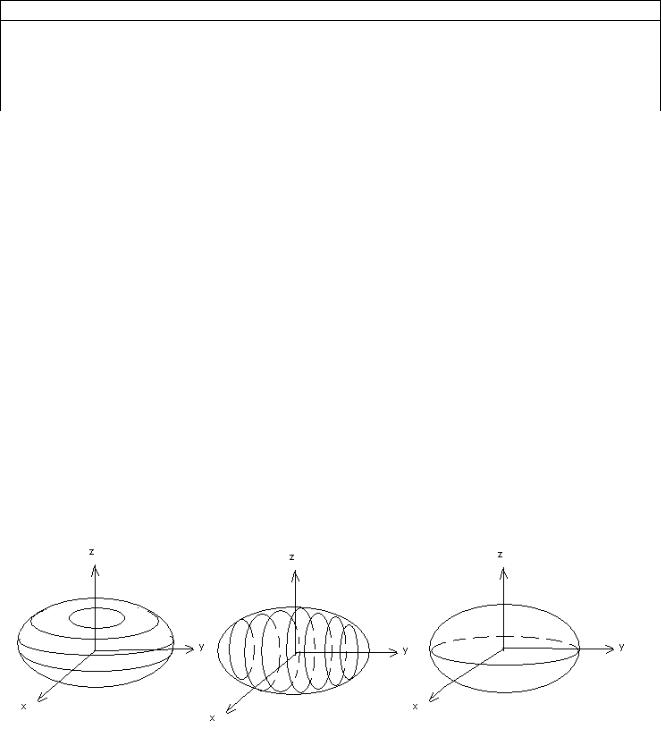
Эллипсоиды. Рассматриваем поверхности, которые получаются при вращении эллипса вокруг его осей симметрии.

Сжатый

вытянутый

эллипсоид

В первом и втором случае проекциями будут эллипсы и окружности, в

последнем – только эллипсы. Их каноническое уравнение записано в виде:

x

2

 

y

2

 

z

2

1

(18.1)

a2

b2

c2

 

 

 

 

Конусы. Рассмотрим на плоскости пару пересекающихся прямых.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:

Идентификационный

Контрольный экземпляр

Лист

 

номер:

находится на кафедре

стр. 164 из

Дегтярева Н.Е.

 

Алгебры, геометрии и

172

 

 

анализа

 

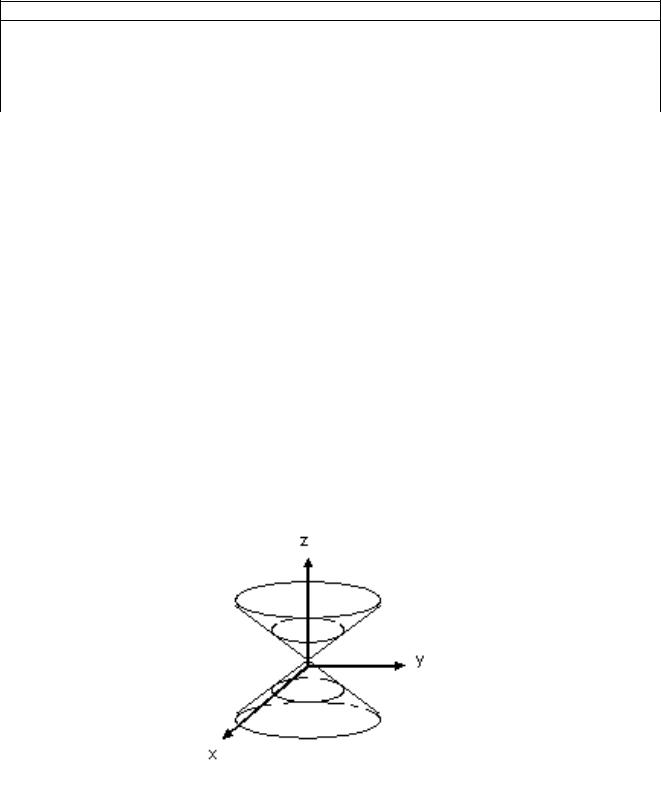
Поверхность получаемая вращением таких прямых, имеет уравнение:

a2(x2 y2) c2z2

0

(18.2)

Или a2(x2 y2) c2z2

и называется прямым круговым конусом. При сжатии его к оси Oy прямой конус переходит в конус второго порядка

a2x2 b2y2 c2z2

0

(18.3)

Сечение конуса второго порядка дает либо эллипсы либо окружности. Минус стоит перед той координатой, вокруг которой конус вращается.

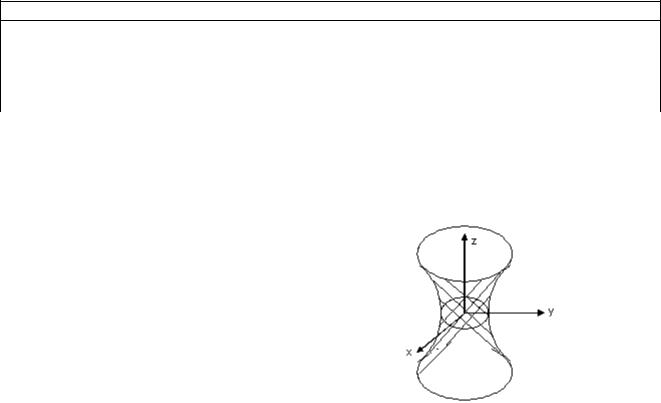
Гиперболоиды. Однополостные гиперболоиды получаются при вращении гиперболы вокруг той оси, которая ее не пересекает.

x

2

 

y

2

 

z

2

1

(18.4)

a2

b2

c2

 

 

 

 

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:

Идентификационный

Контрольный экземпляр

Лист

 

номер:

находится на кафедре

стр. 165 из

Дегтярева Н.Е.

 

Алгебры, геометрии и

172

 

 

анализа

 

Минус стоит перед координатой, вокруг которой вращается гипербола.

Интересным свойством однополостного гиперболоида является то, что его образующие прямолинейны.

Определение. Образующими называются прямые линии, всеми своими точками лежащие на поверхности.

Через каждую точку однополостного гиперболоида проходит две прямолинейные образующие. Их уравнения записываются в форме:

 

x

 

 

z

 

y

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

a

 

 

c

 

b

 

x

 

 

z

 

 

(18.5)

 

 

 

 

y

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

a

 

c

 

b

 

 

Если гиперболу вращать вместе с ее асимптотами, то асимптоты дадут нам конус вращения называемый асимптотическим конусом гиперболоида вращения.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:

Идентификационный

Контрольный экземпляр

Лист

 

номер:

находится на кафедре

стр. 166 из

Дегтярева Н.Е.

 

Алгебры, геометрии и

172

 

 

анализа

 

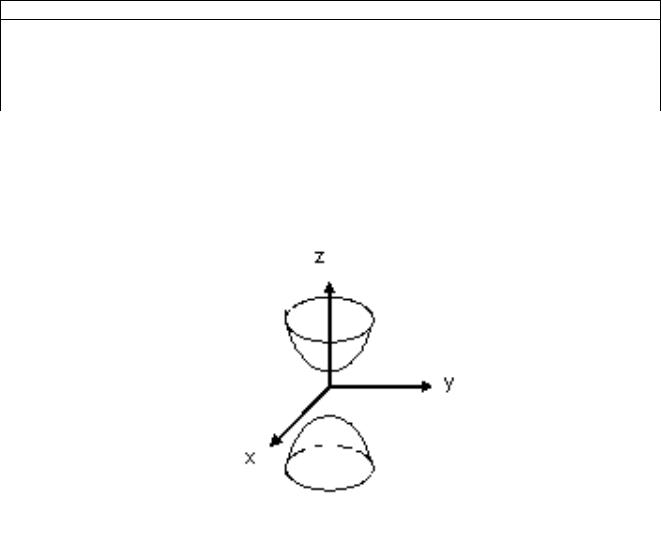
Двуполостный гиперболоид вращения – это поверхность вращения гиперболы вокруг той ее оси, которую она пересекает.

Его уравнение записывается в форме

 

z

2

 

 

 

x2

 

 

 

y

2

 

1

(18.6)

 

c2

 

a2

b2

 

 

 

 

 

 

 

 

или

x

2

 

 

 

y2

 

 

z

2

 

1

 

a

2

 

 

b2

 

c2

 

 

 

 

 

 

 

 

 

 

 

Также как и для однополостного асимптотический конус. Здесь двум ветвям гиперболы соответствуют две не связанные полости.

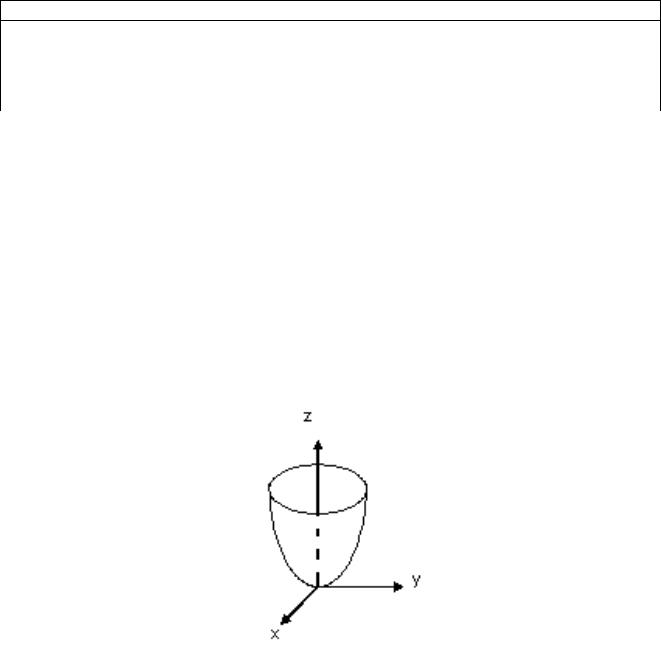
Элиптические параболоиды. При вращении параболы вокруг ее оси мы

получаем поверхность с уравнением:

x2 y2

2pz

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:

Идентификационный

Контрольный экземпляр

Лист

 

номер:

находится на кафедре

стр. 167 из

Дегтярева Н.Е.

 

Алгебры, геометрии и

172

 

 

анализа

 

называемую параболоидом вращения. В общем виде его уравнение записывается как

x

2

 

y

2

2z

(18.7)

a2

b2

 

 

 

Поверхность называется эллиптическим параболоидом. Его сечениями являются эллипсы и параболы.

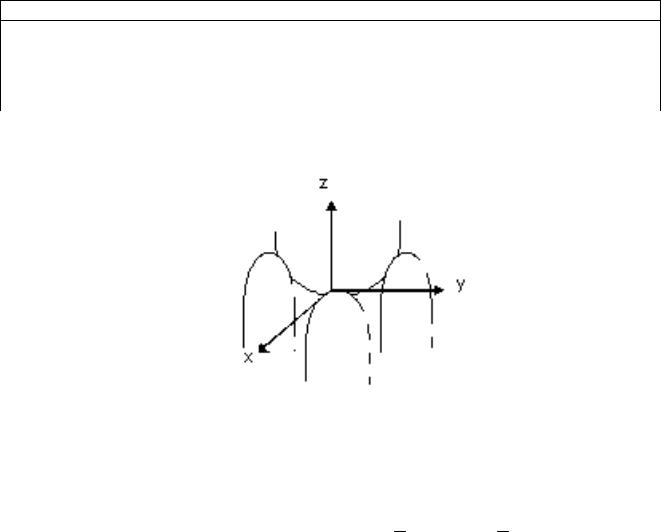
Гиперболический параболоид. Поверхность, которая имеет в некоторой

системе координат уравнение вида:

x

2

 

y

2

2z

(18.8)

a2

b2

 

 

 

Называется гиперболическим параболоидом. Т.е. на гиперболу надета парабола. Гиперболическим параболоид, как и однополостный гиперболоид имеет два семейства прямолинейных образующих. Его проекциями являются параболы и гиперболы.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:

Идентификационный

Контрольный экземпляр

Лист

 

номер:

находится на кафедре

стр. 168 из

Дегтярева Н.Е.

 

Алгебры, геометрии и

172

 

 

анализа

 

Приведение кривой 2-го порядка к каноническому виду.

Рассмотрим общее уравнение кривой 2-го порядка в евклидовом

пространстве, с ортонормированным базисом e1 (1;0), e2 (0;1):

a11x2 2a12xy a22 y2 2a13x 2a23y a33 0

1) Выделим квадратичную формулу a11x2 2a12xy a22 y2;

Приведем её к каноническому виду, для этого найдем собственные значения

A

a11

a12

,

 

A E

 

0 ,

2

- вещественные числа

 

 

 

a12

a22

 

 

 

 

1

 

 

 

 

 

 

 

 

 

a11x2 2a12xy a22 y2 1x 2 2 y 2.

2)Для того чтобы выразить x, y через x и y . Найдем координаты векторов нового базиса. За новый базис необходимо взять

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:

Идентификационный

Контрольный экземпляр

Лист

 

номер:

находится на кафедре

стр. 169 из

Дегтярева Н.Е.

 

Алгебры, геометрии и

172

 

 

анализа

 

ортонормированные собственные векторы квадратичной формы соответственно λ1 и λ2, для того чтобы их найти необходимо решить системы.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A E e 1 0

и A

2

E e 2 0

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e 1,e 2 ?

Матрица

 

перехода

от

старых

координат

к новым

координатам имеет вид:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

x

Q e 1

e 2

, т. е. x e 1

e 2

x ,

где

 

x

, x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Перейдя к новым координатам и выполнив все элементарные преобразования, получим канонический вид (параллельный перенос) кривой

2-го порядка в собственном базисе оператора квадратичной формы.

Пример. Привести кривую второго порядка к каноническому виду.

3x2 3y2 4xy 6x 4y 7 0

Решение.1) Найдем собственные числа

3

2

3

2

0

A

3

 

, (A E ) 0

2

 

2

 

 

3

 

2 6 5 0

1 5, 2 1, следовательно

3x2 4xy 3y2 5x'2 y'2

2)Найдем собственные векторы соответствующие собственным значениям и перейдем к новому ортонормированному базису:

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:

Идентификационный

Контрольный экземпляр

Лист

 

номер:

находится на кафедре

стр. 170 из

Дегтярева Н.Е.

 

Алгебры, геометрии и

172

 

 

анализа

 

а)x1, соответствующий. 5,

x1 ?

 

 

 

 

 

 

 

 

 

 

1

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

x'

 

 

 

 

 

 

 

y'

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1/ 5

2/

5 x'

5

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2/ 5

1/ 5

 

y'

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

x'

 

 

 

 

 

 

 

y'

 

 

 

 

 

 

 

 

 

5

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x1 x2

x

 

 

 

 

 

 

 

 

x

oo

C

1 ;x

1

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1/

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

2

 

 

 

 

 

 

 

2

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

x1

 

1 ( 1)

 

2 e1

 

 

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1/

2

 

б)x2, соответствующий. 1,

x2 ?

 

2

2

~ 2

2 rangA 1

 

 

2

 

2

 

 

 

2x1 2x2 0

x1 x2 x

1

1

xoo C ;x2

 

1

1

2

2

~ 2

2

 

 

2

2

 

 

rangA 1

2x1 2x2 0

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности