
Конспект лекций по алгебре
.pdf
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 151 из |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
172 |
|
|
анализа |
|
Получим каноническое уравнение эллипса x2b2 a2y2 a2b2 или
x2 |
|
y |
2 |
1 |
(17.6) |
|
a2 |
b2 |
|||||
|
|
|
||||
Где a - большая полуось эллипса, b - малая полуось эллипса
Из соотношения (17.5) получим формулу для фокального расстояния эллипса:
с |
a2 b2 |
(17.7) |
Если центр перенесен в точку с координатами (x0, y0), то каноническое уравнение эллипса имеет вид:
(x x )2 |
|
(y y ) |
2 |
|
|
0 |
|
0 |
|
1 |
(17.8) |
a2 |
b2 |
|
|||
|
|
|
|
Определение. Отношение расстояний между фокусами эллипса и длиной его большой оси. Называется эксцентриситетом и обозначается
|
2с |
|
|
|
(17.9) |
|
2а |
||||||
|
|
|||||
Т.к. для эллипса a c, то |
|
2с |
1 |
|
||
|
|
|||||
|
|
|
2а |
|
||
Сократим равенство (17.9) на 2 и возведя в квадрат выполним следующие преобразования:

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
|
|
|
Идентификационный |
|
|
Контрольный экземпляр |
Лист |
||||||||||||||||
|
|
|
|
|
|
|
номер: |
|
|
|
|
|
|
|
находится на кафедре |
стр. 152 из |
||||||||
Дегтярева Н.Е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Алгебры, геометрии и |
172 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
анализа |
|
|
|
|
||
|
2 |
|
с2 |
|
а2 b2 |
1 |
b |
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|||||||
|
а |
2 |
а2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
b |
2 |
|
|
|
|
|
|
b |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1,2 |
1 |
|
|
|
или |
|
|
|
|
|
|
|
1 |
|
. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
a |
|
|
|
|
||||
Из последних равенств видно, что эксцентриситет определяется отношением осей эллипса и наоборот, следовательно, чем больше эксцентриситет, тем более вытянута форма эллипса, при уменьшении эксцентриситета – эллипс стягивается в окружность.
Для |
произвольной |
точки |
|
эллипса |
M(x,y) |
||||
|
|
|
|
r |
|
a x. |
|||
r |
(x c)2 |
y2 |
a x, |
(x c)2 y2 |
|||||
1 |
|
|
|
|
2 |
|
|
|
|
|
r |
a x |
|
|
|
|
|
||
Система |
1 |
|
определяет параметрическое уравнение эллипса. |
||||||
|
r2 |
a x |
|
|
|
|
|
||
В полярной |
системе координат |
уравнение эллипса |
имеет вид |
||||||
x acos |
|
|
|
|
|
|
|
|
|
y bsin
Для эллипса вводят две прямые называемые директрисами, их
канонический вид: d |
x |
a |
, d |
2 |
x |
a |
. |
|
|
||||||
1 |
|
|
|
||||
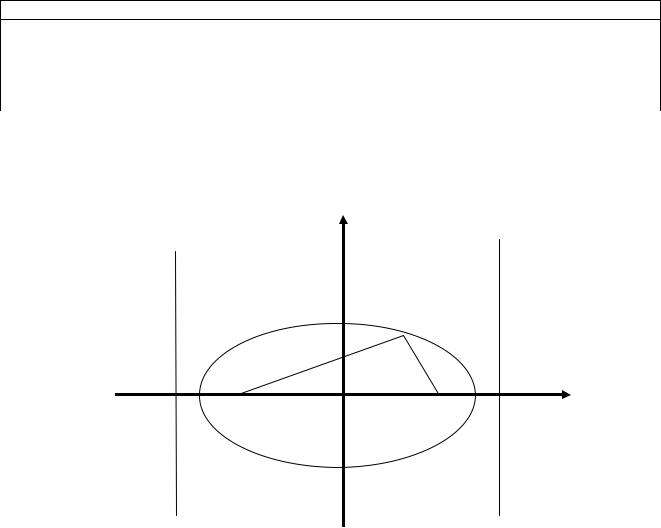
Определение. Эллипс - геометрическое место точек, для которых отношение фокального радиуса к расстоянию до соответствующей директрисы равно эксцентриситету эллипса (рис. 17.3):
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
|
|
Контрольный экземпляр |
Лист |
|
номер: |
|
|
находится на кафедре |
стр. 153 из |
Дегтярева Н.Е. |
|
|
|
Алгебры, геометрии и |
172 |
|
|
|
|
анализа |
|
|
|
r |
|
(17.10) |
|
|
|
|
|||
d
y
M
x
F1 F2
d1 d2
Рис.17.3
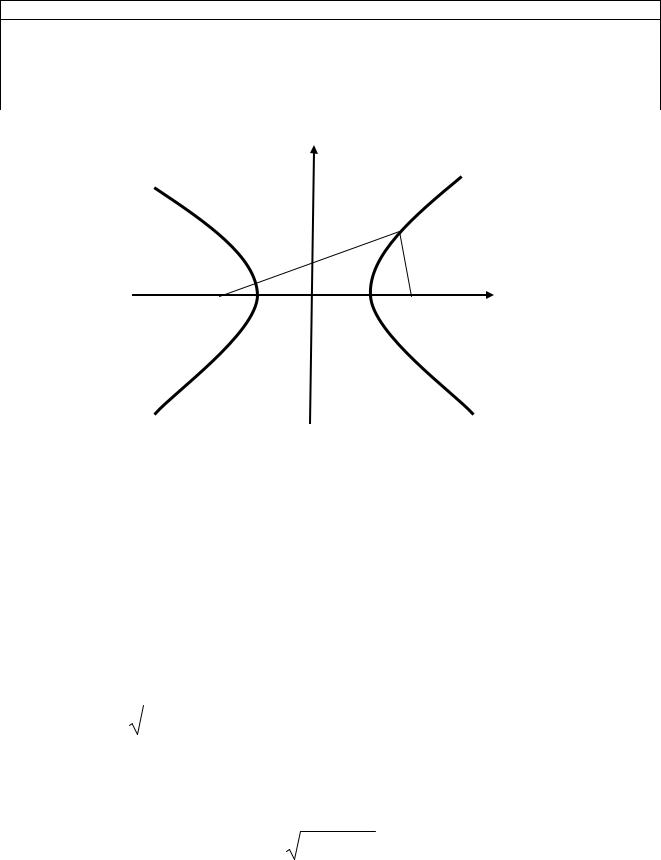
Определение. Гипербола – это геометрическое место точек, для каждой из которых разность расстояний от двух фиксированных точек плоскости
F1, F2, называемых фокусами, есть величина постоянная равная 2a.
Любая точка принадлежит гиперболе, если |
разность между ее |
фокальными радиусами равна2a(рис.17.3). |
|
r1 r2 2a |
(17.11) |
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 154 из |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
172 |
|
|
анализа |
|
y
M
r1
r2 x
F1 F2
Рис.17.4
поступая по аналогии с выводом уравнения эллипса, получим каноническое уравнение гиперболы
|
|
|
x2 |
|
y2 |
1 |
(17.12) |
|
|
|
a2 |
b2 |
|||
|
|
|
|
|
|
||
|
|
, 2a- действительная ось, 2b - мнимая ось, 2c- |
|||||
Где b |
c2 a2 |
||||||
фокальное расстояние.
Расстояние до фокуса гиперболы будет определятся равенством:
с |
b2 a2 |
|
|
(17.13) |
Прямые |
y |
b |
x |
(17.14) |
|
||||
|
1,2 |
a |
|
|
|
|
|
||
называются асимптотами гиперболы.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 155 из |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
172 |
|
|
анализа |
|
Если координаты центра смещены в точку (x0; y0), то каноническое
уравнение гиперболы имеет вид
(x x ) |
|
(y y ) |
2 |
|
|
0 |
|
0 |
|
1 |
(17.15) |
a2 |
b2 |
|
|||
|
|
|
|
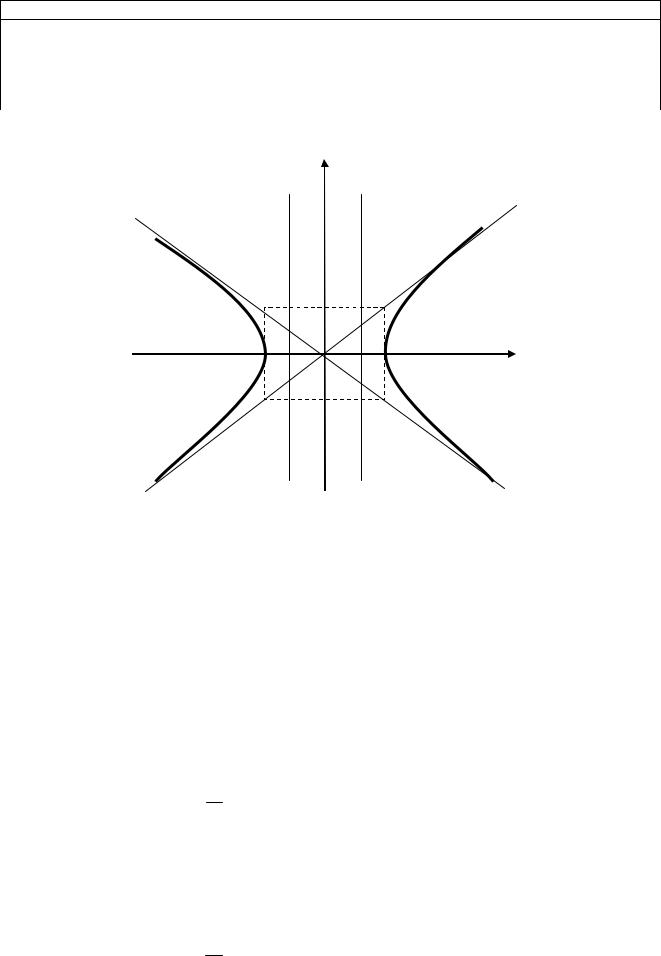
Прямоугольник, построенный на величинах a и b – называется основным прямоугольником гиперболы (рис. 17.5).
Эксцентриситет гиперболы определяется как отношение фокального
расстояния к действительной оси |
2с |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2а |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
b 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
c |
2 |
|
|
a2 b2 |
|
|
|
b 2 |
|
b |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
, 1 |
|
|
или |
|
|
|
|||||||
|
a |
2 |
|
|
a2 |
|
|
|
a |
|
||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
a |
|
|
|
|
|
|
|
||||||||
|
|
т.е. эксцентриситет гиперболы характеризует форму основного |
||||||||||||||||||||||||
прямоугольника, и следовательно форму гиперболы. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Определение. |
Две прямые, ортогональные той оси гиперболы, которая |
|||||||||||||||||||||||
ее |
пересекают и |
расположенные |
симметрично |
относительно |
центра на |
|||||||||||||||||||||
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
расстоянии |
|
|
от него называются директрисами гиперболы. Обозначаются |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
d2, d2 (рис.17.5).
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 156 из |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
172 |
|
|
анализа |
|
y
|
b |
|
F1 |
a F2 |
x |
d1 |
d2 |
y2 |
y1 |
|
Рис.17.5
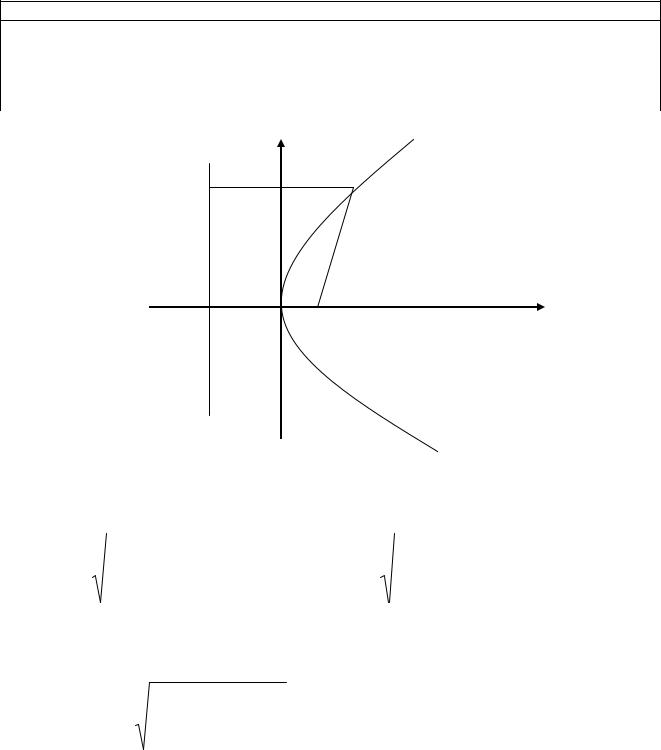
Определение. Парабола – это геометрическое место точек, для каждой из которых расстояние от некоторой фиксированной точки F, называемой фокусом равно расстоянию до некоторой фиксированной прямой d,
называемой директрисой (рис. 17.6):
r d |
(17.16) |
Расстояние OF p – называется фокальным расстоянием параболы, а
2
параметр p - параметром параболы. Т.к. для параболы c a, то 1.
Выведем уравнению параболы, используя формулу (17.16) и то
обстоятельство, что F(p; 0), M(x; y).
2
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 157 из |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
172 |
|
|
анализа |
|
|
y |
M |
|
|
d |
|
r
p x
F
|
|
|
|
Рис. 17.6 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
P |
2 |
|
|
|
P |
2 |
|
|||
d |
x |
|
|
(y y)2 , |
r |
x |
|
|
y2 . |
|||
2 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
Приравниваем d r и возводим в квадрат:
|
P |
|
|
P 2 |
y2 |
|
x |
|
|
x |
|
|
|
|
2 |
|||||
2 |
|
|
|
|
||
Избавляемся от корня повторным возведением в квадрат
|
2 |
|
p |
|
p2 |
|
2 |
|
p |
p2 |
|
2 |
|
x |
|
2 |
|
x |
|
x |
|
2 |
|
x |
|
y |
|
|
|
|
|
2 |
4 |
|
|||||||
|
|
2 |
4 |
|
|
|
|
|
|
||||
Приходим к каноническому уравнению параболы
y2 2px |
(17.17) |

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
||
|
номер: |
|
находится на кафедре |
стр. 158 из |
|
Дегтярева Н.Е. |
|
|
Алгебры, геометрии и |
172 |
|
|
|
|
анализа |
|
|
Если вершина параболы смещена в точку (x0, |
y0), то каноническое |
||||
уравнение имеет вид: |
(y y )2 |
2p(x x ) |
|
||
|
|
|
0 |
0 |
|

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 159 из |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
172 |
|
|
анализа |
|
Лекция 18
Приведение кривой 2-го порядка к каноническому виду.
Рассмотрим общее уравнение кривой 2-го порядка в евклидовом
пространстве, с ортонормированным базисом e1 1,0 ,e2 0,1 ,
a11x2 2a12xy a22 y2 2a13x 2a23y a33 0
1) Выделим квадратичную форму a11x2 2a12xy a22 y2;
Приведем её к каноническому виду, для этого найдем собственные значения
A |
a11 |
a12 |
, |
|
A E |
|
0 |
, |
2 |
- вещественные числа |
|
|
|
||||||||||
|
a12 |
a22 |
|
|
|
|
1 |
|
|
|
|
|
a11x2 2a12xy a22 y2 |
1x 2 2 y 2. |
|||||||||
следовательно |
|||||||||||
2) Для того чтобы выразить x, y через |
|
x и |
y , найдем координаты |
||||||||
векторов нового |
базиса. За новый |
|
базис |
необходимо взять |
|||||||
ортонормированные собственные векторы квадратичной формы соответственно λ1 и λ2, для того чтобы их найти необходимо решить системы.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A E e 1 0 |
и A |
2 |
E e 2 0 |
|
|
|
|
|||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e 1,e 2 ? |
Матрица |
|
перехода |
от |
старых |
координат |
к новым |
|||||||||||||||||||||||
координатам имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
Q e 1 |
e 2 |
, т. е. x e 1 |
e 2 |
x , |
где |
|
x |
, x |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра
Разработала: |
Идентификационный |
Контрольный экземпляр |
Лист |
|
номер: |
находится на кафедре |
стр. 160 из |
Дегтярева Н.Е. |
|
Алгебры, геометрии и |
172 |
|
|
анализа |
|
Перейдя к новым координатам и выполнив все элементарные преобразования, получим канонический вид (параллельный перенос) кривой
2-го порядка в собственном базисе оператора квадратичной формы.
Пример. Привести кривую второго порядка к каноническому виду.
3x2 3y2 4xy 6x 4y 7 0
Решение.1) Найдем собственные числа
3 |
2 |
3 |
2 |
0 |
||
A |
3 |
, |
(A E ) 0 |
2 |
|
|
2 |
|
|
3 |
|
||
2 6 5 0
1 5, 2 1, следовательно
3x2 4xy 3y2 5x'2 y'2
2) Найдем собственные векторы соответствующие собственным значениям и перейдем к новому ортонормированному базису:
а) x1, соответствующий. 5,
x1 ?
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
2 |
2 |
~ |
2 |
2 |
||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x' |
|
|
|
|
|
|
|
y' |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1/ 5 |
2/ |
|
5 x' |
||||||||||||||||||||||||||
|
5 |
5 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
rangA 1 |
|
|
||||||||||
|
1/ |
5 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2/ 5 |
|
y' |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
x' |
|
|
|
|
|
|
|
y' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
5 |
5 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2x1 2x2 0
