Конспект лекций по алгебре

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

где Xoo- общее решение соответствующей однородной системы, а Xчн-

частное решение неоднородной системы.

Для более простого нахождения частного решения, удобно взять свободные неизвестные равными нулю.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Лекция16.

Понятие линейного оператора. Основные свойства. Собственные числа и собственныевекторы.Квадратичныеформы.

Цель: Изучить понятия линейного оператора и его собственных чисел и собственныхвекторов,методыихнахождения.

Определение. Пусть V и W – линейные пространства размерности n и m соответственно, A – будем называть оператором, действующим из V и

W

A:V W

, y A x или y Ax, говорят что y – образ элемента x,

A: x y

а x – прообраз y.

Определение. Оператор A, действующий из V в W называется

линейным, если для x1,x2 V и C выполняются соотношения:

определяемый равенством A x Ax . 0x 0, где 0 нулевой оператор,

A 1 A, противоположный A оператор. Ix x - I –

тождественный или единичный оператор.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Фиксируем в линейном пространстве V базис e1,e2,...,en пусть x –

n

произвольный элемент V и x xk ek (разложение x по базису ek ). k 1

Рассмотрим akj матрицу линейного оператора в заданном базисе

e1,e2,...,en, это матрица столбцами которой являются координаты базисных векторов e1,e2,...,en. Причем единственный линейный оператор

A, матрицей которого в заданном базисе e1,e2,...,en будет матрица .

rang A rang , A - оператор.

A. При изменении базиса матрица линейного оператора A также изменится.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

новый базис, а U – матрица перехода от базиса e e , тогда матрица линейного оператора в двух базисах связаны следующим соотношением:

существует ненулевой вектор x такой, что Ax x, при этом x называется

Многочлен det A E называется характеристическим многочленом A.

Чтобы найти собственные числа нужно решить уравнение

A E 0.

Чтобы найти собственный вектор xi , соответствующий собственному

числу i необходимо решить систему A iE xi 0.

Свойства собственных значений и собственных чисел.

1.Каждый линейный оператор имеет собственное значение.

2.Собственные числа и векторы не всегда вещественные.

3.У симметричной матрицы собственные числа всегда вещественны.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

4.Собственные векторы соответствующие собственным значениям различные линейно независимы.

5.Если характеристический многочлен n-ой степени оператора A имеет

n – различных корней, то в некотором базисе матрица оператора A имеет диагональный вид.

6. Для того чтобы матрица A линейного оператора A в данном базисе

ek была диагональной, необходимо и достаточно, чтобы базисные векторы

ek были собственными векторами этого оператора.

Определение. Линейный оператор A называется самосопряженным,

если для любых x, y V выполняется равенство: Ax, y x, Ay .

Свойство самосопряженного линейного оператора

1.Собственные значения самосопряженного оператора вещественны.

2.Если A – самосопряженный оператор, то собственные векторы,

отвечающие различным собственным значениям этого оператора ортогональны.

Определение. Квадратичной формой называется однородный

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Если A – вещественная симметричная матрица, то форма называется

вещественной, A– самосопряженная.

В дальнейшем будем рассматривать вещественные квадратичные формы.

Теорема. Для каждой квадратичной формы существует базис, в котором она имеет канонический вид (т.е. представляет сумму квадратов) или такой вид в котором матрица квадратичной формы имеет диагональный вид.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Лекция 17

Кривые второго порядка

Цель: Изучить канонические уравнения линий второго порядка, их основные характеристики.

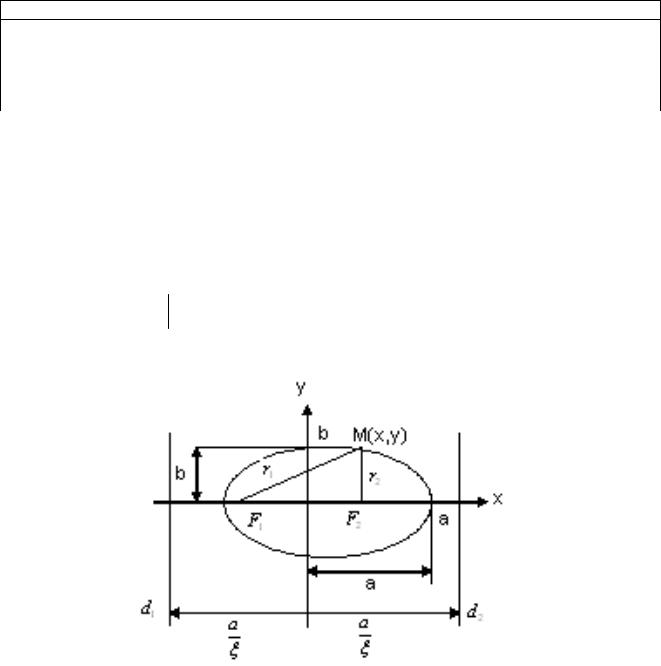
Определение. Окружность – это геометрическое место точек равноудаленных от некоторой фиксированной точки называемой центром окружности (рис.17.1).

если центр перенесен в точку с координатами (x0, y0), то

Рис. 17.1

Определение. Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости F1, F2,

называемых фокусами, есть величина постоянная равная 2a.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

точку M(x, y), принадлежащую эллипсу. Отрезки F1M , F2M

называются фокальными радиусами точки и обозначаются r1, r2 (Рис17.2).

Их постоянную сумму принято обозначать через 2a. Поэтому

Для вывода уравнения выразим фокальные радиусы через координаты

точек M, F1, F2:

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

(x c)2 y2 4a2 4a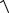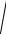(x c)2 y2 (x c)2 y2

Сокращаем на y2, раскрываем скобки

x2 2xc c2 4a2 4a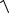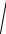(x c)2 y2 x2 2xc c2

сокращаем на 4, переносим корень влево

a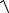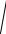(x c)2 y2 a2 xc

еще раз в квадрат: a2((x c)2 y2) a4 2a2xc x2c2

раскрываем и группируем

a2x2 2a2xc a2c2 a2y2 a4 2a2xc a2c2;

x2(a2 c2) a2y2 a2(a2 c2).

В полученном выражении введем обозначение