Конспект лекций по алгебре

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

базисным минором, если он отличен от нуля, а все миноры больших порядков, r 1,..., n равны нулю или их вообще нет, т.е rсовпадает с наименьшим из чисел m или n.

В матрице может быть несколько базисных миноров, но все они одного порядка.

Определение. Столбцы и строки стоящие на пересечении в базисном миноре называются базисными строками и базисными столбцами.

Определение. Рангом матрицы (обозначается Rg A rangA)

называется порядок базисного минора, или самый большой порядок для которого существует отличный от нуля минор.

Следствие. Квадратная матрица, определитель которой отличен от нуля имеет ранг равный ее размерности.

Вычисление ранга.

Метод окаймляющих миноров.

Суть метода заключается в последовательном вычислении миноров по возрастанию их порядка.

1 3 5 4

Пример: Вычислить ранг матрицы A 2 6 4 3

3 9 3 2

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Элементарными преобразованиями матрицу можно привести к виду,

когда ее строки будут содержать нули и не более одной единицы. Т.е. часть строк и столбцов представляют собой единичную матрицу (остальные содержат только нули). Тогда ранг матрицы равен количеству единиц.

В данных преобразованиях (2. и 3.) Ненулевые строки и столбцы есть базисные строки и столбцы. Минор построенный на данных строках и столбцах является базисным минором.

Свойства ранга матрицы.

1 Ранг произведения двух матриц не превосходит ранга сомножителей:

2 При умножении произвольной матрицы Aслева или справа на невырожденную матрицу её B ранг не изменяется. Другими словами, если det B 0, то

Теорема: (о базисном миноре) В произвольной матрице каждый столбец является линейной комбинацией базисных столбцов, а каждая стока – линейной комбинацией базисных строк.

Следствие: Если A квадратная матрица и det A 0 , то по крайней мере один из столбцов является линейной комбинацией остальных столбцов,

а так же одна из строк является линейной комбинацией остальных строк.

Теорема: (о ранге матрицы) Ранг матрицы Am n равен максимальному числу линейно независимых строк и столбцов в этой матрице.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Следствие: Максимальное число линейно независимых строк в матрице

равно максимальному числу линейно независимых столбцов в этой матрице.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Лекция 13

Линейные пространства.

Цель: ознакомится с понятие пространства, базиса, размерности,

преобразованием координат.

Определение. Множество L элементов x, y, z,.,.. любой природы называется линейным пространством, если выполнены следующие два правила: 1) существует правило, по которому любым x, y L, ставится в соответствие z x y, z L (сумма);

2) существует правило, по которому любому x L и для любого -

вещественного числа, ставится в соответствие u x, u L.

Указанные 2-е операции подчинены следующим аксиомам ( - любой):

1)x y y x, для x, y L;

2)x y z x y z , для x, y,z L;

3)Существует нулевой элемент 0, x 0 x, для x L;

принадлежащий L;

5)x x 0, где 0 L;

6)1 x x, для x L;

7)x x, для x L;

8)x x x, x L;

9)x y x y, x, y L.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Примеры конкретных линейных пространств.

1. An – n-мерное координатное пространство или совокупность строк содержащих n– вещественных чисел. Операция сложения и умножения на число определены следующим образом:

а) x1,x2,...,xn y1, y2,...,yn x1 y1,x2 y2,...,xn yn ;

б) x1,x2,...,xn x1, x2,..., xn .

Аксиомы 1-8 проверяются элементарно.

2. Множество x всех положительных вещественных чисел. Под суммой [x+y]=x*y (будем понимать произведение), а под умножением

[λ*x]=xλ, тогда нулевым элементом множества будет являться 1, а

противоположным x, 1, тогда аксиомы 1-8 легко проверяются.

x

3.Множество всех положительных вещественных чисел x , где сумма

иумножение на число определяются стандартным образом [x+y]=x+y, [λx]= λx не является линейным пространством.

4. Аналогично множество всех многочленов степени n не является линейным пространством, т. к. сумма может оказаться степени < n.

Определение. Линейной комбинацией элементов x, y,...,z пространства

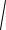2 ... 2 0, а x y ... z 0.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

x, y,...,z - неявляющиеся линейно зависимыми называют линейно

независимыми.

Определение. Совокупность линейно независимых элементов

e1,e2,...,en пространства L называется базисом этого пространства, если

умножении произвольного элемента на любые числа α все координаты этого элемента умножаются на α.

Тогда в силу аксиом 1-8 x y x1 y1 e1 ... xn yn en,

x x1 e1 ... xn en.

Определение. Линейное пространство L называется n-мерным, если в нем существует n-линейно независимых элементов, а любые (n 1)

элементы уже являются линейно зависимыми, n – называют размерностью

L и обозначают dimL n. Линейное пространство L называют

бесконечномерным, если в нем существует любое число линейно независимых элементов.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

элементов этого пространства образуют базис.

Если линейное пространство L имеет базис, состоящий из n элементов,

следовательно, dimL n.

Определение (понятие линейного подпространства). Подмножество

~

L L и удовлетворяющее условиям:

1.если x, y L, то x y L;

2.если x L, R x L;

называется линейным подпространством (или просто

подпространством) пространства R.

~

Определение. Линейной оболочкой L элементов x, y,...,z называется

совокупность всех линейных комбинаций этих элементов, т. е. множество

Определение (новое определение ранга матрицы). Ранг произвольной матрицы A равен максимальному числу линейно независимых строк (или столбцов) этой матрицы.

Преобразование координат при преобразовании базиса n-мерного

линейного пространства