Конспект лекций по алгебре

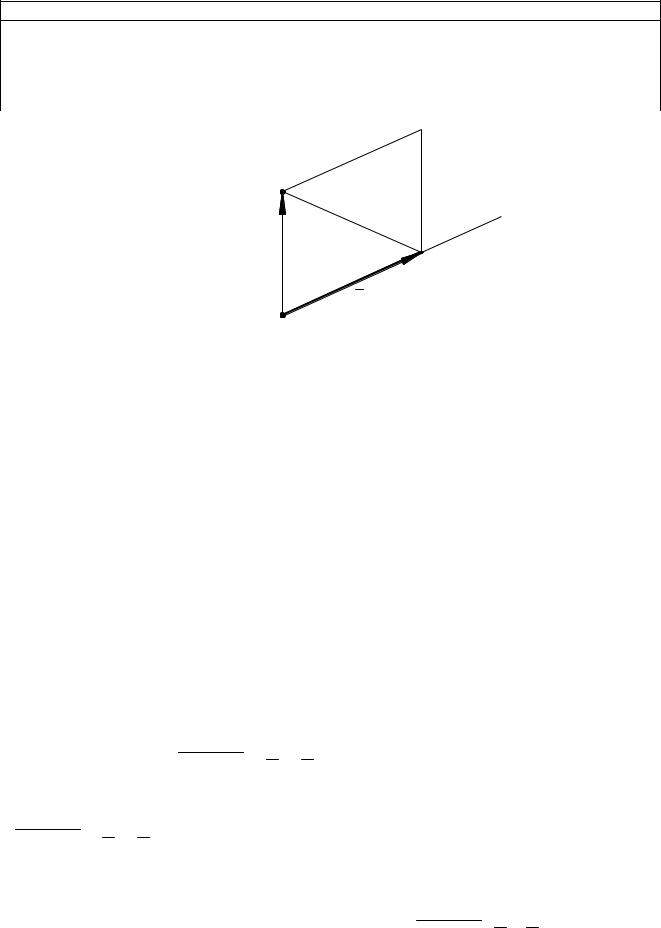
ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

M0

l

a

M1

Рис. 9.10

Задача 6. Найти расстояние между двумя скрещивающимися прямыми

(рис. 9.11).

Напомним, что две прямые называются скрещивающимися, если они не принадлежат одной плоскости.

Алгоритм действий при решении данной задачи может быть следующим:

1) проверяем, являются ли прямые скрещивающимися, для этого достаточно проверить будут ли направляющие векторы прямых и вектор,

соединяющий две произвольные точки, принадлежащие прямым,

компланарны, т.е. M1M0 a1 a2 0. Если смешанное произведение равно нулю, то прямые не являются скрещивающимися и наоборот, если

M1M0 a1 a2 0, тогда прямые скрещивающиеся;

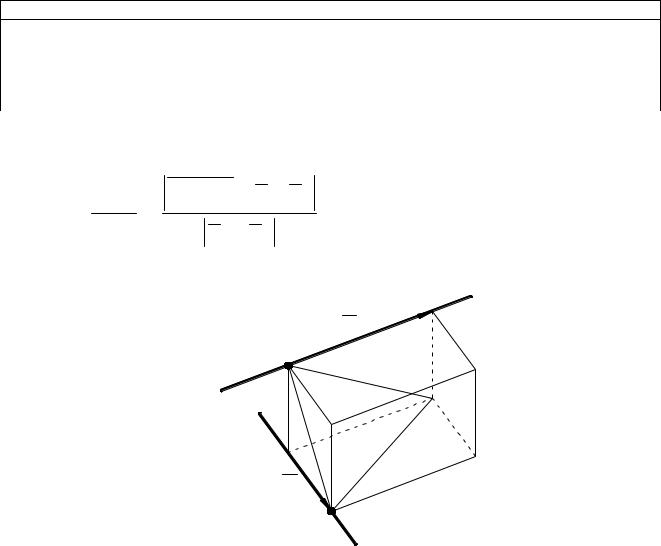
2) расстояние между скрещивающимися прямыми равно высоте параллелепипеда построенного на векторах M1M0, a1, a2, находим

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Лекция 10

Матрицы и действия над ними

Цель: Изучить понятие матрицы, виды матриц, основные понятия,

действия над матрицами и их свойства.

Определение: Система действительных или комплексных чисел (или функций) записанная в виде прямоугольной таблицы называется матрицей

содержащая некоторое количество m строк и n столбцов. Числа m и n

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

столбца. (i 1, m, j 1, n).

Для краткости матрицы иногда записывают в виде: A aij m n,

Определение: Матрица, у которой число строк равно числу столбцов называется квадратной. Для нее вводится понятие главной и побочной диагоналей. Главная диагональ идет из левого верхнего угла в правый нижний угол. Побочная – из верхнего правого угла в левый нижний.

Виды матриц:

1. Треугольные матрицы: все элементы лежащие выше или ниже главной (побочной) диагонали равны нулю.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

3.Симметричные матрицы: все ее элементы симметричны относительно главной диагонали.

4.Матрица, все элементы которой равны нулю называется

нуль-матрицей и обозначается O 0 m n

Матрица размерности m 1 называется матрицей столбцом, просто столбцом или вектор столбцом.

Матрица размерности n 1 называется матрицей строкой, просто строкой или вектор строкой.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Определение: матрицы называются равными, если они имеют одинаковые порядки и их соответствующие элементы равны: aij bij , для

любых i, j.

Из определения суммы матриц видим, что строки можно рассматривать как координаты векторов и соответственно производить операции над матрицами, как над векторами.

Свойства суммы матриц

1)A B B A (коммутативность);

2)(A B) C A (B C) (ассоциативность).

Определение. Произведением матрицы A aij m n на число , С

называется матрица D dij m n, элементы которой определяются по

формуле:

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Свойства умножения матрицы на число

1) A A A дистрибутивность относительно суммы числовых

множителей;

2) A B A B дистрибутивность относительно суммы матриц;

3) A A A ассоциативность относительно числового множителя;

4)1 А А;

5)0 А 0;

размерности (m p).

Из формулы Am n Bn p Сm p видно, что матрицы

перемножаются только в том случае, когда число столбцов первой матрицы,

совпадает с числом строк второй матрицы.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Формулу (10.3) можно рассматривать как совокупность скалярных произведений вектор-строк матрицы A на вектор-столбцы матрицы B.

Замечание. Каждый элемент матрицы С равен сумме произведений соответствующих элементов строки матрицы А, на столбец матрицы В.

Соответственно количество столбцов матрицы А должно совпадать с количеством строкматрицы В.

Свойства произведения матриц

1)A B B A (антикоммутативность);

2)A B C AC BC дистрибутивность относительно суммы матриц;

3)AB A B A B ;

Свойства нулевой и единичной матриц

1)АЕ ЕА для любой An n ;

2)АО ОА для любой An n;

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

AТ aji n m называется транспонированной по отношению к матрице A,

Если AT A, то A - симметрическая матрица.

Если AT A, то A - кососимметрическая матрица.

Свойства операции транспонирования матриц

1)AT T A;

2)A B T AT BT ;

3)AB T BT AT .

Определение. Действительная квадратная матрица Q,

удовлетворяющая условию Q 1 QT , называется ортогональной матрицей,

detQ 1.

Определение. Следом SpA – квадратной матрицы Ап п (аij )

n

называется сумма всех её диагональных элементов: SpA aii . i 1

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Лекция 11

Определители: вычисление и свойства

Цель: Изучить основные понятия темя, методы вычисления определителя, знать и уметь применять его свойства.

Всякую квадратную матрицу можно охарактеризовать числом, которое называется определитель или детерминант и может обозначаться одним из следующих символов: det A, , A, A, A

Прежде чем вычислять определитель введем в рассмотрение следующие определения.

строку и первый столбец. Все, что осталось от определителя есть искомый

5 6

минор: M11 .

8 9