вышмат

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

« НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙПОЛИТЕХНИЧЕСКИЙУНИВЕРСИТЕТ»

Л.И. Самочернова

ВЫСШАЯ МАТЕМАТИКА

Часть II

Рекомендовано в качестве учебного пособия Редакционно-издательским советом Томского политехнического университета

2-е издание, исправленное

Издательство Томского политехнического университета

2005

УДК 514.12 C17

Самочернова Л.И.

C17 Высшая математика. Часть II: учебное пособие / Л.И. Самочернова; Томский политехнический университет. – 2-е изд., испр. – Томск: Изд-во Томского политехнического университета, 2005. – 164 с.

Учебное пособие включает три раздела высшей математики: 1) введение в математический анализ (предел последовательности и функции, бесконечно малые и бесконечно большие величины, сравнение бесконечно малых, непрерывность функции, точки разрыва); 2) дифференциальное исчисление функции одной переменной (производная и дифференциал функции, применения дифференциального исчисления к исследованию функций); 3) интегральное исчисление (неопределенный интеграл, определенный интеграл, геометрические приложения определенного интеграла).

Пособие подготовлено на кафедре прикладной математики и предназначено для студентов ИДО, обучающихся по направлениям 080400 «Управление персоналом», 080200 «Менеджмент», 080100 «Экономика», 100700 «Торговое дело».

УДК 514.12

Рецензенты

Кандидат физико-математических наук, доцент кафедры алгебры ТГУ

С.Я. Гриншпон

Кандидат технических наук, доцент факультета систем управления ТУСУРа

А.И. Кочегуров

©Томский политехнический университет, 2005

©Самочернова Л.И., 2005

©Оформление. Издательство Томского политехнического университета, 2005

2

1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

1.1. Числовая последовательность и её предел

Определение 1. Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число xn , то гово-

рят, что задана числовая последовательность {xn}:

Другими словами, числовая последовательность – это функция натурального аргумента: xn = f(n).

Числа, составляющие последовательность, называются её членами, а xn – общим или n-м членом последовательности.

Пример числовой последовательности: 2, 4, 6, 8, ..., 2n, ...

Для этой последовательности x1 = 2, x2 = 4, x3 = 6,..., xn = 2n – общий член последовательности чётных чисел.

Пример 1. Зная общий член последовательности xn = n +n 2 , написать

её первые пять членов.

Решение. Давая n значения 1, 2, 3, 4, 5, получим x1 = 13; x2 = 24 ; x3 = 53 ; x4 = 64 ; x5 = 75 .

Вообщежепоследовательностьсобщимчленом xn = n +n 2 запишетсятак:

13 ,24 ,53 ,64 ,...,n +n 2 ,...

Отметим, что поскольку xn =f(n) есть функция, то есть, вообще говоря,

переменная величина, то для удобства будем в дальнейшем часто называть функцию xn переменной величиной, или просто переменной xn .

Ограниченные и неограниченные последовательности Определение 2. Последовательность {xn} называется ограниченной

сверху (снизу), если существует такое вещественное число М (число m), что каждый элемент xn последовательности {xn} удовлетворяет неравенству

xn ≤ M (xn ≥ m) .

При этом число М (число m) называется верхней гранью (нижней гранью) последовательности {xn}, а неравенство xn ≤ M (xn ≥ m) называется ус-

ловием ограниченности последовательности сверху (снизу).

3

Определение 3. Последовательность называется ограниченной с обеих сторон, или просто ограниченной, если она ограничена и сверху, и снизу, то есть, если существуют числа m и М такие, что любой элемент xn этой после-

довательности удовлетворяет неравенствам: m ≤ xn ≤ M .

Если последовательность {xn} ограничена и М и m – её верхняя и нижняя грани, то все элементы этой последовательности удовлетворяют неравенству

где А – максимальное из двух чисел |М| и |m|. Обратно, если все элементы последовательности {xn} удовлетворяют неравенству (1.2), то выполняются

также неравенства − A ≤ xn ≤ A и, следовательно, последовательность {xn}

ограничена. Таким образом, неравенство (1.2) представляет собой другую форму условия ограниченности последовательности. Уточним понятие неограниченной последовательности.

Последовательность {xn} называется неограниченной, если для любого положительного числа А найдется элемент xn этой последовательности, удовлетворяющий неравенству xn > A .

очевидно, неограниченная. В самом деле, каково бы ни было положительное число А, среди элементов этой последовательности найдутся элементы, превосходящие А.

Монотонные последовательности

Определение 4. Последовательность {xn} называется неубывающей

(невозрастающей), если каждый последующий член этой последовательности не меньше (не больше) предыдущего, то есть для всех номеров n справедливо неравенство xn ≤ xn+1 (xn ≥ xn+1) .

Неубывающие и невозрастающие последовательности объединяются общим наименованием монотонные последовательности. Если элементы монотонной последовательности {xn} для всех номеров n удовлетворяют не-

равенству xn < xn+1 (xn > xn+1) , то последовательность {xn} называется воз-

растающей (убывающей). Возрастающие и убывающие последовательности называются также строго монотонными.

Пример 2. Последовательность нечётных чисел 1, 3, 5, 7, ..., 2n–1, ..., где xn = 2n −1, – монотонно возрастающая.

4

Действительно, xn+1 − xn = [2(n +1) −1]−(2n −1) = 2 , так что xn+1 − xn > 0, т. е. xn+1 > xn при всех n.

Предел последовательности

Определим одно из важнейших понятий математического анализа – предел последовательности, или, что то же самое, предел переменной величины xn , пробегающей последовательность x1,x2 ,...,xn ,...

Определение 5. Постоянное число а называется пределом последовательности x1,x2 ,...,xn ,... или пределом переменной xn , если для любого

сколь угодно малого положительного числа ε можно указать такое натуральное число N, что для всех членов последовательности с номерами n>N выполняется неравенство

Тот факт, что последовательность (1.1) имеет своим пределом число а, обозначается так:

( lim есть сокращённое обозначение латинского слова limes, означающего «предел»).

Последовательность, имеющую пределом число а, иначе называют последовательностью, сходящейся к а. Последовательность, не имеющая предела, называется расходящейся.

Замечание. Величина N зависит от ε, которое мы выбираем произвольным образом (N=N(ε)). Чем меньше ε, тем N, вообще говоря, будет больше. Исключением является случай, когда последовательность состоит из одинаковых членов.

Решение. Выберем произвольно положительное число ε и покажем, что для него можно найти такое натуральное число N, что для всех номеров

После приведения к общему знаменателю в левой части неравенства (1.4) получим

5

Но если 1/(n +1) <ε, то и 1/(n +1) <ε. Из последнего неравенства следу-

ет, что n +1 >1/ε, n >1/ε–1. Следовательно, за N можно взять наибольшее целое число, содержащееся в (1/ε – 1), то есть Е(1/ε – 1). Тогда неравенство (1.4) будет выполняться при всех n >N. Если окажется, что Е(1/ε – 1) ≤0, то N можно взять равным 1. Поскольку ε брали произвольно, то этим и доказано, что 1 есть предел последовательности с общим членом xn = n /(n +1) . В част-

ности, если ε = 0,01, то N = Е(1/ 0,01 −1)=Е(100 – 1)=99; если ε=1/2, то

N=Е(1/ 0,5 −1)=1 и т. д. Выбранные таким образом N для различных значений ε будут наименьшими из возможных.

Геометрическая интерпретация предела числовой последовательности

Числовую последовательность (1.1) можно рассматривать как последовательность точек прямой. Точно так же и о пределе можно говорить как о точке на прямой. Так как неравенство xn − a < ε равносильно неравенству – ε < xn − a < ε,

которое, в свою очередь, равносильно такому a – ε < xn < a + ε, то определение

пределачисловойпоследовательностиможносформулироватьитак. Определение 6. Точка а называется пределом последовательности то-

чек (1.1), если, какую бы окрестность ( a – ε, a + ε) точки а мы ни задали, найдётся такое число N, что все точки последовательности (1.1) с номерами n > N попадут в заданную окрестность.

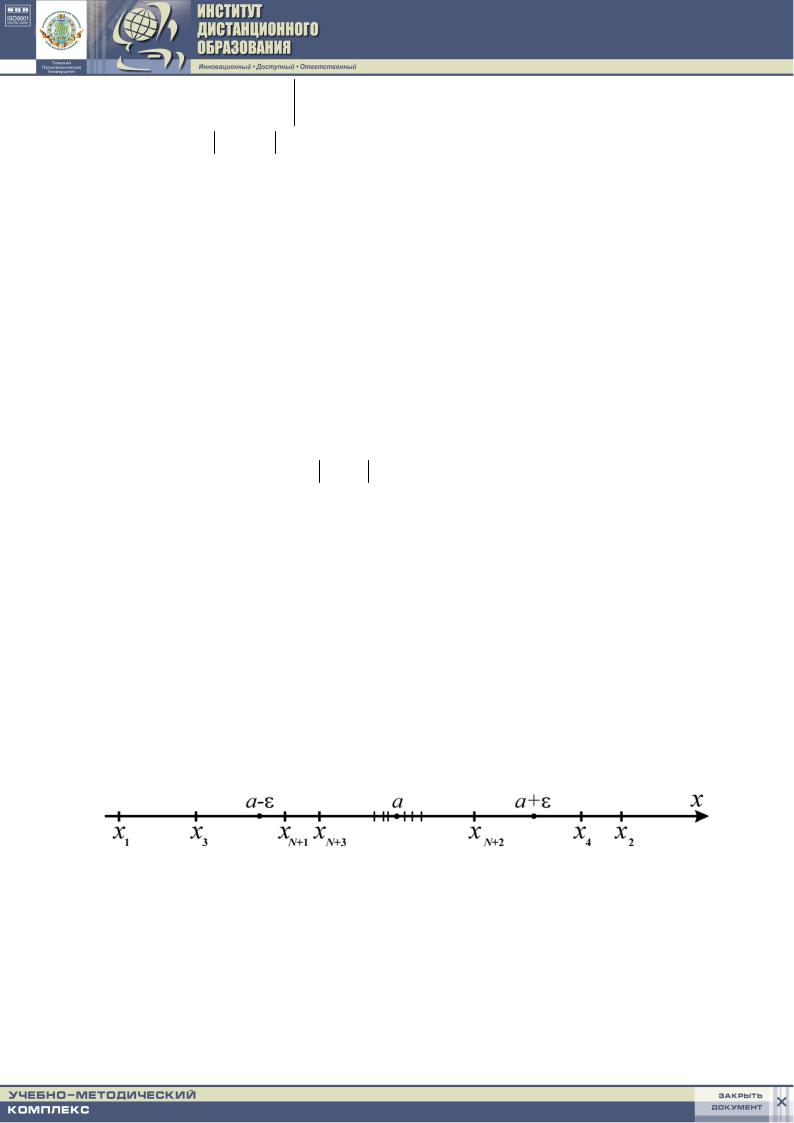
Изобразим числа a , a – ε, a + ε и значения переменной xn точками на

числовой оси (рис. 1). Выполнение неравенства (1.3) при условии n > N геометрически означает, что все точки xn , начиная с точки xN +1, то есть с точки,

индекс которой превосходит некоторое натуральное число N, будут непременно лежать в ε-окрестности точки а. Вне этой окрестности, если и будут находиться точки xn , то их окажется лишь конечное число.

Рис. 1

Признак сходимости монотонной последовательности

Теорема 1. Всякая невозрастающая (неубывающая) ограниченная снизу (сверху) последовательность {xn} или переменная величина xn имеет предел.

6

1.2. Бесконечно малые и бесконечно большие величины

Определение 1. Переменная величина xn называется бесконечно ма-

лой, если она имеет предел, равный нулю.

Следуя определению предела, можно сказать, что xn будет бесконечно

малой, если для любого сколь угодно малого ε > 0 найдется такое N, что для всех n > N выполняется неравенство xn <ε. Иначе говоря, бесконечно малой

называется такая переменная величина xn , которая при своём изменении, начиная с некоторого номера n, становится и остаётся по абсолютной величине меньше любого наперёд заданного числа ε > 0.

Пример 1. Доказать, что xn = (−n1)n есть бесконечно малая.

А это и значит, что xn = (−n1)n есть бесконечно малая.

Замечание 1. Нельзя смешивать постоянное очень малое число с бесконечно малой величиной. Единственным числом, которое рассматривается в качестве бесконечно малой величины, служит нуль (в силу того, что предел постоянной равен ей самой).

Определение 2. Переменная величина xn называется бесконечно

большой величиной, если для любого наперед заданного сколь угодно большого числа M > 0 можно указать такое натуральное число N, что для всех номеров n > N выполняется неравенство xn > М. Иначе говоря, переменная ве-

личина xn называется бесконечно большой, если, начиная с некоторого но-

мера, она становится и остаётся при всех последующих номерах по абсолютной величине больше любого наперед заданного положительного числа М.

О бесконечно большой переменной xn говорят, что она стремится к бесконечности или имеет бесконечный предел, и пишут:

7

В связи с введением нового понятия – «бесконечный предел» – условимся предел в ранее определенном смысле называть конечным пределом.

Пример 2. Величина xn = (−1)n n , принимающая последовательно значения -1, 2, -3, 4, -5, ..., (−1)n n, K – бесконечно большая.

Действительно, xn = (−1)n n = n . Отсюда ясно, что, каково бы ни было число М, для всех n, начиная с некоторого, будет xn = n > М, то есть

lim xn = ∞ .

n→∞

Определение 3. Переменная величина xn называется положительной

бесконечно большой величиной, если для любого числа М можно указать такое натуральное число N, что для всех номеров n > N выполняется неравенство xn > М.

В этом случае говорят, что переменная величина xn стремится к плюс бесконечности и символически записывают это так:

Определение 4. Переменная величина xn называется отрицательной

бесконечно большой величиной, если для любого числа М можно указать такое натуральное число N, что при всех n > N выполняется неравенство xn <М.

В этом случае говорят, что переменная величина xn стремится к минус бесконечности и записывают это так:

Так, например, xn = n будет положительной, а xn = −n – отрицательной

бесконечно большой величиной.

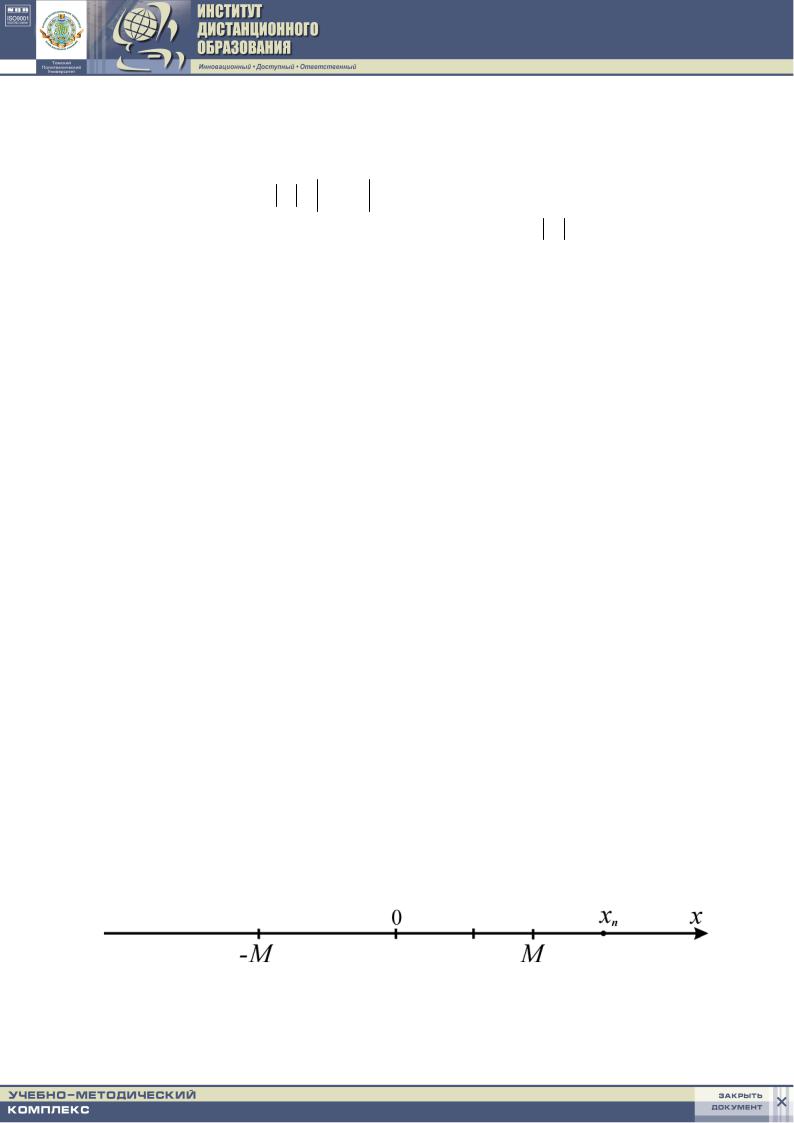
Переводя предыдущие определения на геометрический язык, мы можем сказать: если xn – бесконечно большая величина, то, как бы ни был велик

сегмент длины 2М (М > 0) с центром в начале координат, точка xn , изобра-

жающая значения бесконечно большой величины, при достаточно большом номере n окажется вне указанного сегмента и при дальнейшем увеличении n будет оставаться вне его (рис. 2). При этом, если xn – положительная (отри-

цательная) бесконечно большая величина, то точка, изображающая её значения, окажется для достаточно больших номеров n вне указанного сегмента с правой (левой) стороны от начала координат.

Рис. 2

8

Замечание 2.

1. Символы ∞, + ∞, −∞ не являются числами, а вводятся только для

упрощения записи и для сокращенного словесного выражения того факта, что переменная величина является бесконечно большой, положительной бесконечно большой и отрицательной бесконечно большой. Следует твердо запомнить, что никаких арифметических действий над этими символами производить нельзя!

2. Нельзя смешивать постоянное очень большое число с бесконечно большой величиной.

Связь между бесконечно большой и бесконечно малой величинами

Теорема 1. Пустьxn ≠0 (при любом n). Если xn – бесконечно большая, то yn =1/ xn – бесконечно малая; если xn – бесконечно малая, то yn =1/ xn – бесконечно большая.

1.3. Арифметические действия над переменными величинами. Основные теоремы о пределах переменных (последовательностей)

Введём понятие об арифметических операциях над переменными вели-

каждое значение которой равно сумме соответствующих (с одними и теми же номерами) значений переменных xn и yn , то есть переменную, прини-

мающую последовательность значений

x1 + y1, x2 + y2 , K, xn + yn , K

Мы будем обозначать эту переменную через xn + yn .

Аналогично определяется сумма любого числа переменных, их произведение, а также разность двух переменных и их частное.

Таким образом, возникают новые переменные:

xn + yn , xn − yn , xn yn и xn / yn .

(В последнем случае предполагается, что, хотя бы с некоторого номера yn ≠0, и частное xn / yn рассматривается только для таких номеров).

Аналогичным образом эти определения формулируются в терминах последовательностей.

9

Теоремы о пределах переменных Теорема 1. Переменная xn может иметь только один предел.

Между переменными величинами, имеющими предел, и бесконечно малыми величинами существует связь.

Теорема 2. Переменную величину, имеющую предел, можно представить в виде суммы своего предела и некоторой бесконечно малой величины.

Теорема 3 (обратная к теореме 2). Если переменную величину xn мож-

где а есть некоторое число, а αn – бесконечно малая, то а есть предел переменной величины xn .

Теорема 4. Если переменная xn имеет конечный предел, то она огра-

ничена.

Следствие. Бесконечно малая переменная ограничена.

Лемма 1. Алгебраическая сумма любого (но ограниченного) числа бесконечно малых величин есть также величина бесконечно малая.

Лемма 2. Произведение ограниченной переменной величины xn на бесконечно малую αn есть величина бесконечно малая.

Следствие 1. Произведение любого конечного числа бесконечно малых величин представляет собой бесконечно малую величину.

Следствие 2. Произведение постоянной величины на бесконечно малую есть величина бесконечно малая.

Следствие 3. Произведение переменной величины, стремящейся к пределу, на бесконечно малую есть величина бесконечно малая.

Пользуясьлеммами1 и2 можнодоказатьследующиетеоремыопределах. Теорема 5. Если переменные xn и yn имеют конечные пределы, то их

lim yn ≠ 0, тоичастноеэтихпеременныхтакжеимеетпредел, причем

n→∞

10