
- •1 Основные теоретические сведения
- •1.1.1 Прогнозирование и планирование как функция менеджмента
- •1.1.2 Обзор техники и видов планирования
- •1.1.3 Примеры планирования, на базе деловой компьютерной игры БК: Максимум
- •1.2 Методы макроэкономического планирования и прогнозирования
- •1.2.1 Организация прогнозирования и планирования
- •1.2.2 Федеральные целевые программы
- •2 Методы и модели в принятии управленческих решений
- •2.1 Принятие решений в условиях полной определенности
- •2.1.1 Многокритериальные методы оптимизации
- •2.2 Модели оценки социального и экономического развития регионов
- •3 Прогнозирование
- •3.1 Оценка и прогнозирование спроса
- •3.2 Оценка и прогнозирование спроса на основе экстраполяции
- •3.2.1 Прогнозирование с помощью абсолютных приростов
- •3.2.2 Прогнозирование с помощью относительных приростов
- •3.2.3 Прогнозирование с помощью индексов
- •3.2.4 Адаптивные методы прогнозирования
- •3.3 Оценка и прогнозирование спроса с помощью моделирования
- •3.3.1 Прогнозирование на основе трендовых моделей
- •3.3.2 Прогнозирование на основе однофакторных моделей
- •3.3.3 Прогнозирование с учетом сезонных эффектов
- •4 Основные разделы комплексного планирования (в рамках производственной программы)
- •4.1 Планирование подготовки производства
- •4.1.1 Планирование потребности в материалах
- •4.1.2 Планирование затрат на приобретение материалов
- •4.2 Планирование производственной программы
- •4.2.1 Детерминированные модели согласования объемов производства и спроса на продукцию предприятия
- •4.2.2 Расчет базовой цены товара
- •4.3 Прогнозирование и индикативное планирование развития комплексов, отраслей и сфер национальной экономики
- •4.3.2 Прогнозирование развития материального производства
- •4.3.3 Прогнозирование социального развития
- •4.3.4 Планирование доходов и расходов государства
- •4.3.5 Планирование производства в государственном секторе
- •5 Вопросы к зачету
- •Список использованных источников

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.2 II |
|
JJ |
3.3.2Прогнозирование на основе однофакторных моделей
Обычно на спрос влияют несколько факторов сразу. Отбор факторов и построение значимой многофакторной модели является непростой задачей. В упрощенном случае прогнозирование осуществляют с помощью однофакторных моделей. Данные модели могут давать вполне эффективный прогноз, если имеется главный (определяющий) фактор спроса. В частности, достаточно простое прогнозирование спроса может осуществляться на основе эластичности спроса.
Прогнозирование |
Стр. 92 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.2 II |
|
JJ |
Прогнозирование на основе эластичности. |
Эластично- |
стью произвольной функции f(x) по переменной x в точке x0
называется число |
x0 |
|
Ex(f ) = f 0(x0) · |
||
f(x0) |
(данная эластичность называется точечной, так как вычисляется в точке).
На практике часто используют другую формулу. Так для функции спроса Q(P) эластичность по цене P по определению
составляет
Ep(Q) = Qp0 · Qp .
Функциональная зависимость спроса, как правило, не известна, поэтому расчет осуществляют по формуле
Ep(Q) = |
|
Q/Q |
= |
Q |
· |
|
P |
, |
|
P/P |
P |
Q |
|||||
где P — изменение цены, |
Q — изменение объема спро- |
|||||||
са, вызванное изменением цены. Обычно в экономике говорят, что эластичность показывает на сколько процентов изменится функция (объем спроса) при изменении фактора (цены) на один процент. Это действительно так, если изменение цены P составляет один процент.
Возможен расчет еще по одной формуле (дуговой эластичности):
Eдуг. |
= Q2 − Q1 |
· |
|
P2 + P1 . |
||||
|
|
|
|
|
|
|
||
|
P2 |
− |
P1 |
Q2 + Q1 |
||||
|
|
|
|
|
|
|
|
|
где P1, Q1 — старое значение цены и объема спроса, P2, Q2
— новое значение цены и объема спроса. Формула дуговой эластичности в отличие от предыдущих формул рассчитывает среднее значение эластичности на дуге кривой спроса, определяемой значениями цен P1 и P2. Эту формулу рекомендуют использовать при значительном изменении цен, а в случае малых изменений — предыдущую.
Прогнозирование |
Стр. 93 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.2 II |
|
JJ |
Пример 3.3. В базовом периоде организация продала 505 единиц продукции по цене 9,8 ден. ед. В последнем периоде по цене 10 ден. ед. было продано продукция в объеме 485 единиц. Поэтому в целях расширения спроса организация запланировала снижение цены до 9,0 ден. ед. Требуется спрогнозировать какой объем спроса будет при такой цене.
Решение. Вычислим эластичность спроса по формуле дуговой эластичности:
Eдуг. |
= |
485 − 505 |
|
· |
10,0 + 9,8 |
= |
−20 |
· |
19,8 |
= |
− |
2. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
10,0 |
− |
9,8 |
485 + 505 |
|
0,2 |
|
990 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как предлагается снизить цену на 1 ден. ед. или на −10%, то в соответствии с эластичностью объем спроса изменится на (−2) · (−10%) = 20%, т. е. повысится на 20% и составит
485 · (1 + 0,20) = 582 (единиц).
Прогнозирование |
Стр. 94 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.2 II |
|
JJ |
Прогнозирование с помощью диаграмм MS Excel.
Пусть имеется один определяющий спрос фактор. Для оценки характера влияния этого фактора и прогнозирования спроса можно использовать диаграмму типа «Точечная». Достаточно построить график (точечной) зависимости объема спроса y от значений фактора x. Характер расположения точек на графике покажет наличие связи между фактором спроса и объемом спроса, а также направление и силу связи. Более точную информацию можно получить после добавления различных линий тренда и вывода уравнений трендов и степени их аппроксимации. По уравнению наилучшего тренда могут быть вычислены прогнозы спроса в зависимости от прогнозных (или планируемых) значений фактора.
Для построения однофакторных моделей можно использовать четыре типа трендов:
•y = a + bx — линейный,
•y = a · xb — степенной,
•y = a · ebx — экспоненциальный,
•y = a + b ln x — логарифмический.
Коэффициент детерминации R2 моделей показывает на сколько стабильно влияния фактора, а уравнение тренда показывает вид этой зависимости.
Прогнозирование |
Стр. 95 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.2 II |
|
JJ |
Если значение R2 близко к единице, то в наблюдаемом периоде влияние фактора на спрос оставалось неизменным. В частности:
•в линейной модели параметр b указывает на сколько в среднем менялся объем спроса y при изменении фактора x на единицу;
•в степенной модели параметр b указывает на сколько процентов в среднем менялся объем спроса y при изменении фактора x на один процент, т. е. показатель степени в степенной модели указывает на эластичность влияния фактора.
Для линейной модели y = a + bx среднее значение эластичности влияния фактора x также легко найти:
Ex(y) = b · x0 , y0
где x0 и y0 — средние значения фактора x и результативного показателя y (определяются на основе наблюдений).
На практике форма зависимости должна быть известна заранее либо выбор типа тренда определяется по максимальному значению коэффициента детерминации R2. Две факторные модели считаются одинакового качества по степени аппроксимации, если их коэффициенты детерминации отличаются приблизительно менее чем на5 0,05.
5Различие в менее чем менее 5% можно «списать» на статистическую ошибку. Более точный диагноз осуществляется путем проверки соответствующей статистической гипотезы [?].
Прогнозирование |
Стр. 96 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.2 II |
|
JJ |
Пример 3.4. Известны данные об объемах потребления мяса цыплят, среднего уровня дохода потребителей, цены мяса цыплят, мяса говядины и свинины в течение 20 периодов (лет) (табл. 3.2). Требуется отобрать наиболее существенный фактор, наилучшую однофакторную модель потребления мяса цыплят и с помощью нее спрогнозировать объем потребления мяса цыплят на последующие четыре года. Прогнозные значения фактора рассчитать с помощью трендовой модели.
Таблица 3.2. Данные о потреблении, доходах и ценах
|
Период, |
Потреб- |
Доход, |
Цена |
|
Цена |
Цена |
|
|
||
|
год |
ление, |
ден. ед. |
цыплят, |
|
говядины, |
свинины, |
|
|
||
|
усл. ед. |
ден. ед. |
|
ден. ед. |
ден. ед. |
|
|
||||
|
|
|
|
|
|
||||||
|
t |
y |
x1 |
x2 |
|
|
x3 |
x4 |
|
|
|
|
1 |
30,8 |
459,7 |
39,5 |
|
55,3 |
79,2 |
|
|
||
|
2 |
31,2 |
492,9 |
37,3 |
|
54,7 |
77,4 |
|
|
||
|
3 |
33,3 |
528,6 |
38,1 |
|
63,7 |
80,2 |
|
|
||
|
4 |
35,6 |
560,3 |
39,3 |
|
69,8 |
80,4 |
|
|
||
|
5 |
36,4 |
624,6 |
37,8 |
|
65,9 |
83,9 |
|
|
||
|
6 |
36,7 |
666,4 |
38,4 |
|
64,5 |
85,5 |
|
|
||
|
7 |
38,4 |
717,8 |
40,1 |
|
70,0 |
93,7 |
|
|
||
|
8 |
40,4 |
768,2 |
38,6 |
|
73,2 |
106,1 |
|
|
||
|
9 |
40,3 |
843,3 |
39,8 |
|
67,8 |
104,8 |
|
|
||
|
10 |
41,8 |
911,6 |
39,7 |
|
79,1 |
114,0 |
|
|
||
|
11 |
40,4 |
931,1 |
52,1 |
|
95,4 |
124,1 |
|
|
||
|
12 |
40,7 |
1021,5 |
48,9 |
|
94,2 |
127,6 |
|
|
||
|
13 |
40,1 |
1165,9 |
58,3 |
|
123,5 |
142,9 |
|
|
||
|
14 |
42,7 |
1349,6 |
57,9 |
|
129,9 |
143,6 |
|
|
||
|
15 |
44,1 |
1449,4 |
56,5 |
|
117,6 |
139,2 |
|
|
||
|
16 |
46,7 |
1575,5 |
63,7 |
|
130,9 |
165,5 |
|
|
||
|
17 |
50,6 |
1759,1 |
61,6 |
|
129,8 |
203,3 |
|
|
||
|
18 |
50,1 |
1994,2 |
58,9 |
|
128,0 |
219,6 |
|
|
||
|
19 |
51,7 |
2258,1 |
66,4 |
|
141,0 |
221,6 |
|
|
||
|
20 |
52,9 |
2478,7 |
70,4 |
|
168,2 |
232,6 |
|
|
||
Прогнозирование |
Стр. 97 из 164 |
|
J I |
|
J I x y |
× |
|||||
|
|
||||||||||
|
|
|
10 |
|
41,8 |
|
911,6 |
|
|
|
39,7 |
|
79,1 |
|
114 |
3.3.2 |
II |
||
Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
|||||||||||||||||||
|
|
|
11 |
|
40,4 |
|
931,1 |
|
|
|
52,1 |
|
95,4 |
124,1 |
|
|
|||
|
|
Решение12 |
.40,7Согласно1021,5алгоритму,48,9 |
указанному94,2 127,6выше, построим JJ |
|||||||||||||||
|
|
|
13 |
|
40,1 |
|
1165,9 |
|
|
|
58,3 |
|
123,5 |
142,9 |
|
|
|
||
точечную диаграмму зависимости объема потребления y от зна- |
|
||||||||||||||||||
|
|
|
14 |
|
42,7 |
|
1349,6 |
|
|
|
57,9 |
|
129,9 |
143,6 |
|
|
|
||
чений дохода x1 |
и добавим к диаграмме четыре тренда: линей- |
|
|||||||||||||||||
|
|
|
15 |
|
44,1 |
|
1449,4 |
|
|
|
56,5 |
|
117,6 |
139,2 |
|
|
|
||
ный, экспоненциальный, логарифмический и степенной. В пара- |
|
||||||||||||||||||
|
|
|
16 |
|
46,7 |
|
1575,5 |
|
|
|
63,7 |
|
130,9 |
165,5 |
|
|
|
||
|
|
|
17 |
|
50,6 |
|
1759,1 |
|
|
|
61,6 |
|
129,8 |
203,3 |
|
|
|
||
метрах каждого тренда укажем вывод уравнения тренда и сте- |
|
||||||||||||||||||
|
|
|
18 |
|
50,1 |
|
1994,2 |
|
2 |
. |
58,9 |
|
128 |
219,6 |
|
|
|
||
пень его аппроксимации R |
|
В результате получим диаграмму |
|
||||||||||||||||
|
|
|
19 |
|
51,7 |
|
2258,1 |
|
|
|
66,4 |
|
141 |
221,6 |
|
|
|
||
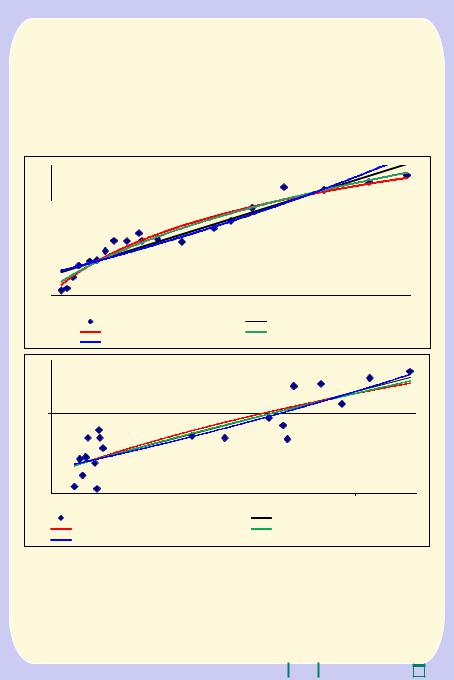
как на рисунке 3.3. |
2478,7 |
|
|
|
70,4 |
|
168,2 |
232,6 |
|
|
|
||||||||
|
|
|
20 |
|
52,9 |
|
|
|
|
|
|
|
|
||||||
55 |
|
y = 24,56ln(x) - 53,81 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рис. 3.3. Модели влияния дохода на объем потребления мяса цыплят |
|
||||||||||||||||||
50 |
|
|
R² = 0,739 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y = 22,82e0,011x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
R² = 0,726 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
45Среди полученных моделей наилучшей оказалась логариф- |
|
||||||||||||||||||
мическая — R |
2 |
= 0,9495. |
|
|
|
|
|
|
|
y = 0,494x + 16,93 |
|
||||||||
|
Степенная модель получилась прак- |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
R² = 0,752 |
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
= 0,9418. |
С экономической0,588 |
|
|||||
тически такого же качества — R |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = 4,184x |
|
|
|
точки зрения удобнее использовать степенную модель,R² = 0,719 так как |
|
||||||||||||||||||
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получаем интерпретацию влияния дохода в терминах эластично- |
|
||||||||||||||||||
стей:30 с ростом дохода на 10% потребление мяса цыплят растет |
|
||||||||||||||||||
на |
|
35 |
40 |
|
|
|
|
50 |
|
|
55 |
60 |
65 |
|
70 |
|
|||
0, |
2945 10% = 2,945%. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Х1·доход |
|
|
|
|
|
|
|
Линейная зависимость |
|
|
|
||||||
|
|
Положительное значение эластичности влияния дохода на |
|
||||||||||||||||
|
|
|
|
Логарифмическая (Х1 доход) |
|
|
Степенная зависимость |
|
|
|
|||||||||
|
|
|
|
Экспонен. зависимость |
|
|
|
|
|
|
|
|
|
|
|
||||
объем потребления означает, что мясо цыплят является нор- |
|
||||||||||||||||||
мальным товаром (рост доходов приводит к росту потребле- |
|
||||||||||||||||||
ния). В то же время, это значение эластичности меньше еди- |
|
||||||||||||||||||
ницы (0,2945 < 1), поэтому данный продукт можно отнести к |
|
||||||||||||||||||
товарам первой необходимости (а, значит, ценовые факторы не |
|
||||||||||||||||||
должны существенно влиять на объем потребления). |
|
|
|
||||||||||||||||
Прогнозирование |
|
|
|
Стр. 98 из 164 |
J I J I x y |
× |
|||||||||||||

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.2 II |
|
JJ |
Среди четырех построенных моделей экспоненциальную модель можно рассматривать как более низкого качества, так как у нее коэффициент детерминации R2 = 0,8733 существенно меньше коэффициента детерминации логарифмической модели (более чем на 0,05).
Следовательно, для прогнозирования объема потребления могут быть использованы логарифмическая, степенная и линейная модели. На рисунке 3.3 видно, что логарифмическая модель дает более пессимистический прогноз, линейная — наиболее оптимистический прогноз, а степенная модель — промежуточный (наиболее вероятный).
Линейная модель также может использоваться для экономической интерпретации влияния дохода на объем потребления мяса цыплят: в исследуемом периоде с ростом дохода на 100 ден. ед. потребление в среднем росло на 0,010 · 100 = 1,0 усл. ед.
Для прогнозирования объема потребления мяса цыплят на ближайшие четыре года необходимо знать значения дохода потребителей в прогнозируемом периоде. Эти данные могут быть получены на основе экспертных оценок. Например, в зависимости от состояния внешней (мировой) и внутренней конъюнктуры эксперты дают прогноз о возможном росте или падении ВВП страны (в относительных показателях). Эти оценки также можно рассматривать как прогноз динамики средних доходов населения страны.
В нашем случае экспертных оценок о динамике дохода нет. Поэтому будем считать, что экономическая конъюнктура сохра-
нится и рассчитаем прогноз дохода на основе трендовых моделей6.
6В условиях сохраняющейся конъюнктуры проще прогнозировать на основе экстраполяции с помощью трендовых моделей. Использование факторных моделей эффективно при наличии экспертных оценок об изменении конъюнктуры важнейших факторов спроса.
Прогнозирование |
Стр. 99 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.2 II |
|
JJ |
На основе трендовых моделей, реализованных в MS Excel, |
|
получаем, что наилучшей является экспоненциальная |
модель |
y = 392, 6e0,087x, где x — период (год), с R2 = 0,99. Модель показывает, что в среднем каждый год доходы населения росли с темпом 0,087 или 8,7%. С учетом эластичности влияния дохода получаем, что ежегодно будет расти потребление мяса цыплят на 8,7% · 0,2945 ≈ 2,56%.
Таким образом, на основе эластичности получаем следующие прогнозы потребления мяса цыплят: в 21 году — 54,3 усл. ед., в 22 году — 55,6 усл. ед., в 23 году — 57,1 усл. ед. и в 24 году — 58,5 усл. ед.
Более точное значение объема потребления получаем на основе факторных моделей (табл. 3.3).
Таблица 3.3. Прогнозы потребления в зависимости от влияния дохода
Год |
Доход, ден. ед. |
Потребление, усл. ед., y = |
||
t |
x1 = 392,6e0,087t |
12,188 ln x1 − 42,81 |
5,3465x10,2945 |
0,010x1 + 29,69 |
21 |
2440,1 |
52,3 |
53,2 |
54,1 |
22 |
2661,9 |
53,3 |
54,5 |
46,3 |
23 |
2903,8 |
54,4 |
56,0 |
58,7 |
24 |
3167,8 |
55,4 |
57,4 |
61,4 |
Прогнозирование |
Стр. 100 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.2 II |
|
JJ |
Для расчета различных прогнозов потребления мяса цыплят сначала были вычислены прогнозы дохода в 21–24 периодах (годах) по экспоненциальной модели x1 = 392,6e0,087t. В частности, прогноз на 21 год был вычислен в Excel по формуле
=392,6*exp(0,087*21).
Прогноз потребления на 21 год на основе логарифмической модели y = 12,188 ln x1 − 42,81 рассчитан в Excel по формуле =12,188*ln(2440,1)-42,81. Аналогичным образом были вычислены прогнозы потребления в 21–24 годах по всем моделям.
Наиболее вероятное значение роста потребления описывается степенной моделью: потребление в 21–24 годах будет расти от 53,2 до 57,4 усл. ед. Этот прогноз потребления оказалсся меньше на 1,1 усл. ед. чем при прогнозировании на основе эластичности и на 0,4–0,5 усл. ед. меньше чем при прогнозировании на основе трендовой (экспоненциальной) модели.
Для построения различных однофакторных моделей объема потребления мяса цыплят в зависимости от их цены достаточно сделать копию предыдущего графика. На копии нужно щелкнуть курсором «мышки» по точке графика потребления. В результате в таблице Excel с помощью двух цветных прямоугольников будут выделены исходные данные потребления мяса цыплят y и доход потребителей x1. Далее нужно «взять» за край (левой кнопкой «мышки») прямоугольник с данными x1 и «перетащить» его к данным x2. В итоге будет получен точечный график зависимости y от x2, четыре тренда к нему, уравнения трендов и степени аппроксимаций этих трендов как на рисунке7 3.4.
7Такое свойство диаграмм выполняется, если не было «ручного» редактирования отдельных параметров диаграммы. Например, после изменения цвета, которым было написано уравнение тренда, смена исходных данных (фактора) не приводит к изменению уравнения тренда.
Прогнозирование |
Стр. 101 из 164 |
|
J I |
|
J I x y × |
|
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
JJ |
55 |
y = 24,56ln(x) - 53,81 |
|
|
|
|
|
|
|
|
|
|
|
|
||
50 |
R² = 0,739 |
|
|
|
|
|
|
y = 22,82e0,011x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
R² = 0,726 |
|
|
|
|
|
|
|
|
|
|
|
y = 0,494x + 16,93 |
||
|
|
|
|
|
|
||
40 |
|
|
|
|
|
R² = 0,752 |
|
|
|
|
|
|
y = 4,184x0,588 |
|
|
|
|
|
|
|
|
|
|
35 |
|
|
|
|
|
R² = 0,719 |
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
|
Х1 доход |
|
|
|
Линейная зависимость |
|
|
|
Логарифмическая (Х1 доход) |
|
Степенная зависимость |
|
|||
|
Экспонен. зависимость |
|
|
|
|
|
|
|
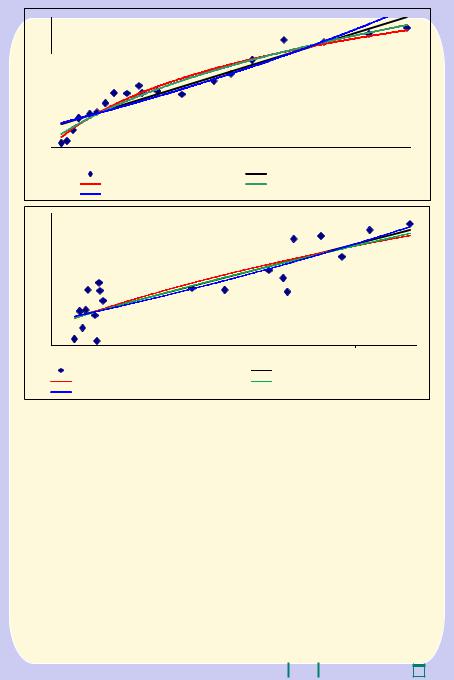
Рис. 3.4. Модели влияния цены мяса цыплят на объем |
|
|||||
|
его потребления |
|
|
|
|
||
Прогнозирование |
|
Стр. 102 из 164 J I |
J I x y |
× |
|||

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.2 II |
|
JJ |
Все полученные уравнения трендов имеет примерно одинаковое качество, которое значительно ниже чем у моделей с фактором x1. Таким образом, влияние цены на объем потребления мяса цыплят существенно слабее чем влияние дохода. Данный вывод подтверждает и графический анализ. В частности, все наблюдения можно разделить на три группы. В левой части рисунка 3.4 сосредоточены результаты наблюдений, показывающие рост потребления с 30 до 42 усл. ед. при относительно стабильных ценах (в пределах от 37 до 40 ден. ед.). В центральной части наблюдается существенный рост цены (с 40 до 58 ден. ед.) и небольшое снижение потребления. В правой части растет объем потребления при разнонаправленном изменении цен. Все это указывает на относительно слабую связь между ценой мяса цыплят и его потреблением.
Аналогичным образом может быть проведен анализ влияния оставшихся факторов. В целом цена мяса говядины влияет на объем потребления существенно ниже чем доход, а влияние цены мяса говядины на потребление почти такое же как у дохода. С экономической точки зрения не имеет смысла рассматривать влияние цен товаров-заменителей, если цена самого товара оказывается несущественным фактором. Сильное влияние цены мяса свинины на потребление мяса цыплят требует дополнительного анализа. В частности, это объясняется очень сильной корреляционной связью между ценой мяса свинины и доходами потребителей.
Прогнозирование |
Стр. 103 из 164 |
|
J I |
|
J I x y × |
|
|
