
- •1 Основные теоретические сведения
- •1.1.1 Прогнозирование и планирование как функция менеджмента
- •1.1.2 Обзор техники и видов планирования
- •1.1.3 Примеры планирования, на базе деловой компьютерной игры БК: Максимум
- •1.2 Методы макроэкономического планирования и прогнозирования
- •1.2.1 Организация прогнозирования и планирования
- •1.2.2 Федеральные целевые программы
- •2 Методы и модели в принятии управленческих решений
- •2.1 Принятие решений в условиях полной определенности
- •2.1.1 Многокритериальные методы оптимизации
- •2.2 Модели оценки социального и экономического развития регионов
- •3 Прогнозирование
- •3.1 Оценка и прогнозирование спроса
- •3.2 Оценка и прогнозирование спроса на основе экстраполяции
- •3.2.1 Прогнозирование с помощью абсолютных приростов
- •3.2.2 Прогнозирование с помощью относительных приростов
- •3.2.3 Прогнозирование с помощью индексов
- •3.2.4 Адаптивные методы прогнозирования
- •3.3 Оценка и прогнозирование спроса с помощью моделирования
- •3.3.1 Прогнозирование на основе трендовых моделей
- •3.3.2 Прогнозирование на основе однофакторных моделей
- •3.3.3 Прогнозирование с учетом сезонных эффектов
- •4 Основные разделы комплексного планирования (в рамках производственной программы)
- •4.1 Планирование подготовки производства
- •4.1.1 Планирование потребности в материалах
- •4.1.2 Планирование затрат на приобретение материалов
- •4.2 Планирование производственной программы
- •4.2.1 Детерминированные модели согласования объемов производства и спроса на продукцию предприятия
- •4.2.2 Расчет базовой цены товара
- •4.3 Прогнозирование и индикативное планирование развития комплексов, отраслей и сфер национальной экономики
- •4.3.2 Прогнозирование развития материального производства
- •4.3.3 Прогнозирование социального развития
- •4.3.4 Планирование доходов и расходов государства
- •4.3.5 Планирование производства в государственном секторе
- •5 Вопросы к зачету
- •Список использованных источников

Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.3 II |
|
JJ |
3.2.3 Прогнозирование с помощью индексов
При наличии линейно-мультипликативноого тренда более точное прогнозирование предполагает применение цепных индексов и расчет их среднего геометрического значения. Обо-
значим цепной индекс в период t через qt = dt . Постоянство dt−1
темпов прироста означает, что ряд {qt} состоит из одинаковых элементов, значение которых отличается от темпа прироста на единицу. Прогноз на основе цепных индексов осуществляется следующим образом. Сначала вычисляются цепные индексы qt, t = 2, 3, . . . , n, и их среднее геометрическое значение
r
q = n−√1 q2q3 . . . qn = n−1 dn . d1
Тогда прогноз ˆn+1 в период получается путем умноже- d t = n+1
ния последнего значения dn на среднее геометрическое значение q цепного индекса (в MS Excel можно использовать функцию
СРГЕОМ):
ˆ |
= dn · q. |
(3.5) |
dn+1 |
Для прогнозирования на k периодов вперед необходимо среднее геометрическое значение индекса возвести в степень k:
ˆ |
k |
. |
(3.6) |
dn+k = dn · q |
|
Чем дальше будет строиться такой прогноз, тем он будет менее надежным. Для повышения надежности нужно учитывать вновь поступающую информацию и корректировать прогноз.
Прогнозирование по формулам (3.5) и (3.6) называют индексным методом.
Прогнозирование |
Стр. 69 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.4 II |
|
JJ |
3.2.4 Адаптивные методы прогнозирования
Рассмотрим наиболее простые адаптивные методы экстраполяции временных рядов: на базе скользящего среднего и экспоненциального сглаживания. Данные методы предполагают, что исходный временной ряд не имеет тенденции и устойчивых циклических (сезонных) колебаний. В противном случае из временного ряда необходимо предварительно исключить тренд и сезонные колебания. Для комбинированного ряда итоговый прогноз складывается из нескольких прогнозов: по тренду, сезонной компоненте и прогнозного значения остаточной компоненты, полученного с помощью скользящей средней, экспоненциального среднего или иных методов.
Прогнозирование |
Стр. 70 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.4 II |
|
JJ |
Скользящее среднее. Формально простое скользящее среднее mt определяется как среднее арифметическое k последних наблюдений:
mt = |
|
сумма последних k наблюдений |
|
|
t−(k−1) |
|||||
|
− |
− |
|
t− k− = |
Pi t . |
|||||
|
z |
|
|
}| |
|
{ |
|
di |
||
|
dt + dt 1 + dt 2 + . . . + d ( 1) |
|
= |
|
||||||
|
|
|
|
|
k |
|
|
|
k |
|
Число k — характеризует степень сглаживания — число точек, учитывающихся при расчете средних значений. Чем больше значение k, тем менее чувствительно скользящее среднее к колебаниям ряда {dt}.
В качестве прогнозного значения yˆt+1 в период t + 1 может быть использован показатель mt. Так формула скользящего среднего может быть переписана в следующем виде:
ˆ |
= |
mt |
= |
mt−1 |
+ |
dt − dt−k |
= ˆ |
+ |
dt |
− |
dt−k |
. |
|
k |
|||||||||||||
yt+1 |
|
|
|
k |
yt |
|
k |
||||||
Это означает, что метод скользящего среднего прогнозирует на основании среднего значения последних k наблюдений (значений спроса) и этот прогноз каждый раз корректируется с учетом поступающей информации: новое прогнозное значение равно старому прогнозу плюс корректировка — последнее значение объема спроса dt за вычетом устаревшего спроса k периодов назад dt−k с весом 1k.
Прогнозирование |
Стр. 71 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.4 II |
|
JJ |
Вычисление скользящих средних значений удобно производить в Excel. Для этого достаточно вычислить только одно значение скользящего среднего и воспользоваться процедурой «протягивания» формулы. Кроме этого в Excel имеются специальные возможности: в пакете «Анализ данных» имеется режим «Скользящее среднее», позволяющий вычислять скользящие средние. В качестве параметра «Интервал» необходимо указывать шаг сглаживания (значение параметра k). Дополнительно график скользящей средней можно добавлять к исходному графику как тренд «Линейная фильтрация».
Самый популярный подход к использованию процедур сглаживания для прогнозирования состоит в сравнении взаимного расположения графиков скользящей средней и исходных данных. Если кривая скользящей средней находится ниже кривой исходных данных, то преобладает тенденция к повышению; если выше — преобладает тенденция к понижению. Пересечение графиков скользящей средней и исходных данных указывает на изменение направленности тренда. Данный сигнал говорит о том, что пора принимать соответствующее решение, так как происходит изменение направления общей тенденции. В частности, если исходные данные характеризуют объемы спроса в различные периоды, то пересечение скользящей средней с кривой спроса сверху вниз указывает на то, что происходит смена тенденции снижения спроса на тенденцию повышения спроса.
Прогнозирование |
Стр. 72 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.4 II |
|
JJ |
Для анализа рыночных трендов часто используют комбинации скользящих средних. Например, если короткая скользящая средняя находится выше более длинной, то это подтверждает тенденцию к понижению. Важная задача состоит в определении оптимального параметра сглаживания k. Чем больше этот параметр, тем сильнее запаздывают сигналы, а чем короче — тем больше появляется ложных сигналов. Целесообразно выбирать длину интервала сглаживания в зависимости от того, на какой промежуток времени требуется получить прогноз спроса. Для конкретных рынков параметр k скользящих средних определяют эмпирическим путем.
Прогнозирование |
Стр. 73 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.4 II |
|
JJ |
Метод скользящего среднего применяют не только для прогнозирования общей тенденции. Например, с помощью данной процедуры можно сгладить сезонные (циклические) колебания. Тогда, если из исходного ряда вычесть сглаженный ряд, то будет получено влияние только сезонных (циклических) и случайных воздействий. В другом случае, сглаживание временного ряда позволяет уточнить экономическую сущность процесса. Пусть, например, временной ряд отражает объем отгрузки готовой продукции. Для крупного предприятия такие данные обычно имеют достаточно большие колебания, что затрудняет осуществлять прогнозирование и планирование деятельности. Причиной неравномерности объемов отгрузки может являться специфика оптового спроса и отгрузки, вызванная наличием запасов товаров в розничной торговле. Сглаживание исходного ряда позволяет найти величину розничного спроса. Оптимальный шаг сглаживания может устанавливаться на основе среднего срока хранения продукции в розничной торговле.
В рассмотренном методе для расчета средних значений учитываются одинаково последние k наблюдений, а на практике наибольшее влияние оказывают самые последние наблюдения. Этот недостаток устраняется путем введения весовых коэффициентов при вычислении средних значений. Другой недостаток
— частичная потеря информации на концах временного ряда — устраняется, например, с помощью прогнозирования на основе средних абсолютных приростов.
Рассмотренный метод скользящего среднего называют линейным сглаживанием, так как в нем для нахождения среднего (сглаженного) значения используются одинаковые весовые коэффициенты. В общем случае весовые коэффициенты могут быть различными (при нелинейном сглаживании) [5].
Возможны и иные методы сглаживания.
Прогнозирование |
Стр. 74 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.4 II |
|
JJ |
Экспоненциальное сглаживание. Принцип экспоненциального сглаживания заключается в том, что при вычислении экспоненциально среднего значения ut в период t учитываются все прошлые наблюдения d1, d2, . . . , dt, при этом вес наблюдения становится тем меньше, чем дальше в прошлое отстоит показатель. Данные веса распределяются по экспоненциальному закону (отсюда и название сглаживания).
Простое экспоненциально взвешенное среднее может быть определено по следующей формуле:
ut = (1 − α)ut−1 + αdt,
где α [0; 1] — параметр сглаживания.
В качестве прогнозного значения ˆt+1 в период может d (t + 1)
быть использовано значение2 ut. Из формулы экспоненциально среднего взвешенного следует, что такой метод прогнозирования носит адаптивный характер: учитывается значение прошлого прогноза ut−1 с весом (1−α) и последнее фактическое значение dt с весом α. Чем ближе α к нулю, тем сильнее учитываются прошлые значения и слабее последние; чем ближе α к единице, тем сильнее учитываются самые последние значения. Другими словами, чем больше α, тем чувствительнее модель к последним показателям.
2Эта методика может применяться и для прогнозированию на τ шагов впе-
ˆ |
− α)ut−1 |
+ αdt. |
ред: dt+τ = ut, где ut = (1 |
Прогнозирование |
Стр. 75 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.4 II |
|
JJ |
В отличие от скользящего среднего в данном методе достаточно задать лишь начальную точку для прогноза. В качестве начальной точки может быть, например, d1 или среднее значение всех показателей спроса d1, . . . , dn. Дальнейшее прогнозирование осуществляется при поступлении новых данных и не нужно заново производить вычисления, как это делалось при скользящем среднем.
На практике для стационарного ряда (т. е. не содержащего тенденции) рекомендуется выбирать значения α [0,05; 0,3], традиционное значение α = 0,2. Когда прогноз строится для нового товара, предпочтительнее брать более высокое значение α, чтобы учитывать свежую реакцию покупателей на новый товар [8].
Вычисление экспоненциально взвешенного среднего также как и скользящего среднего можно осуществлять в Excel по приведенной формуле. Для этого достаточно один раз набрать эту формулу и потом «протянуть». Возможно также воспользоваться в пакете «Анализ данных» режимом «Экспоненциальное сглаживание». В меню этого режима в окне «Фактор затухания» нужно указать значение α из промежутка [0; 1] (или рекомендуемого [0,05; 0,3]).
Прогнозирование |
Стр. 76 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.4 II |
|
JJ |
Пример 3.1. Имеются данные об объемах спроса на продукцию предприятия в течение 10 периодов (табл. 3.1, ячейки A1:B11). Требуется спрогнозировать объем спроса на ближайшие три периода в соответствии с различными методами прогнозирования:
а) линейно-аддитивного тренда (методом абсолютных приростов) по формуле (3.1) или (3.2);
б) линейно-мультипликативного тренда (методом относительных приростов) по формуле (3.3) или (3.4);
в) линейно-мультипликативного тренда (индексным методом) по формуле (3.5) или (3.6);
г) скользящего среднего с шагом сглаживания, равным 3; д) экспоненциального сглаживания с параметром α = 0,2; е) среднего арифметического всех полученных прогнозов.
Решение. На основе исходных данных (ячейки A2:B11 табл. 3.1) в столбце C вычислены абсолютные приросты объема спроса, средний абсолютный прирост вычислен в строке 12, а прогноз спроса в 11–13 периодах вычислен в 14–16 строках. Так в ячейке C3 введена формула =B3-B2 и «протянута» до ячейки C11. В ячейке C12 найдено среднее значение абсолютного прироста по формуле =СРЗНАЧ(C3:C11). На основе абсолютных приростов по формуле (3.1) рассчитан прогноз в 11 периоде:
=B11+$C$12.
Таким же образом найдены прогнозные значения спроса в 12 и 13 периодах — в ячейке C15 введена формула =C14+$C$12 и протянута до ячейки C16.
Прогнозирование |
Стр. 77 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.4 |
Таблица 3.1. Прогнозирование временного ряда
|
A |
B |
C |
D |
|
E |
F |
G |
|
|
Объем |
Абсолют- |
Относи- |
|
|
Скольз. |
Экспоненц. |
|
|
|
|
|||||
|
|
спро- |
ные |
тельные |
|
|
среднее, |
сглаживание, |
1 |
t |
са, y |
приросты |
приросты |
|
Индексы |
k = 3 |
α= 0,2 |
2 |
1 |
509,0 |
|
|
|
|
|
512,8 |
3 |
2 |
510,5 |
1,50 |
0,003 |
1,003 |
|
512,0 |
|
|
|
|
|
|
|
|
|
|
4 |
3 |
511,4 |
0,90 |
0,002 |
1,002 |
|
511,7 |
|
5 |
4 |
510,3 |
−1,10 |
−0,002 |
0,998 |
510,3 |
511,6 |
|
6 |
5 |
513,5 |
3,20 |
0,006 |
1,006 |
510,7 |
511,4 |
|
7 |
6 |
514,5 |
1,00 |
0,002 |
1,002 |
511,7 |
511,8 |
|
8 |
7 |
514,0 |
−0,50 |
−0,001 |
0,999 |
512,8 |
512,3 |
|
9 |
8 |
515,4 |
1,40 |
0,003 |
1,003 |
514,0 |
512,7 |
|
10 |
9 |
513,5 |
−1,90 |
−0,004 |
0,996 |
514,6 |
513,2 |
|
11 |
10 |
515,5 |
2,00 |
0,004 |
1,004 |
514,3 |
513,3 |
|
12 |
В среднем |
0,72 |
0,001 |
1,001 |
α = |
0,2 |
||
13 |
|
|
|
|
|
Прогноз |
|
|
14 |
11 |
|
516,2 |
516,2 |
|
516,2 |
514,8 |
513,7 |
15 |
12 |
|
516,9 |
517,0 |
|
517,0 |
514,6 |
|
16 |
13 |
|
517,7 |
517,7 |
|
517,7 |
515,0 |
|
II JJ
Прогнозирование |
Стр. 78 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.4 II |
|
JJ |
В столбце D произведены аналогичные расчеты относительных приростов и прогнозов. Так в ячейке D3 введена формула =C3/B2 (для вычисления относительного прироста), а в ячейке D12 — среднее значение относительного прироста — =СРЗНАЧ(D3:D11). На основе относительных приростов по формуле (3.3) рассчитан прогноз в 11 периоде:
=B11+$B$11*$D$12.
Таким же образом найдены прогнозные значения спроса в 12 и 13 периодах — в ячейке D15 введена формула =D14+$B$11*$D$12 и протянута до ячейки D16.
В столбце E вычислены цепные индексы и на их основе прогнозы. Так в ячейке E3 введена формула =B3/B2 (для вычисления цепного индекса), а в ячейке E12 среднее значение цепного индекса — =СРГЕОМ(E3:E11). На основе индексов по формуле (3.5) рассчитан прогноз в 11 периоде:
=B11*$E$12.
Таким же образом найдены прогнозные значения спроса в 12 и 13 периодах — в ячейке E15 введена формула =E14*$E$12 и протянута до ячейки E16.
В столбце F вычислены скользящие средние. Для установления соответствия между прогнозными значениями и прогнозируемыми периодами все расчеты смещены на одну ячейку вниз. Так в ячейке F5 вычисляется прогнозное значение в периоде t = 4 по формуле =СРЗНАЧ(B2:B4). Эта формула протянута до ячейки F11. Прогнозное значение в 11 периоде вычислено в ячейке F14 по формуле =СРЗНАЧ(B9:B11). Для прогнозирования спроса в 12 и 13 периодах исходных данных нет, вместо них используются прогнозные значениями и поэтому в ячейках F15 и F16 формулы изменены. Так в ячейке F15 введено
=(B10+B11+F14)/3, а в ячейке F16 — =(B11+F14+F15)/3.
Прогнозирование |
Стр. 79 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.4 II |
|
JJ |
В столбце G вычислены экспоненциально взвешенные средние с параметром α = 0,2 (которое введено в ячейке G12). Как и в предыдущем случае все расчеты сдвинуты на единицу вниз, чтобы прогноз соответствовал прогнозному периоду. В ячейке G2 введена формула =СРЗНАЧ(B2:B11) (указано начальное значение экспоненциально сглаженного среднего как среднее значение спроса за исследуемый период), а в ячейке G3 — формула
=(1-$G$12)*G2+$G$12*B2,
которая «протянута» до ячейки G11. Специфика экспоненциального сглаживания позволяет прогнозировать на один период, поэтому прогноз вычисляется только на 11 период по формуле
=(1-$G$12)*G11+$G$12*B11.
Прогнозирование |
Стр. 80 из 164 |
|
J I |
|
J I x y × |
|
|
Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.4 |
II |
|||
|
|
|
|
|
JJ |
Полученные прогнозы можно разделить на два типа (если |
|||||
рассматривать прогноз до 13 периода): оптимистические и пес- |
|||||
симистические. К первым относятся прогнозы на основе абсо- |
|||||
лютных и относительных приростов, а также на основе цепных |
|||||
индексов. Ко второму типу относятся остальные. Такая ситуа- |
|||||
ция возникла неслучайно. Графический анализ исходного ряда |
|||||
показывает, что в первой половине исходного ряда наблюдается |
|||||
тенденция существенного роста, а во второй половине наблю- |
|||||
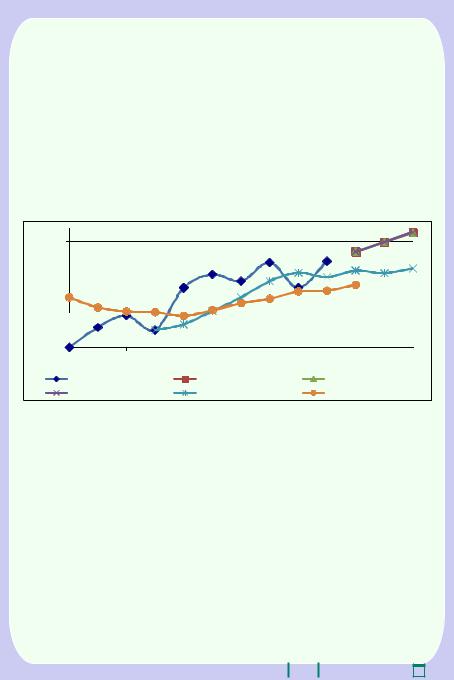
даются колебания около значения 514,5 (рис. 3.1). |
|
|
|||
Рис. 3.1. Прогнозирование спроса различными методами |
|
|
|||
Прогнозирование |
Стр. 81 из 164 |
J I |
J I x y |
× |
|

Оглавление 3.2 Оценка и прогнозирование спроса на . . . |
3.2.4 II |
|
JJ |
Технический анализ графиков исходного временного ряда (объема продаж) и сглаженного с помощью скользящего среднего указывает на возможное изменение тенденции (графики дважды пересекаются). Поэтому прогнозы по линейному тренду, абсолютным и относительным приростам и индексам будут завышенными. Более реалистичным будет прогноз, являющийся средним арифметическим уже полученных прогнозов. Так в 11 периоде прогнозное значение спроса составит:
516,2 + 516,2 + 516,2 + 514,8 + 513,7
5
≈ 515,4.
Расчет прогнозного значения в 12 и 13 периодах уже не может учитывать результаты экспоненциального сглаживания, поэтому среднее прогнозное значение определяется по четырем прогнозам и составляет 516,4 и 517,0 соответственно. В целом и этот прогноз может быть завышен, так как большинство полученных прогнозов являются оптимистическими.
Прогнозирование |
Стр. 82 из 164 |
|
J I |
|
J I x y × |
|
|
