- •Элементарная математика
- •Часть1. (Алгебра и начала анализа)
- •Основные определения
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график. Взаимное расположение графика квадратичной функции и оси абсцисс.
- •Свойства:
- •Взаимное расположение графика квадратичной функции и оси абсцисс.
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства степени. Показательная функция и её свойства.
- •Свойства степени с натуральным показателем
- •Свойства степени с действительным показателем
- •Свойства:
- •Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, степени, частного. Зависимость между логарифмами числа по разным основаниям.
- •Свойства:
- •Преобразование графиков функций
- •Формула корней квадратного уравнения. Теорема Виета. Формула корней квадратного уравнения.
- •Теорема Виета.
- •Разложение квадратного трехчлена на линейные множители
- •Формулы сокращенного умножения.
- •Свойства числовых неравенств.
- •Свойства числовых равенств.
- •Метод интервалов
- •Формулы приведения.
- •Зависимости между тригонометрическими функциями одного и того же аргумента
- •Тригонометрические функции двойного и половинного аргумента
- •Преобразование суммы (разности) в произведение
- •Преобразование произведения в сумму.
- •Обратные тригонометрические функции. (Теорема о корне и теорема об обратной функции)
- •Арксинус
- •Арккосинус
- •Арктангенс
- •Арккотангенс
- •Решение уравнений вида
- •Решение уравнений вида
- •Решение уравнений вида
- •Решение уравнений вида
- •Решение уравнений типа с помощью вспомогательного аргумента.
- •Признаки делимости на 2,3,5,9,10.
- •Делимость на 2
- •Делимость на 3 на 9
- •Делимость на 5
- •Делимость на 10
- •Квадратный корень из числа. Арифметический квадратный корень, его свойства. Корень и арифметический корень п-ой степени
- •Свойства арифметического квадратного корня
- •Cвойства
- •Геометрическая прогрессия. Формулы п-го члена и суммы п первых членов геометрической прогрессии. Характеристическое свойство геометрической прогрессии.
- •Тригонометрическая окружность
- •Сборник формул
- •Библиографический список
М.Л. Шалагинова
Элементарная математика
Часть1. (Алгебра и начала анализа)
Учебное пособие для студентов
математических специальностей
Киров, 2012
Оглавление
Основные определения
О.
Функцией
называется такая зависимость переменной
![]() от переменной
от переменной![]() ,
при которой каждому значению переменной
,
при которой каждому значению переменной![]() соответствует единственное значение
переменной
соответствует единственное значение
переменной![]() .
.
О.
Переменную
![]() при этом называют независимой переменной
илиаргументом,
а переменную
при этом называют независимой переменной
илиаргументом,
а переменную
![]() при этом называют зависимой переменной
илифункцией.
при этом называют зависимой переменной
илифункцией.
О. Множество всех значений аргумента называется областью определения функции.
О. Множество всех значений, которые принимает зависимая переменна (функция) называется множеством значений функции.
О.
Функция
называется периодической
![]() ,
при этом числоT
– называется периодом
функции.
,
при этом числоT
– называется периодом
функции.
О. Функция называется чётной, если выполняются следующие условия:

О. Функция называется нечётной, если выполняются следующие условия:

О. Функция называется возрастающей, если выполняется следующее условие:
![]()
О. Функция называется убывающей, если выполняется следующее условие:
![]()
О.
![]() называется
наименьшим
значением функции
называется
наименьшим
значением функции
![]() ,
если выполняется следующее условие:
,
если выполняется следующее условие:
![]()
О.
![]() называется
наибольшим
значением функции
называется
наибольшим
значением функции
![]() ,
если выполняется следующее условие:
,
если выполняется следующее условие:
![]()
О.
Графиком
функции
называется подмножество координатной
плоскости, состоящее из точек с
координатами![]() ,
где
,
где![]()
О.
Прямая
![]() называетсягоризонтальной
асимптотой графика
функции,
если
называетсягоризонтальной
асимптотой графика
функции,
если
![]()
О.
Прямая
![]() называетсявертикальной
асимптотой графика
функции,
если
называетсявертикальной
асимптотой графика
функции,
если
![]()
О.
Прямая
![]() называетсянаклонной
асимптотой графика
функции,
если
существуют конечные пределы:
называетсянаклонной
асимптотой графика
функции,
если
существуют конечные пределы:
![]() и
и![]()
Свойства функции и её график
О.
Функция
вида:![]() ,
где
,
где![]() называетсялинейной
функцией.
называетсялинейной
функцией.
Свойства:
Область определения функции
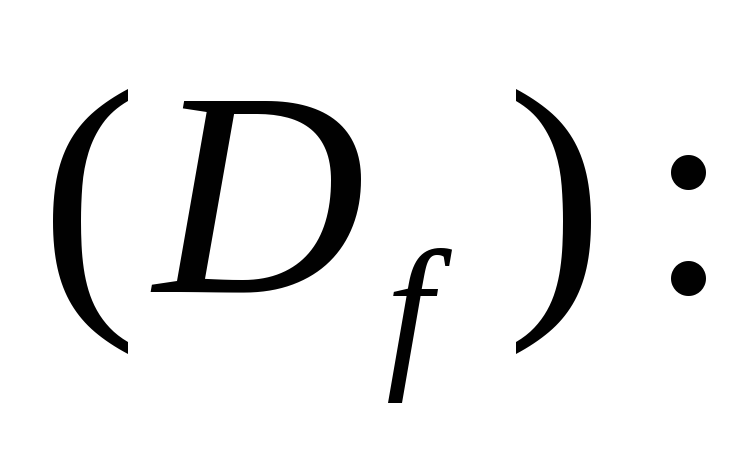
![]() ,
т.к. значение выражения
,
т.к. значение выражения
![]() однозначно определяется
однозначно определяется![]() (почему?).
(почему?).
Множество значений функции:
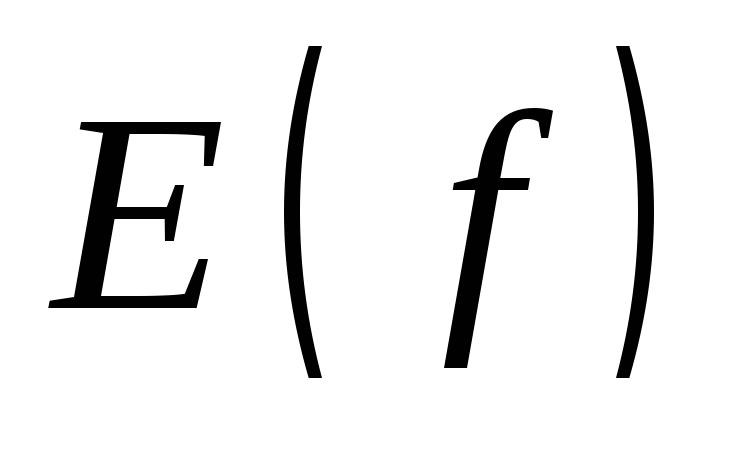
Если
![]() ,
то множество значений состоит из одного
числаb,
,
то множество значений состоит из одного
числаb,
![]() ,
т.к. значение выражения
,
т.к. значение выражения![]() в этом случае равно
b.
в этом случае равно
b.
Если
![]() ,
то множеством значений функции будет
множество
,
то множеством значений функции будет
множество![]() ,
т.к.
,
т.к.![]() .
.
Периодичность:
Теорема.
Если
![]() ,
то функция является периодической и её
период – любое действительное число.
,
то функция является периодической и её
период – любое действительное число.
Если
![]() ,
то функция не является периодической.
,
то функция не является периодической.
Доказательство:
При
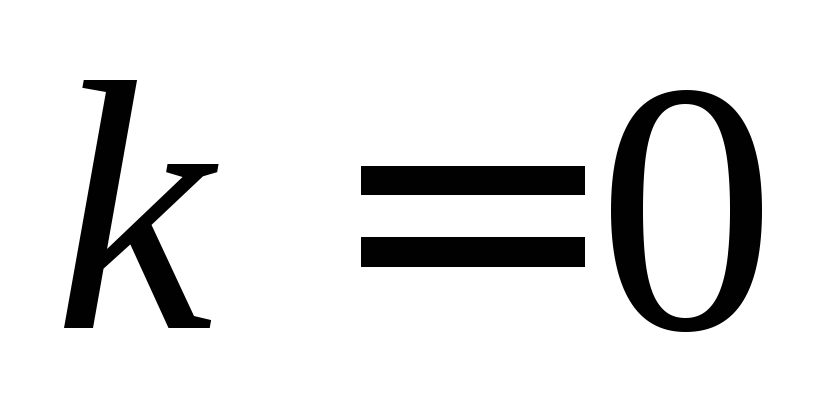 утверждение верно, т.к. функция при всех
значенияхх
принимает одно значение, равное b.
утверждение верно, т.к. функция при всех
значенияхх
принимает одно значение, равное b.Пусть
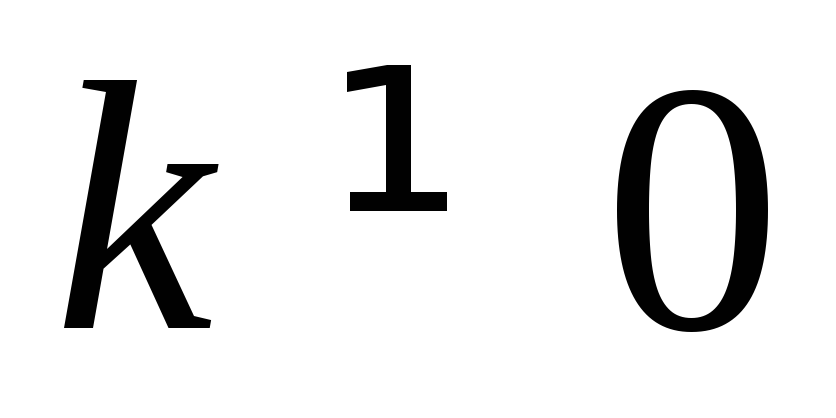 ,
предположим, что линейная функция имеет
период
,
предположим, что линейная функция имеет
период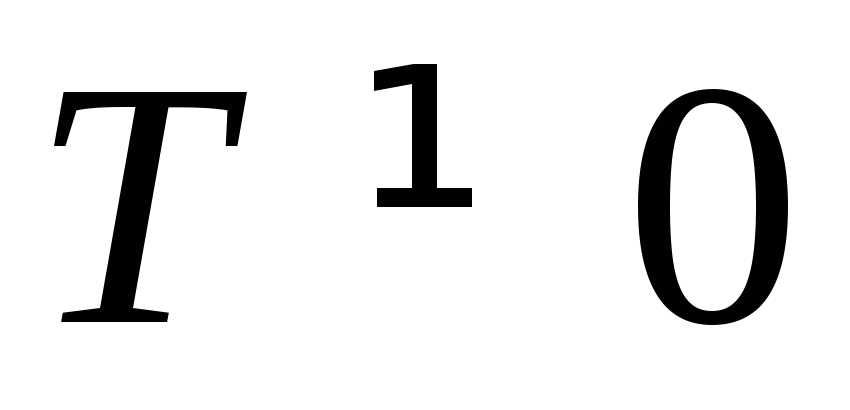 ,
т.е.
,
т.е.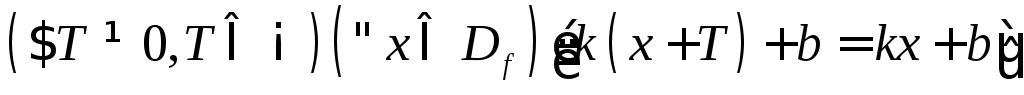
![]() ,
т.к. по условию
,
т.к. по условию
![]() ,
значит предположение о том, что линейная
функция имеет период
,
значит предположение о том, что линейная
функция имеет период![]() ,
не верно, и при
,
не верно, и при![]() линейная функция не является периодической.
линейная функция не является периодической.
Чётность/нечётность
Если
![]() ,
то функция не является ни чётной, ни
нечётной, т.к.
,
то функция не является ни чётной, ни
нечётной, т.к.
![]() ,
а
,
а
![]() и
и![]()
Если
![]() ,
то функция имеет вид:
,
то функция имеет вид:![]() ,
и
,
и![]()
![]() ,
значит, функция является чётной.
,
значит, функция является чётной.
Если
![]() ,
то функция имеет вид:
,
то функция имеет вид:![]() ,
и
,
и![]() ,
значит, функция является нечётной.
,
значит, функция является нечётной.
Точки пересечения графика с осями координат.
Точки
пересечения с осью
![]() если
если![]()
![]()
Точки
пересечения с осью
![]()
Тогда
если
![]()
Если
![]()
Если
![]()
Если
![]()
Промежутки знакопостоянства функции (промежутки, на которых функция сохраняет свой знак):
если
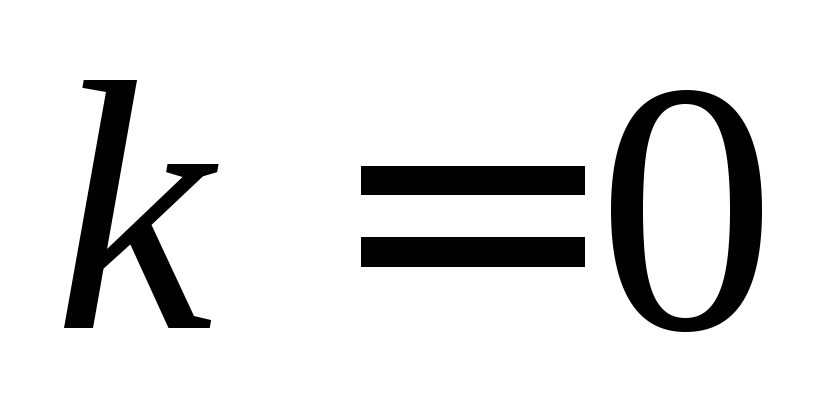 ,
то
,
то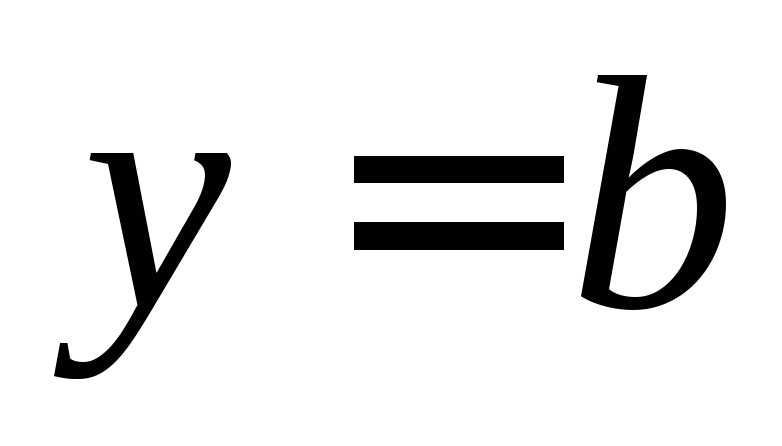 ,
значит, функция не меняет своего знака
на всей области определения: если
,
значит, функция не меняет своего знака
на всей области определения: если ,
если
,
если
если
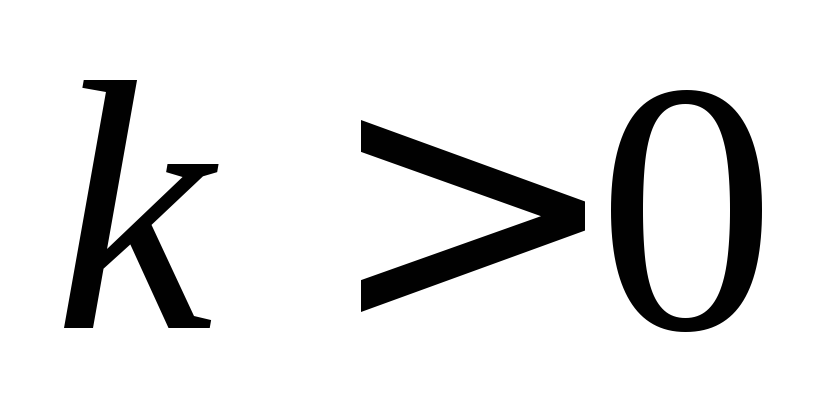 ,
то
,
то
![]()
![]()
![]() :
:
![]()
если
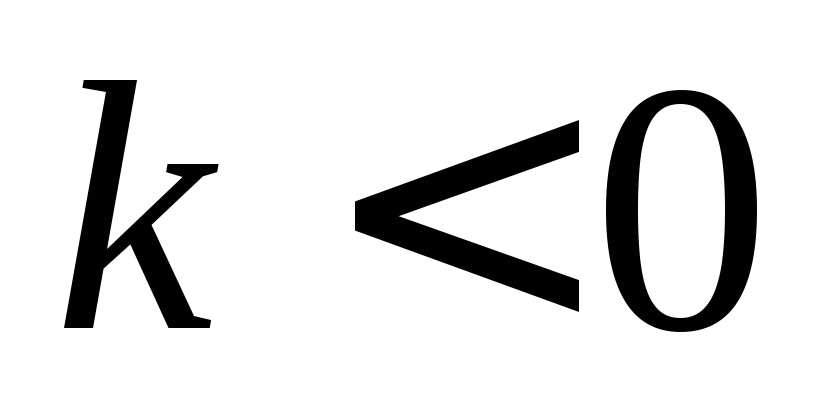 ,
то
,
то
![]()
![]()
![]() :
:
![]()
Промежутки монотонности (Интервалы возрастания/убывания функции)
Теорема.
Если
![]() ,
то функция
,
то функция![]() - постоянное число (b=const),
- постоянное число (b=const),
Если
![]() то функция возрастает,
то функция возрастает,
Если
![]() ,
то функция убывает.
,
то функция убывает.
Доказательство:
Возьмем
произвольные
![]() такие, что
такие, что![]() и рассмотрим разность:
и рассмотрим разность:![]()
если
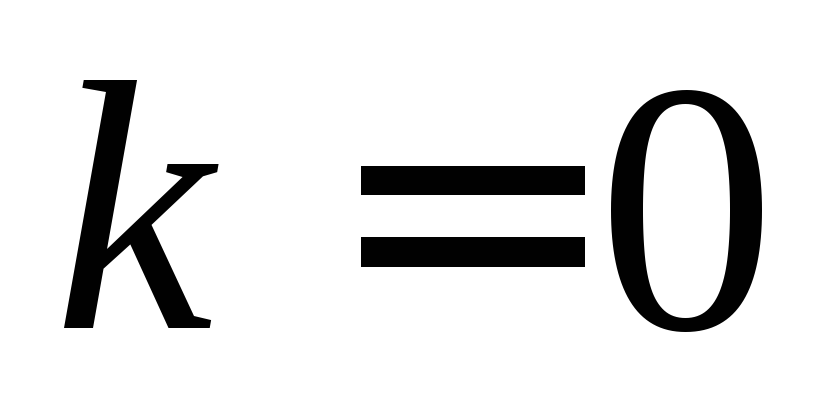 ,
то
,
то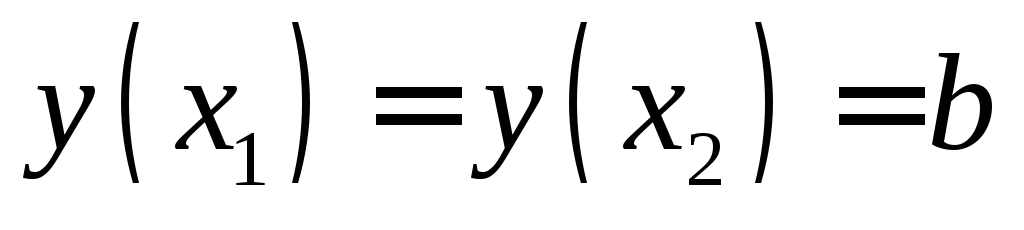 -
функция постоянна
-
функция постояннаесли
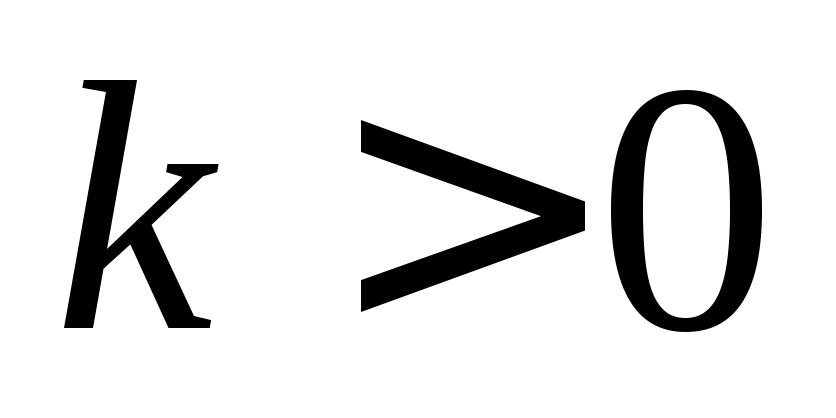 ,
то
,
то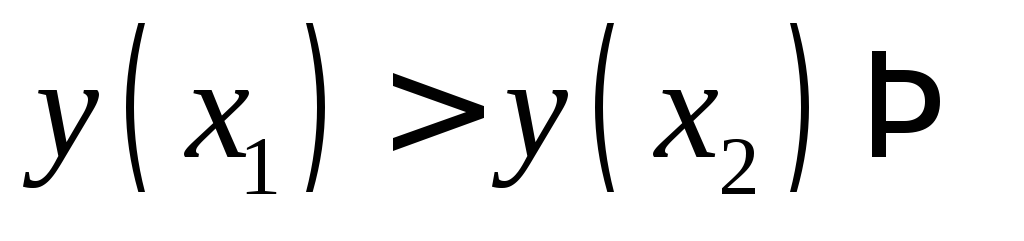 функция возрастает
функция возрастаетесли
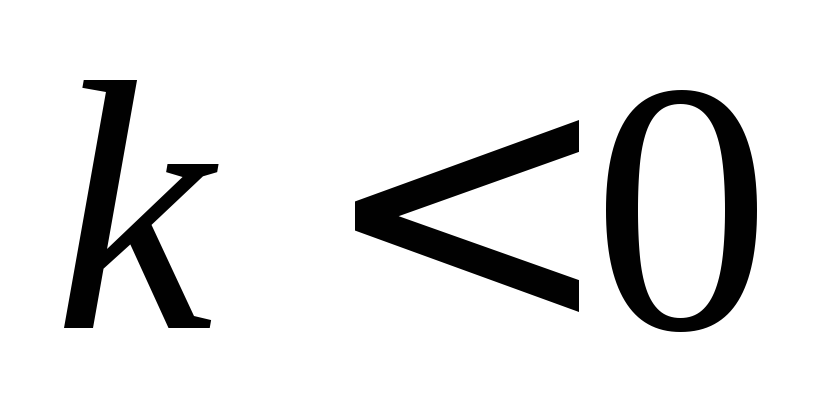 ,
то
,
то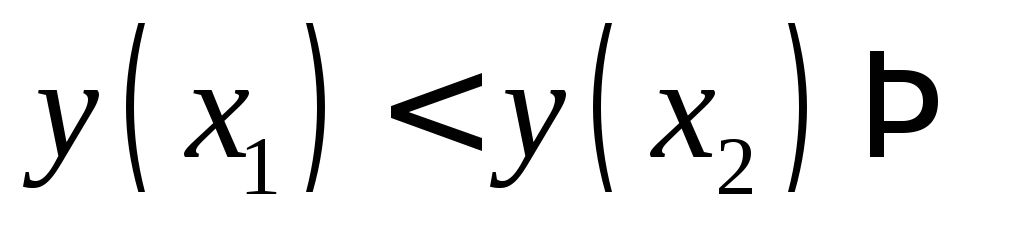 функция
убывает
функция
убывает
Наибольшее/наименьшее значение функции
Функция
![]() не имеет наименьшего и наибольшего
значения, т.к. её множеством значений
является всё множество
не имеет наименьшего и наибольшего
значения, т.к. её множеством значений
является всё множество![]() .
.
График функции
Графиком линейной функции является прямая (рис 1).