23. Тригонометрические функции двойного и половинного аргумента

Формулы сложения позволяют выразить ,ичерез тригонометрические функции угла.

Рассмотрим формулы:

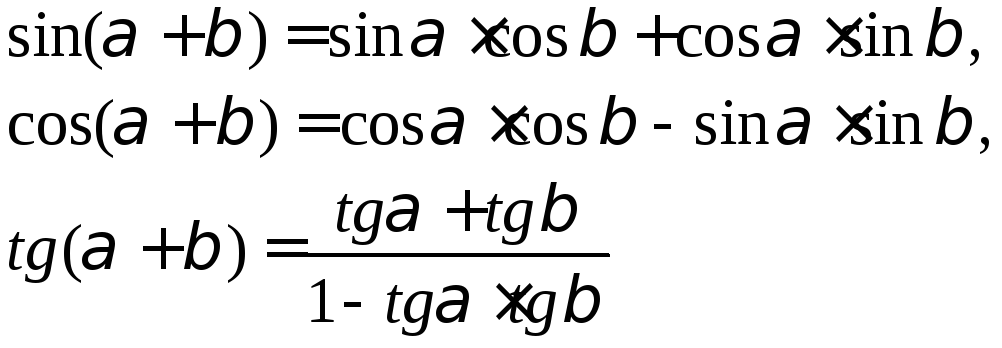
Положим в этих формулах равным.Получим:

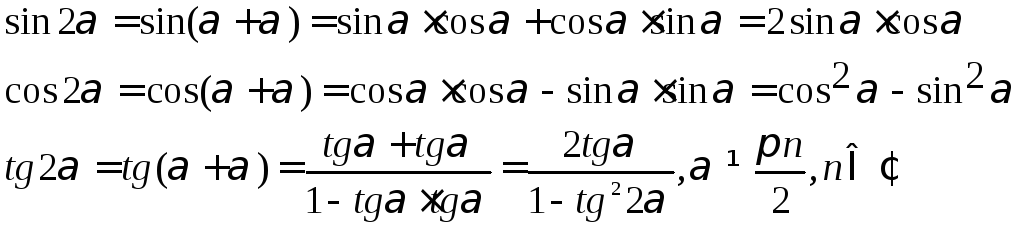
Полученные формулы: 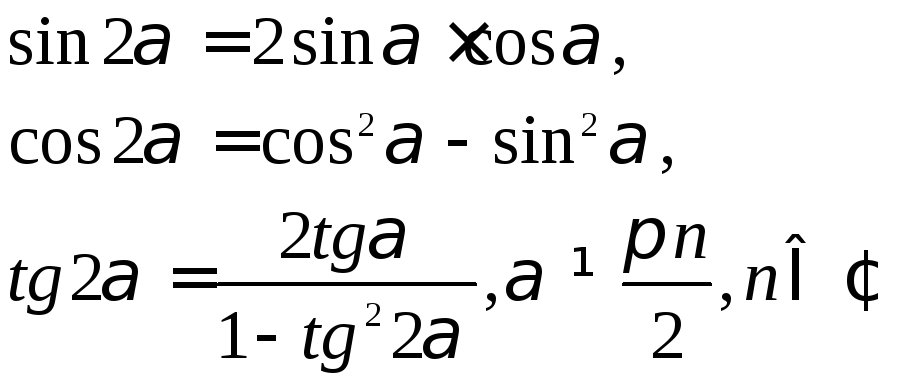называютформулами двойного угла.

Замечание.Воспользовавшись основным тригонометрическим тождеством, формулу косинуса двойного угла можно переписать в виде

.

Из формул двойного аргумента легко выводятся формулы половинного аргумента:

,

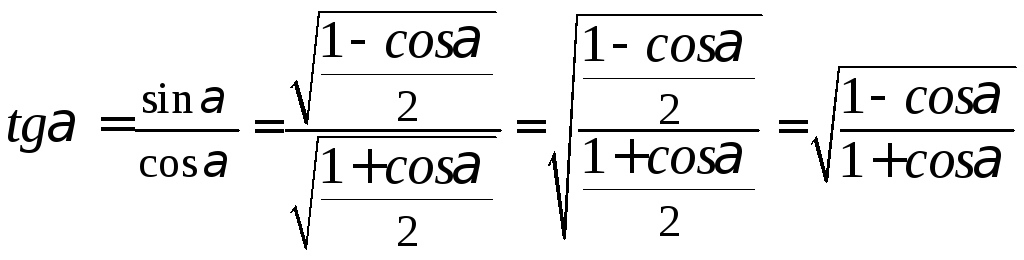и

24. 

Рассмотрим тригонометрическую окружность. Повернем радиус , равный, около точкина уголи на угол. Получим радиусыи.

Найдем скалярное произведение векторов и

Пусть координаты точки равны, координаты точкиравны. Эти же координаты имеют соответственно и векторыи.

По определению скалярного произведения векторов:

Выразим скалярное произведение ичерез тригонометрические функции углови. Из определения косинуса и синуса следует, что

Подставив значения в правую часть равенства, получим

С другой стороны, по теореме о скалярном произведении векторов, имеем:

.

Угол BOCмежду векторамииможет быть равенили, либо может отличаться от этих значений на целое число оборотов.

В любом из этих случаев, так как

Поэтому

Из равенств иследует:

,

Поделив обе части равенства на , получаем

С помощью формулы легко получить следующую формулу

Так как

Поделим числитель и знаменатель на , получим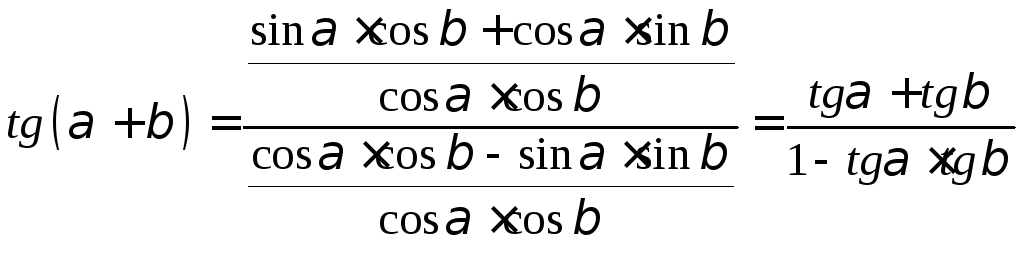

Поделим числитель и знаменатель на , получим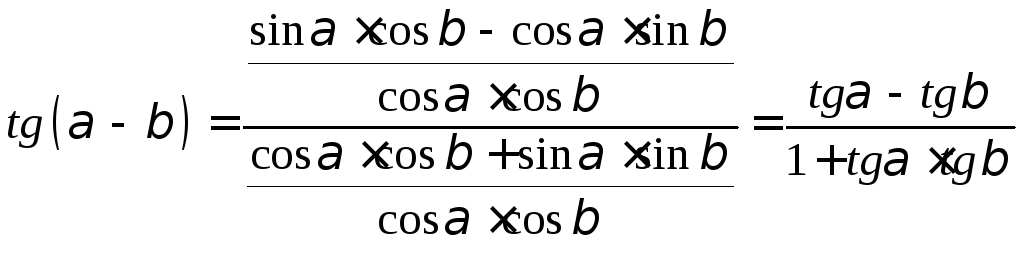

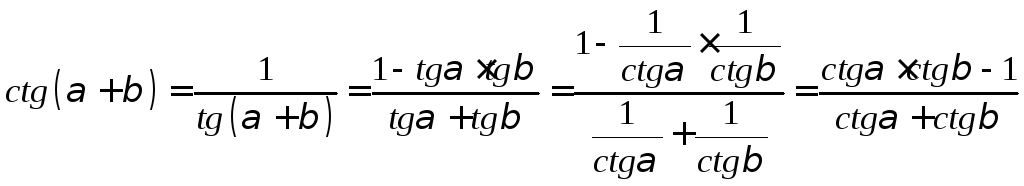
Аналогично для (проведите доказательство самостоятельно)

25. Преобразование суммы (разности) в произведение

Сумму и разность синусов или косинусов можно представить в виде произведения тригонометрических функций.

Чтобы представить в виде произведения сумму , положимии воспользуемся формулами синуса суммы и синуса разности. Получим:

Решая систему , получаем, чтои, таким образом.

Аналогично, можно вывести формулы разности синусов, суммы и разности косинусов.

26. Преобразование произведения в сумму.

Произведение ;;можно представить в виде суммы тригонометрических функций.

Положим и,

отсюда, решив систему: , получаем,и

Воспользуемся формулами преобразования суммы в произведение:

27. Обратные тригонометрические функции. (Теорема о корне и теорема об обратной функции)

Теорема о корне:

Пусть функция возрастает (убывает) на промежутке, число– любое из значений, принимаемых функциейна этом промежутке. Тогда уравнениеимеет единственный корень в промежутке.

Теорема об обратной функции:

Если функция возрастает (убывает) на промежутке, то она обратима и обратная к ней функция, определённая на множестве значений функции, так же является возрастающей (убывающей).

Арксинус

О.Функциявозрастает наи принимает все значения отдо, значит по теореме о корнев промежуткеуравнениеимеет единственный корень.

Это число называетсяарксинусомчислаи обозначается.

Т.е. арксинусомчисланазывается такое число из промежутка, синус которого равен: .

Т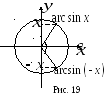ак как функцияна промежуткестрого возрастает, значит, по теореме об обратной функции, она имеет обратную функцию:, переобозначив переменные, получаем

Рассмотрим свойстваэтой функции:

1. Область определения функции:

.

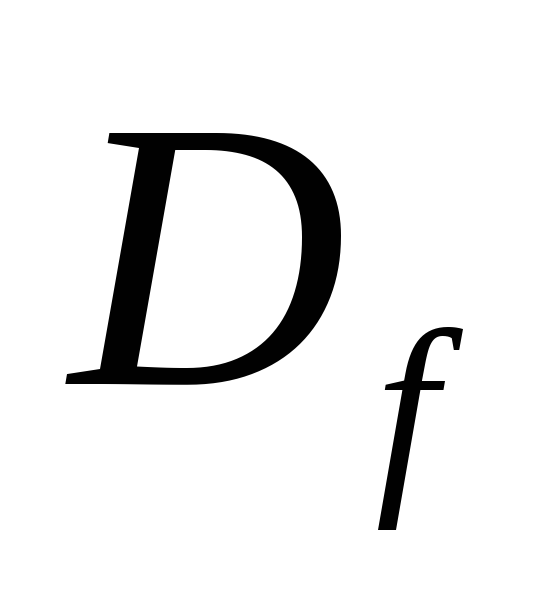
2. Множество значений функции:

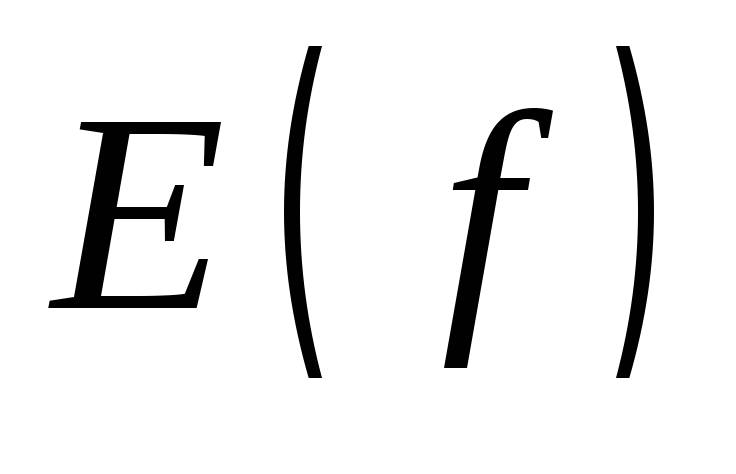
3. Периодичность:

Функция не периодическая, так как она строго возрастает на всей области определения (по теореме об обратной функции)

4. Чётность/нечётность

Из рисунка 19 видно, что , т.е. функциянечетная

5. Точки пересечения графика с осями координат.

С осью : если

С осью

6. Промежутки знакопостоянства функции:

:

7. Интервалы возрастания/убывания

П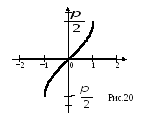о теореме об обратной функции, так как функциявозрастает на,

следовательно возрастает на.

8. Наибольшее/наименьшее значение функции

Так как функция строго возрастает на всей области определения и непрерывна, то

9. График функции

(рис 20).