39

Лекция 4

Методы расчета однозвенных полнодоступных включений по системе с ожиданием

Экспоненциальное время обслуживания. Вторая формула Эрланга

Задано:

1.Поток вызовов – простейший, время обслуживания случайное, распределенное по экспоненциальному закону.

2.Коммутационная схема – однозвенная, в выходы которой включен полнодоступный пучок линий.

Дисциплина обслуживания - с ожиданием, вызовы из очереди обслуживаются в порядке их поступления.

Требуется найти вероятность того, что система будет находиться в i-ом состоянии Р_i. При i ≤ V Р_i есть вероятность занятости i линий из V. При i < V Р_i есть вероятность того, что все V линий заняты и i-V вызовов ожидают обслуживания.

Число вызовов, находящихся в системе, может быть больше числа обслуживающих устройств i ≥V.

Поэтому вероятность P_i определяется для двух случаев:

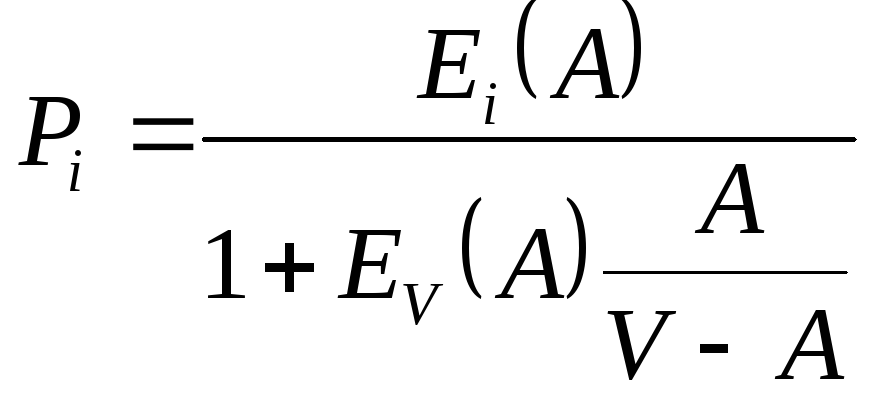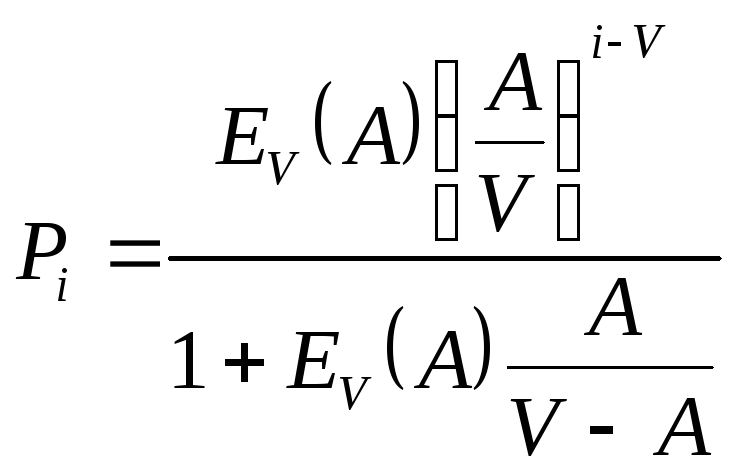, 0 ≤i ≤ V

i ≥ V.

Это распределение Эрланга для систем с ожиданием.

Определим вероятность того, что поступивший в произвольный момент времени вызов найдет все линии занятыми, или, что то же самое, вероятность того, что временя ожидания γ больше нуля (вторая формула Эрланга)

вторая формула Эрланга.

Эта формула определяет вероятность ожидания. С другой стороны ее можно рассматривать как долю вызовов, задержанных при обслуживании, но не потерянных. Поэтому эту вероятность называют условными потерями, а систему обслуживания – с условными потерями.

При фиксированных А и V вероятность условных потерь больше, чем вероятность явных потерь.

Вероятность того, что для поступившего в произвольный момент времени вызова ожидание будет больше t, определяется по формуле

где

- время ожидания нормируется относительно средней длительности занятия.

Это выражение определяет закон распределения времени ожидания и так же является второй формулой Эрланга.

Кроме величин P(γ>0) и P(γ>t) для характеристики систем с ожиданием используются следующие показатели.

Среднее время ожидания по отношению ко всем поступившим вызовам

Среднее время ожидания для ожидающих вызовов

Вероятность наличия в очереди хотя бы одного вызова

Средняя длина очереди или число задержанных вызовов

Графические зависимости между основными величинами, входящими во вторую формулу Эрланга

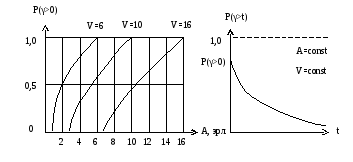
При А≥ V P(γ>0)=1 и имеет место бесконечная очередь.

А,Эрл.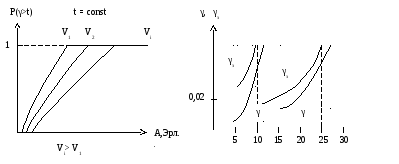

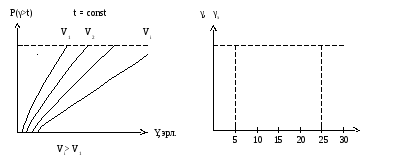
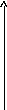
Данные зависимости строятся при измерении времени ожидания в единицах средней длительности занятия линий или приборов. В этом случае одним и тем же графиком можно пользоваться для процессов, которые не соизмеримы в реальном масштабе времени.

Зависимости V= f(А) при P=const и P = f(А) при V= const для систем с ожиданием имеют точно такой же характер, как и для систем с явными потерями. Однако количественные оценки этих зависимостей существенно различаются. При заданных потерях величина поступающей нагрузки в системах с ожиданием должна быть меньше, чем в системах с потерями. При одних и тех же значениях потерь обслуженная нагрузка в системах с потерями больше, чем в системах с ожиданием. Таким образом, системы с потерями обладают более высокой пропускной способностью, чем системы с ожиданием.

Где же системы с ожиданием находят практическое применение?

При малых потерях, исчисляемых несколькими промилями или даже процентами, абонент не ощущает неудобства в обслуживании. Поэтому в области малых потерь предпочтительнее система с потерями, обладающая более высокой пропускной способностью

При больших потерях системы с потерями не обеспечивают должного качества обслуживания и непригодны для применения.

В случае больших потерь нельзя однозначно дать оценку системам с ожиданием. Необходимо, чтобы время ожидания начала обслуживания не вызывало неудобства у абонентов.

Системы с ожиданием следует применять в случае больших потерь, если возможно обеспечить мало ощутимое для абонентов время ожидания.

При практических расчетах систем с ожиданием используют номограммы. Наиболее полно они представлены в книге Захаров Г.П., Варакосин Н.П. Расчет количества каналов связи при обслуживании с ожиданием. - М.: Связь, 1967. - 194с.

Системы с ожиданием при постоянной длительности занятия. Кривые Кроммелина и Бёрке

Задано:

1.Поток вызовов – простейший, длительность обслуживания постоянна и равна h.

2.Коммутационная схема – однозвенная, способ включения линий на выходе - полнодоступный.

3.Дисциплина обслуживания – с ожиданием, вызовы, находящиеся на ожидании, обслуживаются в порядке их поступления.

Требуется определить функцию распределения длительности ожидания начала обслуживания для любого вызова P(γ>t).

К таким системам относятся управляющие устройства координатных и электронных систем коммутации. Исследование таких систем выполнено Кроммелином для случая, когда вызовы обслуживаются в порядке поступления, и Бёрке – если вызовы обслуживаются в случайном порядке.

Обозначим:

допустимое время ожидания, нормированное относительно h.

V=1,2,…. число обслуживающих устройств (маркеров, процессоров).

удельная нагрузка на одно обслуживающее устройство.

При практических расчетах используются соответствующие кривые Кроммелина и Бёрке.

P(γ>t)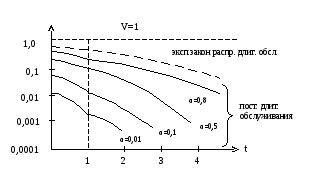

Кривые показывают, что характер зависимостей P(γ>t)=f(t) такой же, как и при экспоненциальном распределении длительности обслуживания. С увеличением времени ожидания γ сверх заданного времени t вероятность P(γ>t) уменьшается. Однако количественные оценки существенно различаются. Для систем с постоянным временем обслуживания вероятность ожидания меньше, чем при экспоненциальном, или время ожидания существенно меньше.

V=1

P(γ>t)

1,0

10^-1

10^-2

10^-3

1 2 3 4 5 6 7 8 9 10 t

В автоматических системах коммутации наибольшее распространение нашли системы с ожиданием, в которых обслуживание ожидающих вызовов осуществляется при случайном выборе из очереди. Распределение времени ожидания P(γ>t)=f(t) в таких системах приводится на графике (сплошные линии). Для сравнения пунктирными линиями показано распределение при обслуживании вызовов в порядке очереди.

Из графиков видно, что для небольших значений t качественные характеристики обслуживания выше при случайном выборе из очереди. Именно эта область значений t представляет интерес для существующих систем коммутации. При больших значениях t вероятность P(γ>t) при случайном выборе из очереди существенно превышает соответствующие значения вероятностей при обслуживании вызовов в порядке их поступления.

Постоянная длительность занятия управляющих устройств, а главное ее малое значение, позволяет устанавливать большое значение вероятности условных потерь P(γ>0). При этом величина P(γ>t) при относительно больших t оказывается величиной очень малой и одновременно допустимое ожидание имеет небольшое значение, неощутимое источником вызова.

Все это приводит к целесообразности использования для управляющих устройств дисциплины обслуживания с ожиданием.

Контрольные вопросы

1. Перечислите основные элементы математической модели, положенной в основу второй формулы Эрланга.

2. Запишите вторую формулу Эрланга. От каких параметров зависит величина условных потерь?

3. Что определяет вероятность Р( γ > 0 ) ?

4. Каково соотношение между вероятностями явных и условных потерь?

5. Запишите формулу функции распределения времени ожидания при случайном времени занятия.

6. Какие характеристики используются для оценки систем с ожиданием?

7. Каков характер зависимости Р( γ > 0 ) от поступающей нагрузки при фиксированном значении емкости пучка линий?

8. Каков характер закона распределения времени ожидания?

9. Сравните пропускную способность систем с ожиданием и с явными потерями.

10. Чем отличаются математические модели второй формулы Эрланга и теории Кроммелина?

11. В чем разница в процессе обслуживания вызовов для моделей Кроммелина и Берке?

12. Какова область применения систем с ожиданием?