56курсы / 5 курс / 10 / Теория телетрафика / Лекция 3

30

Лекция 3

Методы расчета однозвенных полнодоступных включений по системе с потерями

Обслуживание простейшего потока. Первая формула Эрланга.

Мы уже отмечали, что математическая модель системы распределения информации характеризуется тремя основными элементами: потоком вызовов, схемой коммутационной системы и дисциплиной обслуживания.

В данном разделе мы рассматриваем простейшую модель.

Задано:

1.Поток вызовов – простейший с параметром λ.

2.Коммутационная схема – однозвенная, в выходы которой включен полнодоступный пучок. Это означает, что любой вход коммутационной схемы может быть подключен к любому выходу, причем подключение входа к выходу осуществляется в одной точке коммутации.

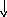Входы

Выходы

3.В качестве дисциплины обслуживания примем обслуживание вызовов с явными потерями.

Требуется найти вероятность занятия i любых линий из общего числа V в фиксированный момент времени t.

Эта вероятность определяется из распределения Эрланга

Для простейшего потока λt=A и распределение Эрланга может быть записано в виде:

E_i,v(A) – это вероятность того, что в произвольный момент времени в полнодоступном пучке емкостью V линий, на который поступает интенсивность нагрузки A, создаваемая простейшим потоком, занято i любых линий.

Вероятность того, что в полнодоступном пучке заняты все V линий (i=V), равна:

Первая формула Эрланга.

Качество обслуживания вызовов можно оценить:

1.Вероятностью потерь по вызовам .

2.Вероятностью потерь по нагрузке .

3.Вероятностью потерь по времени, которая определяется как доля времени, в течение которого заняты все линии - P_t.

В самом общем случае имеет место соотношение

P_н ≤ P_в ≤ P_t .

P_в ≤ P_t , т.к. может быть такой случай, когда все линии заняты, а вызов не поступает.

P_н ≤ P_в , т.к. длительность занятия повторными вызовами может быть значительно меньше средней длительности занятия.

Доказано, что в полнодоступном пучке, на который поступает простейший поток вызовов

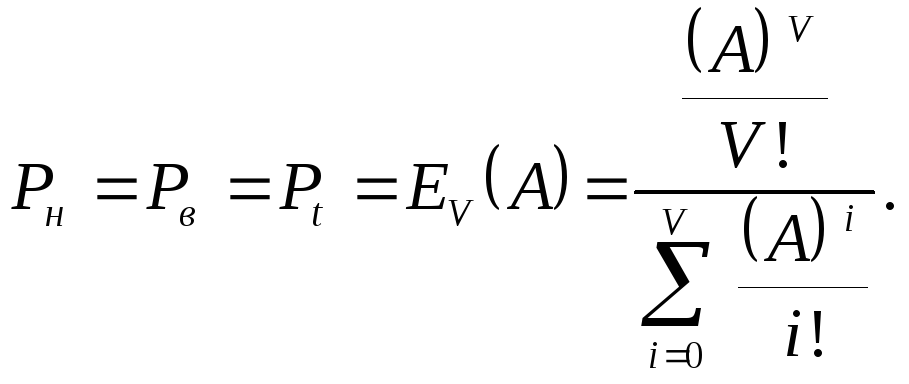
Первая формула Эрланга табулирована. Впервые эти таблицы были составлены К.Пальмом и получили название таблиц Пальма. Уточнение этих таблиц выполнено Г.П.Башариным.

Графические зависимости между параметрами первой формулы Эрланга

Потери являются функцией двух переменных P = E_V (A) =f (V,A)

Практический интерес представляет область малых потерь 0,001÷ 0,01

Интенсивность поступающей нагрузки изменилась с 32,5Эрл. до 37,9Эрл., т.е. на 17%, а потери возросли в 10 раз.

На практике приходится решать задачу определения числа линий по нагрузке при заданной величине потерь. Число линий из первой формулы Эрланга в явном виде не выражается. Решить задачу можно подбором.

V

70 P=0,001

60 P=0,01

50

40

30

20

10

0

10 20 30 40 50 А, эрл.

При P=const в достаточно большом интервале изменения нагрузки при А > 10Эрл число линий приближенно можно определять из выражения V= αА + β, где α, β – коэффициенты, зависящие от величины потерь.

Средняя интенсивность нагрузки, обслуженной одной линией полнодоступного пучка, определится

Записывая выражения для E_V(А) и E_V-1 (А) можно убедиться, что

E_V (А)=

Подставляя А в выражение для Y₀, получим

.

Тогда

При малой величине потерь

Из этих графиков можно сделать вывод: для повышения использования линий в пучках необходимо укрупнять пучки. Эффект от объединения пучков тем выше, чем меньше их емкость. При V > 100 приращение пропускной способности незначительно.

При V → ∞ формула Эрланга может быть заменена формулой Пуассона.

E_V (А) =

Формула Эрланга E_i,V(А) позволяет вычислить вероятность занятия i любых линий в пучке из V линий. Часто требуется определить вероятность занятия определенных (фиксированных) линий i из общего числа V. Эта вероятность, как показал К.Пальм, определяется из выражения

Рассмотрим пример.

1 1

2 2

N=10 V

Пусть N = 10 источников создают интенсивность нагрузки А =5Эрл. Чтобы обеспечить потери 0,005 по первой формуле Эрланга требуется V = 12 линий. Но в такой схеме одновременно может быть занято только 10 линий. Этот парадокс объясняется тем, что первая формула Эрланга использована для не простейшего потока (число источников N < 100).

Форма таблиц Пальма

	11	12
5,0	008287	003441
5,1	009332	003950

Обслуживание потока от ограниченного числа источников нагрузки. Формула Энгсета.

Задано:

1.Поток вызовов – примитивный.

2.Коммутационная схема – однозвенная, в выходы которой включен полнодоступный пучок линий.

3.Дисциплина обслуживания – с явными потерями.

Требуется найти вероятность занятия i любых линий из общего пучка V в фиксированный момент времени.

Для примитивного потока параметр потока λ зависит от числа вызовов, находящихся на обслуживании, т.е. λ = (N-i)α, где N- число источников, i–число занятых источников, α –параметр потока от одного источника в свободном состоянии.

Вероятность занятия i любых линий из общего числа линий V для примитивного потока определяется по формуле Энгсета.

Потери по времени по определению представляют собой долю времени, в течение которого заняты все V линий

Для модели Энгсета потери по нагрузке, вызовам и времени не равны:

P_н < P_в < P_t .

При практических расчетах удобнее пользоваться не параметром свободного источника α, а интенсивностью нагрузки от одного источника а

Тогда формулы Энгсета перепишутся в виде

При N → ∞ эти формулы переходят в формулу Эрланга, а при N→ ∞ и

V→ ∞ - в формулу Пуассона.

Формула Энгсета потерь по вызовам табулирована: Лившиц Б.С., Фидлин Я.В. "Системы массового обслуживания с конечным числом источников нагрузки" Связь, 1968. 167c.

Форма таблиц

a= 0,075 Эрл.

	61	62
4	3709327	3776984
5	2519712	2587737

P_в=0,2587737 при N=62, V=5, a=0,075

Сравнение пропускной способности коммутационной системы при обслуживании примитивного и простейшего потоков.

При построении этого графика нагрузка А=Na от N источников принята равной нагрузке А, создаваемой простейшим потоком при E_V(А)=const=0,005.

Из этих графиков можно сделать следующие выводы:

1.С увеличением N при одной и той же величине Na пропускная способность полнодоступного пучка при обслуживании примитивного потока приближается к пропускной способности при обслуживании простейшего потока. Чем меньше емкость полнодоступного пучка, тем меньше указанное различие.

2.С возрастанием Na увеличивается пропускная способность при обслуживании примитивного потока по сравнению с простейшим.

Это объясняется тем, что для примитивного потока параметр потока от одного источника в момент его свободности равен α, а в момент занятости - нулю. Для простейшего потока параметр считается равным α вне зависимости от занятости или свободности источника.

В практических расчетах формулой Эрланга пользуются при N ≥ 100 , при N < 100 – формулой Энгсета.

1 1 1

2 2 2

N=10 V

По первой формуле Эрланга V=12, по формуле Энгсета V=9.

Контрольные вопросы

1. Перечислите основные элементы математической модели, положенной в основу первой формулы Эрланга.

2. Запишите формулу Эрланга для определения вероятности того, что в полнодоступном пучке линий, обслуживающем простейший поток вызовов, занято i любых линий.

3. Приведите первую формулу Эрланга.

4. Каково соотношение между потерями по вызовам, нагрузке и времени для модели первой формулы Эрланга?

5. Покажите характер зависимости между параметрами первой формулы Эрланга.

6. Запишите формулу, определяющую величину обслуженной нагрузки полнодоступным пучком линий, на который поступает простейший поток вызовов.

7. Запишите формулу, определяющую величину потерянной нагрузки полнодоступным пучком линий, на который поступает простейший поток вызовов.

8. Запишите формулу для определения средней интенсивности нагрузки, обслуженной одной линией полнодоступного пучка, на который поступает простейший поток вызовов.

9. Покажите характер зависимости среднего использования одной линии полнодоступного пучка от интенсивности поступающей нагрузки, на который поступает простейший поток вызовов.

10. Каково влияние емкости полнодоступных пучков на пропускную способность этих пучков?

11. Каково влияние потерь на пропускную способность полнодоступных пучков?

12. Каково соотношение между потерями по вызовам, нагрузке и времени для модели первой формулы Энгсета?

13. Чем отличаются математические модели Эрланга и Энгсета?

14. Сравните пропускную способность полнодоступного пучка, обслуживающего вызовы примитивного и простейшего потоков вызовов.

15. Что позволяют определить таблицы Пальма?